基于自由振動衰減響應的硬涂層材料力學特性參數辨識

孫 偉， 王 茁

(東北大學 機械工程與自動化學院，沈陽 110819)

基于自由振動衰減響應的硬涂層材料力學特性參數辨識

孫 偉， 王 茁

(東北大學 機械工程與自動化學院，沈陽 110819)

獲得硬涂層材料的儲能模量和損耗因子等力學特性參數是硬涂層復合結構建模及減振優化設計的基礎。現有的關于硬涂層材料參數辨識研究通常是基于梁形試件和復雜的實驗過程。而這里面向懸臂板結構，提出一種僅需測得涂層前后懸臂板的時域共振自由振動衰減響應，來辨識硬涂層材料力學特性參數的方法。首先，確定了由自由振動衰減響應辨識硬涂層儲能模量及損耗因子的原理。進一步，給出了獲得上述硬涂層材料參數所需的關鍵參數(包括響應包絡線、即時共振頻率和阻尼)的辨識方法。再則，描述了硬涂層板有限元建模以及共振頻率、模態應變能和參考應變的求解方法。最后以涂敷NiCoCrAlY+YSZ硬涂層的懸臂薄板為例進行了實例研究，獲得了該混合涂層的儲能模量及損耗因子。進一步，將獲得的硬涂層材料參數代入到有限元分析模型，通過對比試驗與有限元計算獲得的硬涂層板前6階共振頻率，證明了所辨識的材料參數的合理性。經比較發現，辨識獲得的硬涂層儲能模量及損耗因子隨參考應變的變化規律同其他文獻基本一致，但該結果可直接用于硬涂層板形結構的建模。

自由振動衰減響應；硬涂層；力學特性參數；參數辨識

硬涂層是指由金屬基、陶瓷基或兩者的混合制成的涂層材料，目前主要用于熱障、抗摩擦和抗腐蝕。近年來的研究發現，硬涂層可以在高溫、高腐蝕環境下降低薄殼構件的振動應力，因而硬涂層阻尼減振研究受到了越來越廣泛關注[1-3]。進一步的研究發現，硬涂層之所以能減振是源于硬涂層顆粒之間的內摩擦，TASSINI[4]，TORVIK[5],AL-RUB[6]等分別創建了微觀材料學表征模型來解釋硬涂層的減振機理。為了更好地實施硬涂層阻尼減振，還需要創建宏觀的硬涂層復合結構的動力學分析模型，基于該分析模型來實現對硬涂層減振性能的有效預估與設計。而創建這樣的模型的關鍵是獲得硬涂層材料，諸如儲能模量(楊氏模量)、損耗因子等力學特性參數。

大量的研究[7-9]已經發現硬涂層材料具有應變依賴性。所謂的應變依賴性實質上是一種對強迫振動響應幅度的依賴性，用于表征結構響應幅度的可以是振動位移、振動速度、振動加速度，當然也包括應變響應幅度，且目前已經習慣于用應變響應幅度來表征。在應變依賴性的影響下，硬涂層的儲能模量、損耗因子會隨著復合結構的應變響應幅度發生改變。硬涂層材料的應變依賴特性，也會使涂敷硬涂層的復合結構表現出變剛度、變阻尼的非線性振動特性。此外，硬涂層材料還具有受涂敷工藝影響明顯的特點，即同一種硬涂層材料，在不同制備工藝下，會表現出不同的力學特性參數。例如，PATSIAS等[10]分別測試了由等離子噴涂(APS)和電子束物理氣相沉積(EBPVD) 制備的同一種涂層的力學特性參數，結果發現兩者有很大的不同。可見，硬涂層材料的上述特點致使辨識硬涂層材料力學特性參數具有很大的挑戰性和迫切性。

針對硬涂層材料力學特性參數辨識需求，目前學者已提出多種方法，總體上可分為三種，分別為壓痕法[11]、彎曲測試法[12]、振動測試法[7-9,13]等。由于儀器設備簡單、操作方便，基于振動測試的辨識方法得到了廣泛的應用。在振動測試法中，應用較為廣泛的是基于Oberst beam理論的辨識技術，美國材料協會(American Society of Testing Materials，ASTM)[13]已將此項技術作為辨識涂層材料參數的一項基本技術。PATSIAS等[7]采用了Oberst beam 法進行了辨識硬涂層材料力學特性參數的實踐，通過測試懸臂梁試件的涂層前后的振動特性參數，獲得了硬涂層具有幅度依賴性的儲能模量和損耗因子。另一種基于振動法的測試技術其辨識原理同樣來自于梁理論，TORVIK[9]分別推導了涂層前后懸臂梁的儲能和耗能規律，并將具有應變依賴性的涂層參數用多項式表達，進而實現了考慮應變依賴性的硬涂層力學特性參數的辨識。

上述針對硬涂層材料參數的辨識主要針對涂層梁結構，為了獲得硬涂層材料參數，需要測試不同激勵幅度下涂層前后梁的振動特性參數，實驗工作量大且引入測試誤差的環節增多。由于處于共振狀態結構的自由振動衰減響應包含了即時響應、即時共振頻率、阻尼等大量信息。因而本文面向懸臂板結構，提出一種僅需測得涂層前后懸臂板的共振時域自由振動衰減響應，來辨識硬涂層材料力學特性參數的方法。首先確定了由自由振動衰減響應辨識硬涂層儲能模量及損耗因子的原理；進一步給出了獲得硬涂層材料參數所需的關鍵參數(例如響應包絡線、即時共振頻率、阻尼等)的辨識方法；再則描述了硬涂層板有限元建模以及共振頻率、模態應變能和參考應變的求解方法；最后以涂敷NiCoCrAlY+YSZ硬涂層的懸臂薄板為例進行了實例研究，獲得了該混合涂層的儲能模量及損耗因子，并簡要證明了所辨識的硬涂層材料參數的合理性。

1 辨識原理

具有應變依賴性的硬涂層材料參數可定義為

(1)

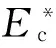
如果將硬涂層涂敷在已知材料參數的金屬基體上，當切斷處于共振狀態復合結構的激勵源時，可測試結構件上某點的自由振動衰減響應。該自由振動衰減響應中含有大量的信息，具體包括：①從自由振動衰減響應中可獲得包絡線，描述的是不同的位移響應幅度；②從自由振動衰減響應中可獲得隨時間變化的結構的即時共振頻率(或者稱之為時變共振頻率)；③從自由振動衰減響應中可獲得復合結構的阻尼，而且是一個時變的阻尼。這些信息通過恰當的處理則可以描述硬涂層材料的應變依賴性。以下說明硬涂層儲能模量及損耗因子的辨識原理。

1.1 硬涂層儲能模量的辨識原理

在薄板由共振狀態開始的自由振動衰減過程中，隨著響應幅度的減少，硬涂層的儲能模量會發生改變。進一步，硬涂層材料儲能模量的改變也會使整個復合板共振頻率發生變化。如果可以通過分析模型來捕捉該頻率的變化，并將分析結果與實測值進行比對，則可反推出隨應變變化的儲能模量值。相應的，面向薄板自由振動衰減響應的硬涂層儲能模量的辨識流程可用圖1來描述。

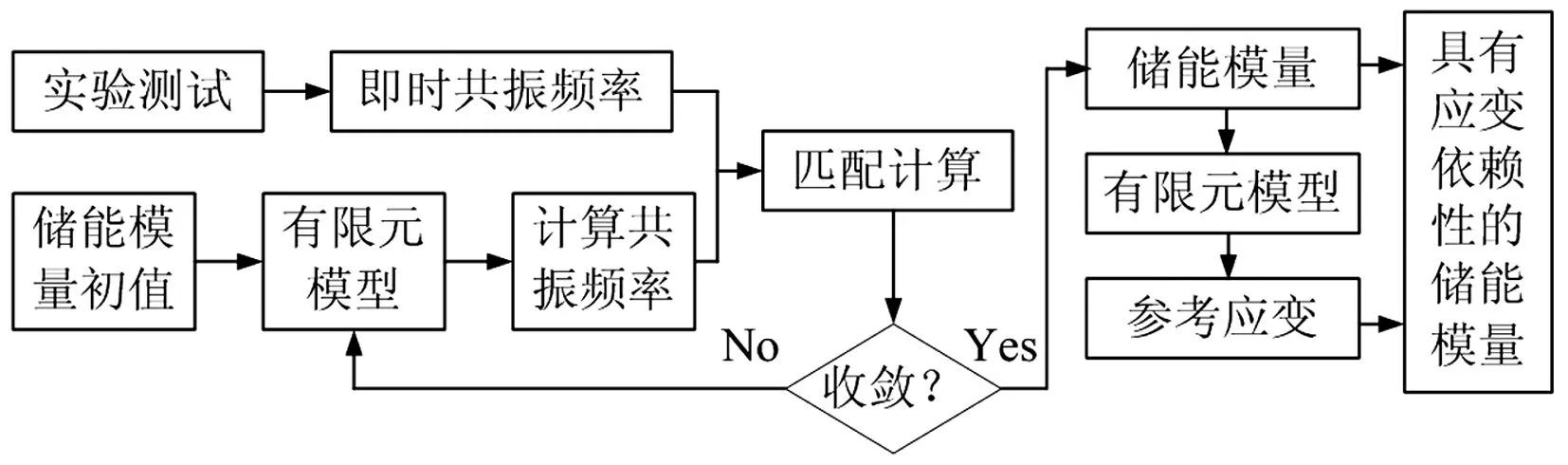
圖1 硬涂層儲能模量的辨識流程Fig.1 The procedure of identifying storage modulus of hard coating

圖1所示的是基于反推法辨識硬涂層儲能模量的流程。其基本思想是不斷地修正儲能模量值以使計算獲得的共振頻率與實測的即時共振頻率相一致，進而反推出硬涂層材料的儲能模量。由自由振動衰減數據獲得的即時共振頻率是一系列的離散點值，可選擇其中一部分將用于辨識硬涂層的儲能模量，關于即時共振頻率的辨識詳見第2部分。這里用有限元法作為工具計算硬涂層復合結構的共振頻率及用于表征應變依賴性的參考應變，詳見第3部分。

基于反推法辨識的核心是匹配計算，需要涉及模型修正技術[14]使理論分析的結果快速收斂于實驗值，進而反推出所辨識的硬涂層材料參數。基于模型修正技術的匹配計算原理如下：

設硬涂層的儲能模量EcR為模型修正技術中的設計變量。硬涂層復合板的第n階特征值λn對該設計變量的靈敏度SE,n，可表示為

(2)

式中，靈敏度采用差分法獲得，其設計變量變化量即步長ΔEcR設為10-4×EcR。φn為復合板的第n階模態振型，K和M分別為復合板的剛度及質量矩陣。

而特征值與共振頻率的關系，可表示為

λn=(2πfn)2

(3)

式中：fn為復合板的第n階即時共振頻率，單位為Hz。

模型修正技術的目標函數可按如下最小二乘原理來定義，即

Δλn=SE,nΔEcR

(4)

式中:Δλn為第n階特征值變化量，ΔEcR為儲能模量的變化量。在保證即時共振頻率得到修正的同時，要求設計變量的變化量盡可能的小，則最終的目標函數可描述為

(5)

相應的迭代公式為

(6)

式中:WE為儲能模量的修正加權系數。WE取0～0.3，設計變量不靈敏時需取高值，同時高的WE也意味著迭代次數需增加。由于振動衰減僅針對某一階次，可設置較高的精度。后續實例設收斂條件為修正后的計算共振頻率與相應的實驗值偏差在0.001%，經過若干次迭代，則可獲得對應于某一應變響應幅度下的儲能模量。

1.2 硬涂層的損耗因子辨識原理

硬涂層的損耗因子同樣具有應變依賴性，即在薄板由共振狀態開始的自由振動衰減過程中，硬涂層的損耗因子也會隨著響應幅度的減少而發生改變。基于自由振動衰減響應辨識硬涂層損耗因子的流程可用圖2來描述。

圖2 硬涂層損耗因子的辨識流程Fig.2 The procedure of identifying loss factor of hard coating

同樣，關于由自由振動衰減響應辨識涂層前后薄板損耗因子的方法參見第2部分，而關于基于有限元模型求解應變能和參考應變詳見第3部分。

在圖2所示的流程中，硬涂層損耗因子辨識計算公式是基于對涂層復合結構的儲能及耗能分析獲得的[15]，具體為

(7)

式中：η為涂層后薄板的損耗因子，ηs為涂層前板的損耗因子，RSE為硬涂層與基體的應變能比。可見，將不同響應幅度下涂層前/后損耗因子和對應的模態應變能比代入式(7)，進一步獲取對應的參考應變，則可求得具有應變依賴性的硬涂層損耗因子。

2 基于自由振動衰減響應的時變參數辨識

為了獲取硬涂層的力學特性參數，需要由硬涂層復合結構的自由振動衰減響應中獲取包絡線、即時共振頻率、阻尼等。以下詳細說明上述參數的提取方法。通常，結構的時域自由振動衰減響應中包含有大量的噪音，在上述參數辨識之前，還需進行降噪處理。這里采用十階巴特沃斯(Butterworth)帶通濾波器對時域振動衰減響應進行降噪處理。

2.1 提取包絡線

獲得的包絡線是后續阻尼辨識以及參考應變計算的重要依據。由于硬涂層復合板的自由振動衰減響應是一個非線性時變信號，這里采用分段處理。將原始信號分成若干時間段Δt，每段可近似為線性信號，并采用希爾伯特(Hilbert)變換來提取每個時間段對應的自由振動衰減響應的包絡線。

設對應于每個時間段，降噪后的衰減信號可表示為

(8)

式中：A為初始位移，ζn和ωn分別為第n階即時模態阻尼比和即時共振圓頻率。

對信號進行希爾伯特變換處理，有

(9)

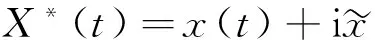
(10)

2.2 即時共振頻率辨識

由希爾伯特變換所獲得的分析信號，可得到自由衰減信號的即時相位φ(t)，求解式為

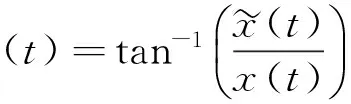
(11)

進一步，由即時相位就可獲得硬涂層板的即時共振頻率ωn(t)，求解式為

(12)

需要說明的是上述即時共振頻率的求解同樣也是針對各時間段內的數據而進行的。最終經差分處理，則可獲得每個時間段Δt內近似為常值的共振頻率。

2.3 阻尼辨識

由圖2所示的辨識流程可知，阻尼辨識需同時針對同一階次的涂層前后薄板共振狀態的自由振動衰減數據，但兩者在辨識方法上是一致的。這里利用獲得的包絡線數據來辨識薄板系統的阻尼(用模態損耗因子來描述)。考慮到損耗因子的時變性，對應于每個時間段的數據采用如下公式進行辨識

(13)

(14)式中：X1，X2為包絡線上時間間隔為Δt兩點處的響應值。這樣處理后對應每個時間段的損耗因子也為常值。

這種針對時域自由振動衰減響應分段處理的參數辨識方法，即可以很好地描述硬涂層材料的應變依賴特性，又可以最大限度的減少噪音對辨識結果的干擾。通過以上處理就獲得了各時間段Δt對應的包絡線、即時共振頻率、阻尼等參數。每個時間段Δt對應的數據可作為具有應依賴性的硬涂層材料參數辨識的一個數據點。

3 薄板固有特性及參考應變計算

這里，選用ANSYS軟件，按照有限元法對涂層薄板結構進行動力學建模及分析。參照圖1和圖2所示的流程可知，有限元計算的內容包括共振頻率計算、模態應變能計算和參考應變計算。計算的結果用于辨識具有應變依賴性的硬涂層材料參數，計算的次數與所選用的時間段數量相等。另外，上述計算的順序也不能改變，因為后一個計算要基于前一個計算的結果。以下簡要說明相關計算方法。

共振頻率的計算主要用于辨識硬涂層的儲能模量，為了考慮阻尼的影響，做了如下修正

(15)

式中：fupdated和fFEM分別為修正的共振頻率和有限元模態計算獲得的共振頻率，ζn通常為模態損耗因子的1/2。參照后續的實驗結果可知涂敷硬涂層后復合板的模態損耗因子小于0.01，因而實際上fupdated和fFEM的結果相差不大。

按照設定的優化模型，需要進行一系列的迭代計算使計算獲得的共振頻率與試驗中每個時間段確定的即時共振頻率差值最小，從而反推出儲能模量值。

參照式(7)可知，模態應變能的計算主要用于獲得硬涂層及基體的應變能比RSE，相應的計算式為

(16)

式中：Kc，Ks分別為涂層與基體的剛度矩陣。在ANSYS中，可以直接在后處理中提取上述應變能。同樣針對每一個儲能模量值，都要進行一次模態應變能計算，相關結果用于硬涂層損耗因子的辨識。

在復合結構的某一響應幅度下，通常選擇硬涂層和基體結合面處的最大應變來作為參考應變描述硬涂層能材料的應變依賴特性。由于本文的研究對象為薄板結構，單獨選擇任意方向的應變作為參考應變是不科學的，需要選擇等效應變來作為描述硬涂層應變依賴性的參考應變。薄板結構等效參考應變εe可按照應變能密度相等的原則來定義，具體為

σeεe=σxεx+σyεy+τxyγxy

(17)

式中:σx,σy和εx,εy分別為x及y方向的正應力及正應變，τxy和γxy分別為xy平面內的剪應力和剪應變，σe為等效應力。參考應變的計算仍舊與各時間段的辨識或分析數據相對應，具體方法可描述為：將辨識獲得的儲能模量及復合結構損耗因子代入有限元模型；施加激勵并調整激勵幅度值直到分析與實測的自由振動衰減響應幅度近似一致為止；參見模態振型，獲得最大應變的位置；提取該最大應變處的等效應變即為該自由振動衰減響應幅度對應的參考應變。

4 研究實例

這里以涂敷NiCoCrAlY+YSZ硬涂層的懸臂薄板為例來演示本文所研發的算法。

4.1 測試試驗件及實驗系統

涂敷NiCoCrAlY+YSZ硬涂層前后的鈦板見圖3。該薄板的長、寬分別為153.1 mm，109.6 mm，鈦板基體的厚度為1.44 m。在薄板的一側涂敷硬涂層，涂層厚度為0.3 mm。薄板夾持區長度為20 mm。鈦板的材料參數是已知的，具體為：儲能模量110.32 GPa，密度4 420 kg/m3，損耗因子0.000 7。硬涂層的密度可由實測獲得具體為5 600 kg/m3，硬涂層及鈦板的泊松比均取0.3，硬涂層的其他材料參數，包括儲能模量和損耗因子則需要辨識獲得。

圖3 鈦板實驗件Fig.3 Titanium test pieces

這里采用振動臺基礎激勵，在獲得涂層前后薄板共振點的前提下，用共振頻率激勵來獲得涂層前后薄板的自由振動衰減響應。實驗現場見圖4，所涉及的儀器設備見表1。用激光測振儀拾振，參見圖4中的坐標，拾振點為x=29 mm，y=41 mm。表1中的PCB模態力錘主要用于測試涂層板前6階共振頻率，相應的結果用于后續校驗所辨識的硬涂層材料參數的合理性。

圖4 硬涂層板基礎激勵測試Fig.4 The test of hard-coating plate under base excitation

序號名稱1LMS16通道便攜式數據采集前端控制器2PolytecPDV-100激光多普勒測振儀3LMS.Testlab筆記本工作站4KINGDESIGNEM-1000F振動臺5PCB8206-00154627模態力錘

4.2 硬涂層力學特性參數辨識

這里以涂層前后懸臂板的第6階為對象，由第6階共振自由振動衰減響應辨識具有應變依賴性硬涂層的力學特性辨識。在4 g激勵幅度下，首先由掃頻三維瀑布圖獲得涂層前后薄板的共振頻率分別為，1 297 Hz(涂層前)，1 259.13 Hz(涂層后)。進一步分別用共振頻率激勵涂層前后的薄板，待響應穩定后停止激勵，進而就可以獲得涂層前后薄板的時域共振衰減響應。

以下僅以涂層后的薄板為例，說明數據處理過程。選用十階巴特沃斯帶通濾波器，頻率范圍設置為1 259.5～1 261.5 Hz對自由振動衰減信號進行降噪處理，并用希爾伯特變換提取包絡線，降噪信號及包絡線見圖5。為了有效辨識，這里選擇0～0.1 s的數據，每間隔0.05 s非連續地取出10個時間段用來進行即時共振頻率及損耗因子的辨識。需要說明的是在本實例中，包絡線辨識所選用的時間段數量遠大于上述值，覆蓋了整個自由振動衰減的時間范圍(見圖5)。接下來，針對每個時間段的數據，用差分法求得的即時頻率，按式(13)和式(14)求得損耗因子。最終，對應各時間段，經上述操作獲得了用于辨識硬涂層材料力學特性參數所需的所有參數。相關結果均列在表2中，具體包括涂層板的即時共振頻率、位移響應、損耗因子以及未涂層板的損耗因子。此外還需說明的是由于實測的是速度響應v，這里利用v/ωn將其轉化為位移響應。

創建硬涂層板的有限元模型，見圖6。在該有限元模型中，基體及涂層板均采用SHELL281單元，在整個模型中共有800個單元， 2 562個節點。基于這個有限元模型進行匹配迭代計算，就可以獲得對應上述10個時間段的硬涂層儲能模量。接著，將獲得的硬涂層儲能模量重新輸入有限元模型中，按式(16)獲得硬涂層及基體的模態應變能比。進一步分別將上述應變能比以及表2中涂層前后損耗因子代入式(7)，則可獲得對應上述各時間段的硬涂層的損耗因子。最后，分別將獲得的儲能模量及復合板損耗因子輸入有限元模型，參照各時間段的位移響應，按第3部分所描述的方法就可以確定對應各位移響應的參考應變。上述所有辨識結果均列在表3中。由表3可知，這里獲得的硬涂層材料參數的應變依賴性不強，這是由于激勵能量(或者激勵幅度)較小所造成的。

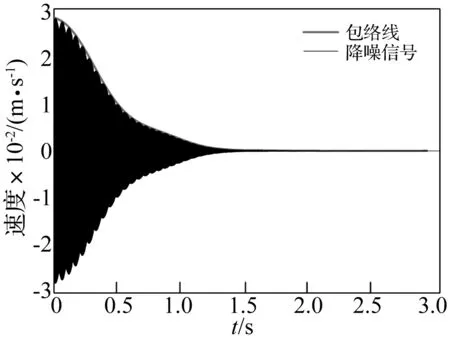
圖5 涂層板第6階共振自由振動衰減信號及包絡線Fig.5 Free decay signal and envelop of coated plate for the 6th order resonance

參照表3，以參考應變為橫軸，分別以硬涂層儲能模量及損耗因子為縱軸，則可以確定具有應變依賴性的力學特性參數，相關結果見圖7。由圖7可知，辨識獲得的硬涂層儲能模量隨參考應變的增大而減小，而損耗因子則隨參考應變先增大再減小，上述變化規律同其他文獻結果基本一致。只是本文是針對硬涂層懸臂板結構，而其他文獻均是針對梁型試件。考慮到硬涂層力學特性參數隨工藝變化明顯這一特點，如果需針對硬涂層板形結構進行建模，本文所辨識的結果可以被直接應用。

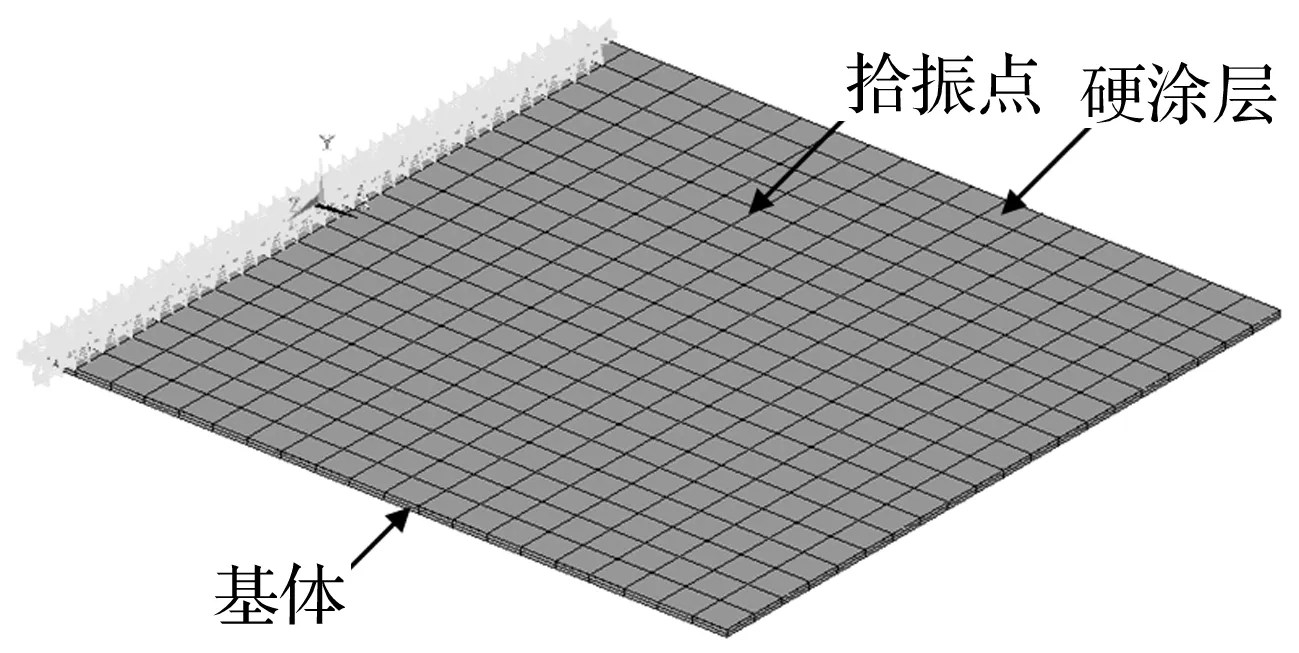
圖6 硬涂層懸臂板有限元模型Fig.6 FE model of hard-coating cantilever plate

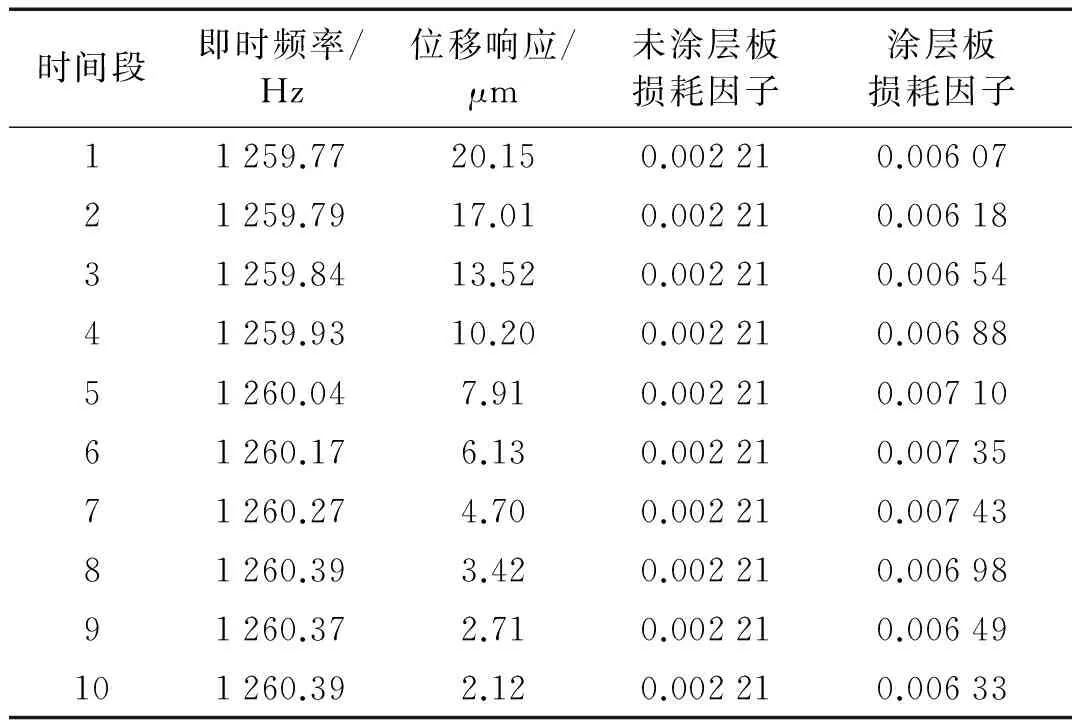
時間段即時頻率/Hz位移響應/μm未涂層板損耗因子涂層板損耗因子11259.7720.150.002210.0060721259.7917.010.002210.0061831259.8413.520.002210.0065441259.9310.200.002210.0068851260.047.910.002210.0071061260.176.130.002210.0073571260.274.700.002210.0074381260.393.420.002210.0069891260.372.710.002210.00649101260.392.120.002210.00633

表3 硬涂層力學特性參數辨識結果Tab.3 Identification results of mechanical parameters of hard coating

圖7 硬涂層力學特性參數的應變依賴性表征Fig.7 Characterization of hard-coating mechanical parameters with strain dependent characteristics

4.3 辨識的硬涂層參數合理性驗證

為了證明所辨識的硬涂層參數的合理性，以下將辨識的硬涂層材料參數代入到所創建的硬涂層板有限元模型中，計算前6階共振頻率。同時利用錘擊法測試涂層板的前6階共振頻率，在錘擊測試中拾振點與圖4一致，敲擊位置在薄板的右側邊緣。計算結果、測試的結果以及兩者的比較均列在表4中。需要說明的是考慮到所辨識的硬涂層材料參數應變依賴性不強，因而這里僅取時間段1對應的材料數據，進行有限元計算，因而這是一種粗略的計算。由表4可知，用針對第6階共振自由振動衰減響應辨識得到硬涂層材料參數計算獲得的硬涂層板前6階共振頻率與錘擊法實測的結果基本一致，因而可以說明這里所辨識的硬涂層材料參數具有合理性。

5 結 論

獲得硬涂層材料的儲能模量和損耗因子等力學特性參數，對于硬涂層復合結構建模及阻尼減振優化設計都有重要的意義。本文研發了從涂層前后薄板結構共振狀態下的自由振動衰減響應來辨識上述硬涂層材料力學特性參數的方法，得出以下結論。

(1)研究的實踐表明，基于涂層前后薄板共振狀態下的自由振動衰減響應，采用反推法并利用匹配計算可獲得硬涂層的儲能模量，利用涂層前后結構件的儲能及耗能規律公式，可確定硬涂層的損耗因子。

(2)相對于現有的、需要多個激勵幅度測試的硬涂層材料力學特性參數的辨識方法，本文所研發的方法實驗量較少。只需測得某一激勵幅度下涂層前后薄板同一階次的共振狀態自由振動衰減響應就可實現硬涂層參數的有效辨識。

(3)本文提出對時域自由振動衰減響應分段處理的參數辨識方法。這樣做的好處是一方面可以很好地描述硬涂層材料的應變依賴特性，另一方面可以最大限度的減少噪音對辨識結果的干擾。

(4)將獲得的硬涂層材料參數代入到有限元分析模型，通過對比試驗與有限元計算獲得的硬涂層板前6階共振頻率，發現兩者結果基本一致。此外，發現本文辨識獲得的硬涂層儲能模量及損耗因子隨參考應變幅度變化的規律同其他相關文獻結果也是基本一致。從而證明了本文所辨識的硬涂層材料參數的合理性。這里針對的是硬涂層懸臂板結構，而其他文獻均是針對梁形試件。考慮到硬涂層力學特性參數隨工藝變化明顯這一特點，如果需針對硬涂層板形結構進行建模，本文所辨識的結果可以被更加直接地應用。

[1] BLACKWELL C, PALAZOTTO A, GEORGE T J, et al. The evaluation of the damping characteristics of a hard coating on titanium[J]. Shock and Vibration, 2007,14(1): 37-51.

[2] IVANCIC F, PALAZOTTO A. Experimental considerations for determining the damping coefficients of hard coatings[J]. Journal of Aerospace Engineering,2005,18(1):8-17.

[3] 孫偉，齊飛 ，韓清凱. 基于自由振動衰減信號包絡線法辨識硬涂層復合結構的阻尼特性[J]. 振動與沖擊，2013,32(12)：50-54. SUN Wei, QI Fei, HAN Qingkai. Estimating system damping for a hard coating composite structure based on envelope of a free damped vibration signal[J]. Journal of Vibration and Shock, 2013,32(12)：50-54.

[4] TASSINI N, PATSIAS S, LAMBRINOU K. Ceramic coatings: a phenomenological modeling for damping behavior related to microstructural features[J]. Materials Science and Engineering: A, 2006, 442(1): 509-513.

[5] TORVIK P J. A slip damping model for plasma sprayed ceramics[J]. Journal of Applied Mechanics, 2009, 76(6): 061018.

[6] AL-RUB R K A, PALAZOTTO A N. Micromechanical theoretical and computational modeling of energy dissipation due to nonlinear vibration of hard ceramic coatings with microstructural recursive faults[J]. International Journal of Solids and Structures, 2010, 47(16): 2131-2142.

[7] PATSIAS S, SAXTON C, SHIPTON M. Hard damping coatings: an experimental procedure for extraction of damping characteristics and modulus of elasticity[J]. Materials Science and Engineering: A, 2004, 370(1): 412-416.

[8] TASSINI N, LAMBRINOU K, MIRCEA I, et al. Study of the amplitude-dependent mechanical behaviour of yttria-stabilised zirconia thermal barrier coatings[J]. Journal of the European Ceramic Society, 2007, 27(2): 1487-1491.

[9] TORVIK P J. Determination of mechanical properties of non-linear coatings from measurements with coated beams[J]. International Journal of Solids and Structures, 2009, 46(5): 1066-1077.

[10] PATSIAS S, TASSINI N, LAMBRINOU K. Ceramic coatings: effect of deposition method on damping and modulus of elasticity for yttria-stabilized zirconia[J]. Materials Science and Engineering: A, 2006, 442(1): 504-508.

[11] WEI P J, LIN J F. A new method developed to evaluate both the hardness and elastic modulus of a coating-substrate system [J]. Surface & Coatings Technology, 2005, 200(7): 2489-2496.

[12] KIM H J, KWEON Y G. Elastic modulus of plasma-sprayed coatings determined by indentation and bend tests [J]. Thin Solid Films,1999, 342(1/2):201-206.

[13] ASTM International. ASTME756-04 standard test method for measuring vibration-damping properties of materials[S]. 2005.

[14] MOTTERSHEAD J E, LINK M, FRISWELL M I. The sensitivity method in finite element model updating: a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2275-2296.

[15] 孫偉，賈師，劉營. 硬涂層懸臂梁減振機理分析模型的建立[J]. 東北大學學報(自然科學版)，2015, 36(5): 695-698. SUN Wei, JIA Shi, LIU Ying. Establishment of model of damping mechanism for the hard-coating cantilever beam[J]. Journal of Northeastern University(Natural Science), 2015, 36(5): 695-698.

Identification of the mechanical parameters of hard coating based on free vibration decay response

SUN Wei, WANG Zhuo

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Obtaining the mechanical parameters of hard coating is the premise of modeling and damping design of a hard-coating composite structure. Most studies about identifying the mechanical parameters of hard coating are based on beam specimen and a complex test procedure. Here, a cantilever thin plate structure was considered. A new identification method was presented, which only needed to test the free vibration decay responses from resonance status for the uncoated and coated plate. Firstly, based on the free vibration decay responses, the principles of identifying storage modulus and loss factor of hard coating were proposed. Then, to effectively obtain the mechanical parameters of hard coating, the method of identifying some key parameters (such as envelop of response, instant resonance frequency and damping) was given. Next, the FEM modeling of hard-coating plate and solution of resonance frequency, modal strain energy and reference strain were described. Finally, the cantilever thin plate coated NiCoCrAlY+YSZ hard coating was chosen to demonstrate the proposed method. The storage and loss factor of this mixing coating were identified. Furthermore, the obtained material parameters were inputted into the created FEM model and the rationality of identified parameters was proved by comparing the first 6 orders resonance frequency obtained by measurement and FEM calculation respectively. The identification results show the change rules of storage modulus and loss factor of hard coating with the strain amplitude are consistent with the results listed in other similar references. However, the results herein can more directly serve for the dynamic modeling of hard-coating plate-shape composite structures.

free vibration decay response; hard coating; mechanical parameters; identification of parameters

國家自然科學基金資助項目(51375079)

2015-07-02 修改稿收到日期：2015-11-16

孫偉 男，博士，副教授，1975年生

TB535

A

10.13465/j.cnki.jvs.2016.24.024