例談充分必要條件法解決數學問題的途徑

江蘇省啟東市呂四中學 周 華

例談充分必要條件法解決數學問題的途徑

江蘇省啟東市呂四中學 周 華

偵探小說愛好者熟知千篇一律的情節，把懷疑的范圍逐步縮小，最后偵探發現了罪犯。事實上，解數學題也存在著類似的情況，我們在解數學題時經常用到"充要條件"(即等價轉化)，但卻很少注重“充分條件”和“必要條件”的應用，本文旨在通過幾例說明“必要條件”在解題中的應用，先求出使得命題成立的“必要條件”，再由題設進一步求出使得命題成立的“充要條件”，從而解決問題。

必要條件；充要條件；定義域；充分條件；等價轉化

我們在平常的教學中可以看到，大部分學生對充分條件和必要條件的理解普遍感到十分困難，抓不住它的本質。雖然江蘇省高考數學考試說明中對這部分內容的要求不是太高，但它作為一種數學的解題思想，對培養學生理解問題和解決問題的能力是有很大用處的。

定義2：理解“充分”，“必要”詞語的含義并定性地判斷關系。“充分”相當于“有我便已足夠，無需其他”；“必要”相當于“沒它不行，但唯有它也未必行”。

眾所周知，等價轉化思想是一種重要的數學思想，在解題中的作用往往體現在化復雜為簡單，化陌生為熟悉，并且通過等價轉化得到的結論是不需要檢驗的。

但在數學解題中，有很多情形不易、不宜，甚至是不可能進行等價轉化，這時只有“退而求其次”，可以考慮用非等價轉化的方法來解題，常見的方法有“先必要后充分”和“先充分再必要”，本文主要談談先找出使結論成立的必要條件，然后再驗證其充分性。

一、運用充分必要條件法解決數列與不等式的綜合問題

數列是高中數學的一個重要的內容，也是歷年高考、競賽的常見題型，近幾年江蘇高考題很喜歡把數列定義成為壓軸題，用來拉開分數，選拔人才。呈現遞推關系的綜合性試題，特別是與不等式的綜合是教學的難點，往往入手比較困難，不容易想到解題思路，有時還會出現運算量比較大的情況，所以在此類問題中巧妙運用充分必要條件的解題思想往往會給解題帶來方便。

這個不等式不能解，如果硬做，只能通過取值一個一個進行嘗試可以得到答案，但是需要花的時間太長，在考試時很難算到答案。

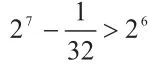
故可以判斷最大正整數n的值為12。

評注：此類問題，若按數列的基本思路循規蹈矩，即用等比數列的通項公式求出這個數列的通項公式代入不等式兩邊，然后解不等式。思路簡單、清晰，學生容易上手，但由于化簡得到的不等式較大，屬于不可解的不等式，代入檢驗的運算過程復雜，計算量大，需要學生有足夠的耐心和細心，一般學生很難解到最終的結果（具體解法略），但若能找到其必要條件把它配成可以解的不等式也許能很快找到結論。

二、運用充分必要條件解決含參數不等式恒成立問題

函數的基礎性強，特征性明顯，是高中數學教材中非常重要的部分，也是學生普遍覺得比較頭疼的問題。習題中對函數的考查也是必不可少的，而函數的單調性，有關函數的不等式恒成立問題是考查的一個重點和熱點內容。我們平常接觸的解決含有參數不等式恒成立的問題大概分成如下幾種：1.分離參數轉化為最值問題；2.直接轉化為最值問題；3.數形結合法。以上三種解法是幾種常用的基本方法，但是有些題目因為分離參數之后的函數表達式太大，導致到后面最值求不出來，從而得不到最終的結論。但如果能找到不等式成立的必要條件探索出參數的值，然后驗證其充分性也許會事半功倍。

（1）求函數f（x）的單調區間。

（2）若a=1，k為整數，且當x＞0時，，求k的最大值。

當a≤0，函數f（x）的增區間為（-∞，+∞）。

當a＞0函數f（x）的減區間為（-∞，lna），增區間為（lna，+∞）。

（2）當a=1，。 得到，代入不等式

這個時候直接求函數的最小值比較困難，轉而先找不等式恒成立的必要條件：

不等式對于x=1恒成立

然后驗證當k=2，在x＞0恒成立。

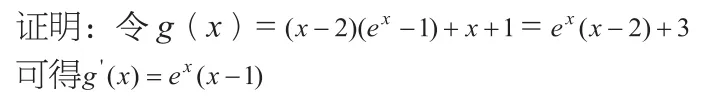
利用導數，可得函數g（x）在（0，1）為增函數，在（1，+∞）為減函數。

所以k=2,在x＞0恒成立。所以k的最大值為2。

評注：此類問題，用導數求解一類參數取值范圍或最值的問題在高考中很常見，而本題用常規的等價轉化即分離常數再求相應函數的最值難以求解，而解答方法——“先必要后充分”是一種容易掌握的好方法。函數導數的大題往往放在最后兩個題中，如果能夠掌握這種方法，就可以在高考中取得明顯的優勢。

化歸與轉化思想是數學中重要的思想方法之一，也是高考重點考查的方法之一。而大多數考題或者是大家的解題習慣多是實施等價轉化，即尋找題目求解的充要條件，很少涉及不等價轉化。以上幾道例題都有一定難度，而善于利用尋找必要條件，可以達到化繁為簡，化難為易，避免了分類討論，實現大題小做。因此，利用必要條件解題，可以縮小參數范圍，開闊解題思路，優化解題過程，提高學生的數學思維能力。