虛數到底有多能？再奇妙也不是萬能

河南省鄭州一中西校區高三（4）班 劉燁錕

虛數到底有多能？再奇妙也不是萬能

河南省鄭州一中西校區高三（4）班 劉燁錕

本文通過從虛數和復數的概念入手，嘗試尋找一個數“與 0相乘等于1”，但是通過對概念進行分析和數據進行運算不難發現，有時候為了實現一些不可能的運算而進行的假設，確實是違背數學常理的。

虛數；復數；0；1

數學是一門神奇的科學，小時候我們經常會想：為什么0乘以任何數都等于0呢？隨著年齡的增長，高中所學的數學知識和內容越來越多，在講到虛數和復數時，更加感受到數學的奧妙之處！在虛數的世界中似乎無所不能，虛數真的有這么強大嗎？本文通過從虛數和復數的概念入手，嘗試尋找一個數“與 0相乘等于1”，但是通過對概念進行分析和數據進行運算不難發現，有時候為了實現一些不可能的運算而進行的假設，確實是違背數學常理的。

一、虛數

“虛數”這個名詞是17世紀著名數學家、哲學家笛卡爾創制，因為當時的觀念認為這是真實不存在的數字。后來發現虛數可對應平面上的縱軸，與對應平面上橫軸的實數同樣真實。

人們發現即使使用全部的有理數和無理數，也不能解決代數方程的求解問題。像x2+1=0這樣最簡單的二次方程，在實數范圍內沒有解。到了16世紀，意大利數學家卡爾達諾在其著作《大術》（《數學大典》）中，把記為1545R15-15m這是最早的虛數記號。但他認為這僅僅是個形式表示而已。1637年法國數學家笛卡爾，在其《幾何學》中第一次給出“虛數”的名稱，并和“實數”相對應。

直到19世紀初，高斯系統地使用了i這個符號，并主張用數偶（a、b）來表示a+bi，稱為復數，虛數才逐步得以通行。由于虛數闖進數的領域時，人們對它的實際用處一無所知，在實際生活中似乎沒有用復數來表達的量，因此在很長一段時間里，人們對它產生過種種懷疑和誤解。

繼歐拉之后，挪威測量學家維塞爾提出把復數（a+bi）用平面上的點來表示。后來高斯又提出了復平面的概念，終于使復數有了立足之地，也為復數的應用開辟了道路。現在，復數一般用來表示向量（有方向的量），這在水利學、地圖學、航空學中的應用十分廣泛，虛數越來越顯示出其豐富的內容。

二、復數

要進行虛數的運算，首先要知道復數的定義。既然i表示旋轉量，我們就可以用i，表示任何實數的旋轉狀態。

將實數軸看作橫軸，虛數軸看作縱軸，就構成了一個二維平面。旋轉到某一個角度的任何正實數，必然唯一對應這個平面中的某個點。

只要確定橫坐標和縱坐標，比如(1 ,i)，就可以確定某個實數的旋轉量（45度）。

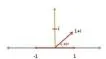
數學家用一種特殊的表示方法，表示這個二維坐標：用 + 號把橫坐標和縱坐標連接起來。比如，把 (1,i) 表示成1 +i。這種表示方法就叫作復數（complex number），其中 1 稱為實數部，i稱為虛數部。

三、與 0 相乘等于1，是奇跡？要實現還是違背了常理

這個思路緣于一次數學課上，老師在講虛數的時候，老師給我們出了一個問題：列個式子算算最后算的結果是對-1開平方。大家都無從下手的時候，老師說：“咱們定義一個i，它的平方等于-1，看，這個式子就有結果了，答案是i。”全班同學都恍然大悟！

此時我想：為什么不能定義一個數，和0相乘等于1呢？這樣其他數除以0就有結果了。老師說：0不能做除數！但是我想：負數也不能開平方啊。老師這個時候強調到：虛數i。聽完老師的話，我又通過一系列的學習，認識到：虛數是有實用性的，所以才有了i，那么會不會存在這個l，與 0 的乘積等于1呢?

將自己的思路梳理清楚之后，我總結出來要解答這個問題需要先解決兩個問題：

1.把－1的平方根加進實數是否可行？

2.可不可以把1/0加進實數？

首先我們要明確復數域嚴格定義，即：復數域，由復數和數域兩個詞合成。復數是指形如“a+bi”一類的數，其中a，b都是實數，i=根號(-1)，稱虛數單位。數域是數的一種集合。滿足以下條件∶

①如果a，b是集合中的任意兩個數，那么a+b和a-b也在這個集合中；

②如果a，b是集合中的任意兩個數，那么a＊b和a/b(b≠0)也在這個集合中。

由此可見，復數相比實數并不單純是加了個i這么簡單，還需說明加了這個i之后和原有的代數系統是相容的。因此我們可以得出結論：把－1的平方根加進實數是一個可行的操作，且不能把1/0加進實數，因為這樣做會破壞實數的代數結構。0最基本的意義是加法單位元，1最基本的意義是乘法單位元，所以我們討論的結構一定是一個集合S配上一個加法和一個乘法，首先要要求加法和乘法之間滿足分配率，如果要實現一個數和0相乘為1，就會破壞實數的性質，它會強迫0=1，這樣做會導致所有的元素都等于0，這樣得到的數集就只含有一個元素，實數的運算規則也就被破壞了。

在一些最基本的假設（乘法加法和它們之間的相容性），加法有逆元（無論左逆還是右逆），更進一步，假如加法單位元的乘法左逆有加法右逆（或 乘法右逆有加法左逆），則這個奇奇怪怪的代數結構只能是單點集合和平凡的加法乘法，奇妙的運算是奇跡還是違背常理，深入剖析基礎概念進行運算就能見分曉。

[1]M.克萊因.數學：確定性的喪失[M].李宏魁，譯.長沙：湖南科學技術出版社，1997.

[2]M.克萊因.古今數學思想（第4冊）[M].北京大學數學系數學史翻譯組，譯.上海：上海科技出版社，1981.