大音希聲 大象無形*——基于2016年浙江省數(shù)學(xué)高考理科第15題

●李學(xué)軍 曲文瑞

(平湖中學(xué) 浙江平湖 314200)

?

大音希聲 大象無形*
——基于2016年浙江省數(shù)學(xué)高考理科第15題

●李學(xué)軍 曲文瑞

(平湖中學(xué) 浙江平湖 314200)

作為數(shù)學(xué)教師，要研究解題，要研究學(xué)生的解題，引導(dǎo)學(xué)生用數(shù)學(xué)的思維思考和解決問題，去體會和體驗在解題過程中的糾結(jié)和成功之后的快樂，實現(xiàn)真正意義的數(shù)學(xué)學(xué)習(xí).文章基于2016年浙江省數(shù)學(xué)高考理科第15題(平面向量試題)進(jìn)行分析、歸納和提升，從而感受高考試題的樸素美.

高考題；考題解法；教學(xué)啟示

2016年的高考早已經(jīng)落下帷幕，但關(guān)于高考的話題還是各界人士談?wù)摰臒狳c和焦點，無論在學(xué)校的教師當(dāng)中，還是在各個數(shù)學(xué)交流群里，對于高考試題解法的探究和試題背景的研討比比皆是.筆者認(rèn)為，學(xué)生至少要有一杯水，教師需要如何做呢？是把教師的至少一桶水給學(xué)生舀一杯，還是把這一桶水放在學(xué)生面前讓學(xué)生根據(jù)需要來自己舀呢？還是給學(xué)生提供水源的地圖讓學(xué)生自己尋找呢？數(shù)學(xué)家克萊因說過：“教師掌握的知識要比他所教的知識多得多，才能引導(dǎo)學(xué)生繞過懸崖、渡過險灘.”學(xué)生平時在做數(shù)學(xué)題的時候，大多數(shù)是尋找曾經(jīng)做過的題目的感覺，對于呈現(xiàn)在他們面前的數(shù)學(xué)試題，不能很好思考試題的根本考點，考查的基本數(shù)學(xué)方法，當(dāng)在遇到陌生的數(shù)學(xué)試題時，有時候就有一種對思考方向暫時失憶的感覺.關(guān)于2016年浙江省數(shù)學(xué)高考理科卷第15題，筆者試著從一名普通考生的角色出發(fā)，對該題進(jìn)行解答、探索，并把筆者的尋題歷程及題后感悟呈現(xiàn)如下.

1 考題再現(xiàn)，返樸歸真

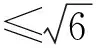
(2016年浙江省數(shù)學(xué)高考理科試題第15題)

本題作為填空題的壓軸題，具有非常好的選拔功能；題干表述簡潔明了，具有非常明顯的浙江風(fēng)格.本題考查了平面向量投影的概念，由于平面向量是代數(shù)和幾何的橋梁，因此本題可以通過代數(shù)和幾何2條途徑入手解答.正如章建躍先生曾說：要讓學(xué)生養(yǎng)成“回到概念去”思考和解決問題的習(xí)慣[1].在考試的過程中，學(xué)生更應(yīng)該從概念入手，從問題的本質(zhì)出發(fā)對問題進(jìn)行轉(zhuǎn)化和化歸，一定可以達(dá)到理想的效果.

2 解法探究，拋磚引玉

視角1 坐標(biāo)的視角

|a·e|+ |b·e|=

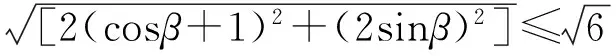
即

5+4cosβ≤6,

于是

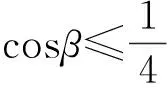
進(jìn)而

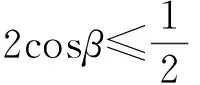
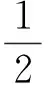
點評 利用坐標(biāo)法來解決平面向量問題，實際上就是把抽象的向量問題轉(zhuǎn)化為坐標(biāo)運算，這種解法對于學(xué)生來說，“痛處”在于如何恰當(dāng)?shù)亟⑵矫嬷苯亲鴺?biāo)系,以及接下來的問題轉(zhuǎn)化，然后再整理出關(guān)系式，通過建立直角坐標(biāo)系，引進(jìn)變元化歸為三角函數(shù)的問題.由于該考題是求最大值，通過分析2個向量的夾角應(yīng)該是銳角，因此對夾角的限制減少了很多的麻煩.由于要研究的是的最大值問題，因此，這種解法的巧妙之處是先進(jìn)行問題的轉(zhuǎn)化，然后在進(jìn)行數(shù)據(jù)處理，這種處理問題的方式更是一種思維上的提升.

視角2 代數(shù)的視角

分析 設(shè)=α,=β.因為

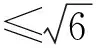
所以

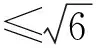
令sinα+2sinβ=t,2個式子平方得

cos2α+4|cosα||cosβ|+4cos2β+sin2α+

4sinαsinβ+4sin2β≤6+t2,

從而

4(|cosαcosβ|+sinαsinβ)≤t2+1.

對任意的實數(shù)α，β上式恒成立，因此4(|cosαcosβ|+sinαsinβ)≤(t2+1)min,于是

4(|cosαcosβ|+sinαsinβ)≤1,

進(jìn)而

|a·b|= 2(cosαcosβ+sinαsinβ)≤

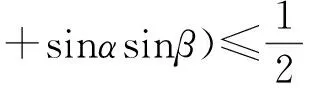
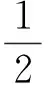
點評 根據(jù)題干中的條件，要想把向量數(shù)量積的絕對值表示出來，從定義的角度入手首先要引入向量的夾角，同時通過分析得出當(dāng)a·b取得最大值時，一定是銳角，接下來處理最值的本質(zhì)在哪里呢？想辦法“減元”.本題的“減元”通過聯(lián)想到形式相似，引進(jìn)等式，通過平方變形進(jìn)而很好地達(dá)到目的.對于給出同樣的代數(shù)式，觀察的角度不同，就會產(chǎn)生不一樣的想法，對于處理雙變元函數(shù)問題的化歸就是想辦法進(jìn)行減元，這個轉(zhuǎn)化非常關(guān)鍵.

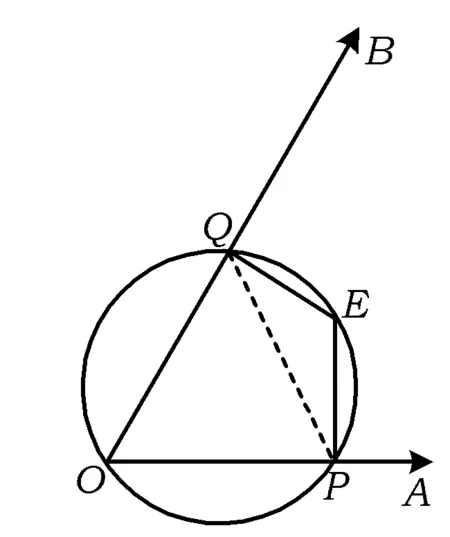
圖1

視角3 幾何的視角

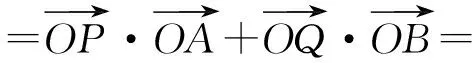
于是

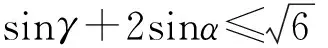
點評 從幾何的角度進(jìn)行思考，對于那些幾何背景素養(yǎng)較高的學(xué)生來說，結(jié)合平面向量的幾何背景入手，可以先從一些特殊圖形出發(fā)，然后進(jìn)行歸納分析，從而得到最值.對于2016年的考題來說，通過畫出一些圖形分析得到的是圓中的問題，從而從圓的角度出發(fā)分析，使得比較抽象的問題轉(zhuǎn)化為實實在在的平面幾何問題.學(xué)習(xí)數(shù)學(xué)不可忽略非常重要的數(shù)學(xué)思維，即歸納—猜想—論證.歸納至少要有3個數(shù)據(jù)，因此我們要想辦法找到這些數(shù)據(jù)，有這樣的思維方式，找的數(shù)據(jù)越多越容易歸納出結(jié)論，然后就比較容易進(jìn)行論證.這樣處理問題的方式能很好地避開繁瑣的計算,但在平時缺少訓(xùn)練.

視角4 構(gòu)造的視角

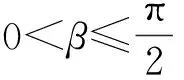
分析 根據(jù)三角不等式

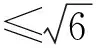
可知

政府投資項目工程造價結(jié)算審計質(zhì)量提升過程中，需要規(guī)范項目立項報批程序和審核流程。規(guī)范項目立項報批時，結(jié)算審計人員要遵循國家關(guān)于結(jié)算審計的相關(guān)規(guī)章制度，認(rèn)真檢查結(jié)算審計決策，明確資金、設(shè)備、人員等到位情況。同時，明確審計相關(guān)規(guī)章制度，將工程造價控制在合理范圍內(nèi)。在對審核流程進(jìn)行規(guī)范期間，需要認(rèn)真核對接到的結(jié)算審計任務(wù)，根據(jù)實際施工情況修正工程量，通過審核的方式明確工程量有無錯漏，無錯漏直接出版，有錯漏即返回到修正工程量重新審核。

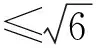
從而

a2+2a·b+b2≤6，

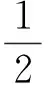
點評 除了上述通性通法，也可以通過構(gòu)造法進(jìn)行解決(可構(gòu)造三角不等式，三角不等式來源于幾何圖形).筆者認(rèn)為:該方法之所以隱蔽，比較難考慮到，主要還是陷入到平面向量的考點當(dāng)中，正所謂當(dāng)局者迷；還有一個原因是平時三角不等式的使用頻率不高，不夠熟練.

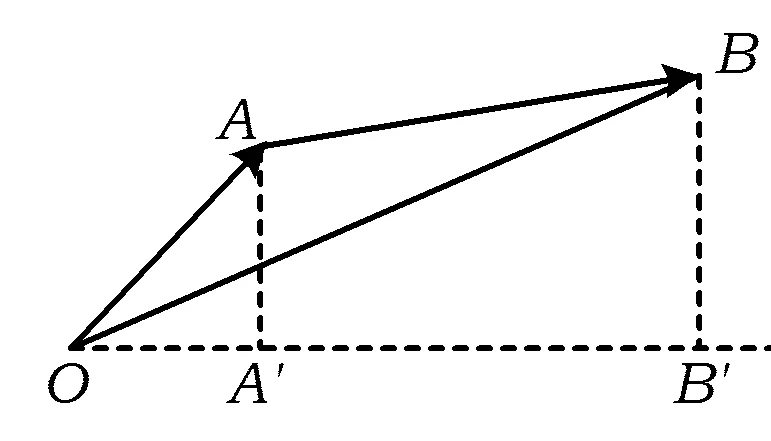
圖2

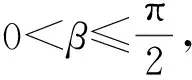
視角5 投影的視角

|a·e|+ |b·e|=

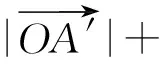
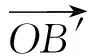
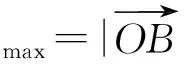
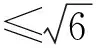
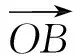
即

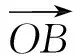
于是

a2+2a·b+b2≤6,

故

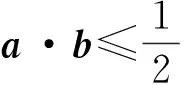
點評 本題給出的2個絕對值之和，也就是2條線段之和，是否可以讓2條線段之和看起來更直接呢？對向量進(jìn)行首尾順次聯(lián)結(jié)轉(zhuǎn)化，那么投影線段也就變成了一條線段，在這樣的構(gòu)造中，還有非常重要的知識理解，就是任意單位向量e，實際上給出的是直線的方向向量，要求的是向量a,b在直線l上的投影線段.

3 解后反思，引領(lǐng)教學(xué)

3.1 重視概念，關(guān)注本質(zhì)

在高考試卷中，對知識概念的考查，對問題本質(zhì)的考查可以說是比比皆是，應(yīng)該說是考查的重點.在數(shù)學(xué)中學(xué)生要能夠?qū)崿F(xiàn)文字語言、符號語言、圖形語言的交融，在審清題意的基礎(chǔ)上才能想明白、才能夠找到數(shù)學(xué)問題的本質(zhì)，把解決問題的思路較好地進(jìn)行內(nèi)化.學(xué)生說的更高層次是透過問題的本質(zhì)、背景、相似或相關(guān)的數(shù)學(xué)問題進(jìn)行輻射，逐步引導(dǎo)學(xué)生去悟，直到學(xué)生自發(fā)地悟，形成自己的解決問題的能力和解決問題方法.轉(zhuǎn)化是數(shù)學(xué)中非常重要的數(shù)學(xué)思想，轉(zhuǎn)化可以是表達(dá)方式的轉(zhuǎn)化，可以是形與形之間的轉(zhuǎn)化，可以是文字語言、符號語言、圖形語言之間的轉(zhuǎn)化，還可以是解題方法的轉(zhuǎn)化.

3.2 通法入手，巧法滲透

高考是選拔性考試，既要保證考生在考場上把尋常路走好，同時又要讓那些有創(chuàng)造性的考生能夠脫穎而出.因此在試題的設(shè)置上表現(xiàn)為“通性通法”重點考查，又會在試卷中適當(dāng)加入一些“技巧性元素”進(jìn)行錦上添花.因此，在平時的教學(xué)中，要求教師更加注重對知識“通性通法”的教學(xué).而事實上，技巧性解法的發(fā)現(xiàn)，也就是通性通法的提升和化歸[2].只要對問題解決的通性通法過關(guān)、熟練、高效，某些試題的技巧性解法自然就會應(yīng)運而生.3.3 夯實基礎(chǔ)，提升能力

在高考卷中，題目的難易程度都是有要求的，基礎(chǔ)題、中檔題、難題的設(shè)置是有一定比例的.對于教師而言，應(yīng)該重視基礎(chǔ)題的訓(xùn)練，規(guī)范解題，做到有理有據(jù)，對于計算及數(shù)據(jù)處理，注重準(zhǔn)確、速度.對于高考卷來說，考生在對難題的處理是多方面的：首先要保證時間，安排好難題的思考時間；其次是難題到基礎(chǔ)題的分解.如果考生的基本功過關(guān)，就基本具備了解決難題的素質(zhì).

3.4 著眼專題，優(yōu)化解題

對于數(shù)學(xué)學(xué)科來說也是有一定量的母題或者說是題根的，非常多的題目是可以找到根本的.教師在某些試題的突破上可以通過專題的形式，強(qiáng)化一題多解、多題一解的訓(xùn)練.在解決問題的過程中，解題思路是如何形成的，解題方法是如何構(gòu)想的，這些對于學(xué)生來說都是至關(guān)重要的，我們應(yīng)該留給學(xué)生足夠的反思時間和“悟透“的空間.反思解題方法的探索發(fā)現(xiàn)過程，反思錯誤的成因及對策，反思處理問題的思維過程和數(shù)學(xué)思想方法，反思是否對問題進(jìn)行深入細(xì)致的分析轉(zhuǎn)化.學(xué)生通過回顧和總結(jié)解題思路，定能收到事半功倍的效果.學(xué)生在鉆研解決問題的基本方法之外，更深層次是能說明白問題考查的知識要點，以及問題的來源、問題設(shè)置的背景，這樣真正把所學(xué)的知識內(nèi)化，形成學(xué)生自己的學(xué)習(xí)技能，達(dá)到了取“漁”的目的.

4 改編賞析，思維拓展

通過上述對2016年浙江省數(shù)學(xué)高考理科第15題的分析和理解，筆者對該題進(jìn)行了如下改編：

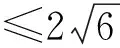
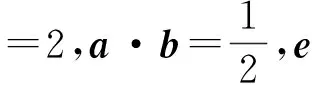
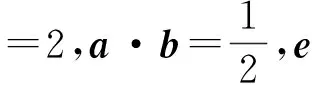
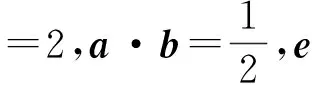
結(jié)束語 2016年的高考已經(jīng)結(jié)束，在高考中重點知識一定會重點考查，而平面向量知識仍然以作為考查學(xué)生創(chuàng)新思維的題目出現(xiàn).在求解平面向量試題時，要能夠練就以形助數(shù)和以數(shù)解形的雙重本領(lǐng).偉大數(shù)學(xué)家哈爾莫斯曾說過：問題是數(shù)學(xué)的心臟.數(shù)學(xué)的學(xué)習(xí)就是在不斷地提出問題和解決問題的過程中發(fā)展的.波利亞也說過：掌握數(shù)學(xué)就意味著善于解題，不僅善于解一些標(biāo)準(zhǔn)的題，而且善于解一些要求獨立思考、思路合理、見解獨到和有發(fā)明創(chuàng)造的題.學(xué)生在數(shù)學(xué)學(xué)習(xí)的過程中，領(lǐng)悟基本知識、基本方法的運用，通過引導(dǎo)學(xué)生歸納解題方法、技巧、規(guī)律和思想方法，促進(jìn)知識向能力轉(zhuǎn)變，實現(xiàn)自我完善，爭取達(dá)到“做一題通一法，會一類通一片”的效果.2016年的平面向量試題簡約但是不簡單，正所謂“大音希聲，大象無形”！

[1] 李學(xué)軍.用本促真 貼地前行[J].中學(xué)教研(數(shù)學(xué))，2016(4):27-30.

[2] 曹鳳山.講好數(shù)學(xué)背后的故事——解題教學(xué)的一項基本功[J].中學(xué)教研(數(shù)學(xué))，2016(6):1-4.

?2016-06-19；

2016-07-19

李學(xué)軍(1976-)，男，吉林德惠人，中學(xué)一級教師.研究方向：數(shù)學(xué)教育.

O123.1

A

1003-6407(2016)12-43-03