善于“捕捉”特征 尋找解題途徑*
●楊玉坡
(英雄山中學 山東泰安 271000)
?
善于“捕捉”特征 尋找解題途徑*
●楊玉坡
(英雄山中學 山東泰安 271000)
一個數學問題,往往表現出或隱含著諸如:數字、位置、圖形、結構、差異等特征,解題時若善于“捕捉”這些特征,則有利于尋找到快速解決問題的途徑.
捕捉;特征;尋找;解題;途徑
一個數學問題,無論是條件、結論,還是數字、直觀圖像、整體結構等,往往表現出或隱含著某種特征.解題時,若善于分析、捕捉這些特征,并由此進行分析、變換、聯想、構造,不僅有利于提高解題決策的敏捷性、尋找到快速解題的途徑,而且可以有效地優化問題解決的過程.下面從幾個方面來闡述,供參考.
1 “數字”特征
數學離不開“數字”,巧合的數字、共性的特征,看似偶然,往往暗含著對解題起導向作用的必然.只要善于觀察、分析,從數字本身的變化、數字與數字之間的聯系就能尋找解題的切入點[1].
例1 已知正數a,b滿足ab=4,求證:
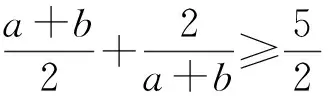


即
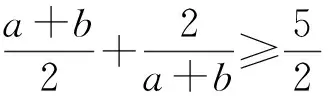


( )

(2012年重慶市數學高考文科試題第5題)
分析 17°,47°暗含了特征47°-17°=30°,也暗含了本題可轉化利用30°進行解題.


故選C.
點評 本題若分析不到位,則很難發現和利用數字(角)特征“47°-17°=30°”,從而解題思維受阻或無從下手.
2 “位置”特征
與圖形(像)有關的一些數學問題都有它特定的位置關系,從與眾不同的位置關系上尋找解題的切入點,可以明確解題方向,甚至可以收到不攻自破的解題效果.
例3 若直線y=kx+b是曲線y=lnx+2的切線,也是曲線y=ln(x+1)的切線,則b=______.
(2016年全國數學高考理科試題第6題)
分析 從2條曲線的公切線入手,建立方程組求解.
解 設曲線y=lnx+2上切點的橫坐標為x1,則切線方程為
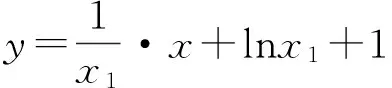
設曲線y=ln(x+1)上切點的橫坐標為x2,則切線方程為
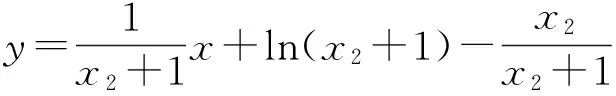
依題意可得
解得

故
b=lnx1+1=1-ln2.
點評 解決本題的關鍵是抓住“直線y=kx+b是2條曲線的公切線”這一位置特征.
例4 已知變量x,y滿足約束條件

若直線y=k(x-1)將可行域分成面積相等的2個部分,則目標函數z=kx-y的最大值為______.

圖1

z=kx-y=-3x-y.
平移直線-3x-y=0,易知當直線z=-3x-y經過直線x-y+3=0與直線x+y-1=0的交點C(-1,2)時,z=-3x-y取得最大值,且zmax=1.
點評 本題若不能夠發現直線恒過定點這一位置關系,則很難處理好直線y=k(x-1)將可行域分成面積相等的2個部分,也就無法順利解題.
3 “圖形”特征
一些抽象的數量關系,若轉化為具體的圖形問題,從圖形特征中尋找解題的切入點,則思路直觀、清晰,有利于快速解題.
( )


分析 若用代數方法,設出直線l的方程,與雙曲線方程聯立后,利用判別式Δ≥0求解,則過程冗繁.若充分利用圖形特征,則可使問題快速解決.
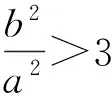
于是

即
e2>4,
亦即e>2.故選D.
點評 若能對所求數學問題既分析其代數含義又挖掘其幾何背景,也就是將抽象的數學語言與直觀的圖形結合起來,在代數與幾何的結合中找出解題思路,則十分方便.求解圓錐曲線的離心率時,常利用平面圖形的性質,利用圖形特征使問題化難為易.
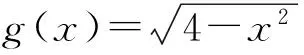
(2014年山東省數學高考理科試題第5題)

點評 本題將新定義的問題巧妙地遷移、轉化為“直線與圓的位置關系”問題求解,可以看出這種構造應用具有創造性.
4 “結構”特征
數學問題條件或結論中常常隱含著某種特殊的關系,善于洞察并加以分析、加工和轉化,可迅速找到問題解決的切入點.
例7 設x,y為實數,且滿足
則x+y=______.
分析 條件中2個方程左邊的結構形式相同,為此構造函數f(x)=x3+2 017x,并討論其單調性和奇偶性即可達到解題的目的.
解 由已知,方程組可變形為

f(x-1)=f(1-y),
即
x-1=1-y,
亦即
x+y=2.
點評 若按常規方法求解此題,難度較大,甚至無法入手.這里通過構造函數,利用函數的奇偶性和單調性轉化求解,方法巧妙,且過程簡潔.
1)求證:點P的縱坐標為定值,并求出這個值;
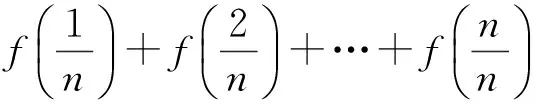
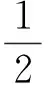
解 1)因為點P為P1P2的中點,所以

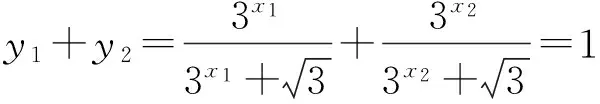

2)由x1+x2=1,得
y1+y2=f(x1)+f(x2)=1.



1+1+…+1+2f(1)=

即
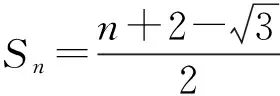
點評 本題在求和時,運用了第1)小題所得等式f(x)+f(1-x)=1得到通項的特征,即

由于距首末2項等距的2項相加和為定值,從而可以用倒序相加法求和.
5 “差異”特征
條件是解題的基礎和依據,結論是解題的目標.善于捕捉條件和結論之間的“差異”關系,并以此啟動和確定解題的切入點.

分析 條件中給出了2個“不等量”關系,結論探求的是“等量”關系.通過對這一差異 “點”的分析,獲知解題的切入點就是化“不等”為“等”.
解 因為Sn≤n2+n-1,所以
S1=a1≤12+1-1=1,
即a1≤1.
(1)


又a1>0,從而
(2)
故由式(1)和式(2)可得a1=1.
由Sn≤n2+n-1,即



(3)
因為
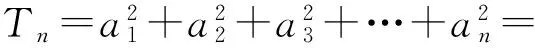
[12+22+…+(n-1)2]d2=
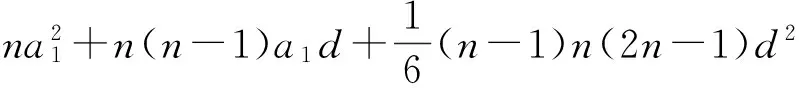


從而
(2n-1)d2+6d-8(n+1)≥0,
即
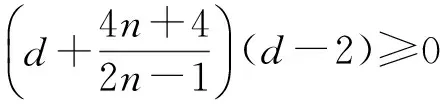
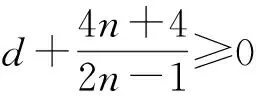
d-2≥0,
即d≥2,
(4)
故由式(3)和式(4)可得d=2.
點評 本題通過對“等”與“不等”的差異點進行分析和轉化,使得不等式中的夾逼法則(如果實數x,a滿足a≤x≤a(即x≥a且x≤a),則必有x=a)在本題中起了重要的作用.
[1] 尹承利.例說尋找解題切入點的途徑[J].中學數學研究,2003(5):25-27.
?2016-09-30;
2016-10-31
楊玉坡(1981-),男,山東泰安人,中學一級教師.研究方向:數學教育.
O122
A
1003-6407(2016)12-18-04

