基于SVR－IPSO的高危行業企業安全投入優化模型及其改進
——以煤炭生產企業為例

王金鳳陳 贊翟雪琪馮立杰，2

1（鄭州大學，鄭州 450001）2（河南省煤層氣開發利用有限公司，鄭州 450016）

基于SVR－IPSO的高危行業企業安全投入優化模型及其改進
——以煤炭生產企業為例

王金鳳1陳 贊1翟雪琪1馮立杰1，2

1（鄭州大學，鄭州 450001）2（河南省煤層氣開發利用有限公司，鄭州 450016）

傳統的安全投入模型對解決高危行業領域中模糊復雜的安全投入問題具有一定局限性，尤其當建立目標函數時，采用隱含線性關系假設的函數進行擬合會影響模型的推廣能力 。基于此，本文首先采用支持向量回歸機（SVR）建立事故損失模型，與傳統C－D函數擬合結果相比，該模型具有更好的預測能力；然后，以實際安全投入要求為約束，以安全總成本最小化為原則建立企業安全投入優化模型 ；最后，采用基于捕食搜索策略的粒子群算法對模型進行求解，同時，為保證全局收斂性，引入自適應控制策略對算法進行了改進。結果表明：該模型能夠更加準確地描述安全投入與安全成本間的非線性作用關系，并通過粒子群尋優得到具備可行性的全局最優解，為高危行業企業安全投入結構優化提供新的決策思路 。

安全 高危行業 SVR 捕食搜索算法 自適應控制

引 言

我國高危行業企業是指參與高危行業運營的企業或組織，如煤礦、非煤礦山、建筑施工行業、危險化學品行業等企業，該類企業為實現安全生產，必須進行安全投入，以降低安全事故帶來的損失。然而，由于我國高危行業企業普遍存在安全投入決策不科學、結構不合理等現象，使得有限的安全投入并未得到充分利用，在造成資源浪費的同時也增加了安全隱患及事故發生概率，導致事故損失成本激增，為企業帶來了沉重的經濟負擔。因此，如何優化高危行業企業安全投入結構，降低事故損失，減少安全生產成本的投入成為亟待解決的現實問題。

對此，已有學者進行了相關研究。陸寧等［1］針對建筑施工企業的特點，分析了影響該類企業安全水平的重要投入指標，并建立了安全投入指標綜合重要度評價模型；Wang等［2］采用DEA（數據包絡分析）方法綜合評價了煤礦安全投入產出效率 ；李廣龍等［3］結合我國歷年投入產出數據構建DEA模型，并采用Malmquist指數（全要素生產力指數）對煤礦安全投入效率進行了深入分析；Tong等［4］提出了煤礦生產、安全投資系數以及事故消耗系數的計算方法并建立了煤礦安全動態投入產出模型；董大旻［5］等采用因子分析法提煉出建筑企業投入6要素，并結合EFQM（業務卓越模型）構建了建筑企業安全投入績效評價結構方程模型（SEM）；丁日佳等［6］分析了煤炭生產與安全水平間的影響關系，根據多項式回歸擬合分析，構建了煤炭安全生產模型；任海芝等［7］將安全投入準則層分為預防性和損失性兩部分，根據C－D生產函數擬合安全總投入與各指標間的關系，建立了以安全總投入最小化為目標的優化模型。

現有關于安全投入的研究多集中在指標評價、效率優化等方面，已有的涉及到安全投入優化的研究，其模型中目標函數的構建多采用多項式回歸、邏輯回歸等方法，該類方法通常隱含著線性關系的假設，而高危行業領域數據收集困難、數據量小，且數據間具有模糊復雜的非線性關系［8］。因此，采用常規方法分析安全投入優化問題存在一定的局限性。

綜上，本文提出了一種高危行業企業安全投入優化的改進模型。采用支持向量回歸機（SVR）擬合變量間復雜的作用關系。SVR是一種機器學習方法，它在解決小樣本、非線性、高維和局部極小點等實際問題中有著獨特優勢［9］。借助SVR的特點構建的安全投入優化模型能夠更好地解釋小樣本數據間的非線性規律。針對模型的求解，作者將采用粒子群優化算法（PSO）尋找模型最優解，與其他進化算法相比，PSO具有精度高、易實現等優勢［10］。同時，為保證全局收斂性，引入捕食搜索策略及自適應控制對該算法進行改進。最后，通過實證分析了該方法的可行性及有效性。

1 基于SVR的事故損失模型分析

企業安全成本包括安全投入及事故損失兩部分。其中，安全事故損失與企業當年的安全投入規模和結構密切相關，在探究它們之間的作用關系時，為克服傳統方法的不足，可采用SVR構建安全事故損失模型，為后續構建安全投入優化模型提供基礎。

1.1 SVR理論描述

當支持向量機用于回歸估計時稱為支持向量回歸機（SVR），其基本思想是：對于訓練樣本集（xiyi） （其中i＝1，2，3，…，l；xi∈Rm為輸入變量；yi∈R為對應的輸出值），尋找一個輸入空間到輸出空間的非線性映射φ，并通過將數據x映射到一個高維特征空間F來求解最優回歸函數。SVR回歸模型可表述為：

其中，g為核函數參數，其控制著核函數的徑向作用范圍，數值大小影響著模型的泛化能力。

由SVR原理可知，適當的選取懲罰系數c和核函數參數g對回歸模型的效果起重要作用。

1.2 基于SVR的事故損失模型構建

有鑒于高危行業企業生產作業的特殊性，事故隱患伴隨其生產過程的始終。為改善安全生產狀態，遏制事故發生減少事故損失，企業往往進行必要的安全投入。

由于各安全投入要素與事故損失間存在模糊、復雜的非線性關系，因此，在研究它們之間的作用機理時，為克服傳統方法的不足，可以采用SVR構建安全事故損失模型L＝f（x1，x2，…，xn）。

以煤炭生產企業為例。由于煤炭生產過程復雜，環境特殊，由人員操作失誤、設備損壞、管理疏忽等原因易導致安全事故的發生［11］。因此，煤炭生產企業更加重視對安全的投入。根據各投入要素功能的差異，可將安全投入分為人員素質x1、機械設備x2、環境改善x3、安全管理x4、應急預防x5五方面內容［12］。

不同煤炭生產企業的安全水平有所區別，但影響安全生產的重要因素與安全生產間的作用規律是一致的。正是由于企業間存在安全狀態的差異，更有利于從中找出影響安全生產的制約因素。因此，本文從大樣本中隨機挑選15家中小型煤炭生產企業在2013～2015年間的安全投入情況作為輸入變量，事故損失情況作為輸出變量，共獲得45組樣本數據，隨機選出40組作為訓練樣本，其余5組作為測試樣本驗證模型的有效性。采用LIBSVM工具箱中回歸與參數尋優功能構建基于SVR的事故損失模型，并將預測樣本的輸出結果與傳統C－D函數擬合結果作對比，驗證模型的推廣能力。具體流程如圖1所示。xi為訓練樣本輸入數據向量；xj為分析樣本輸入數據向量；K（xi，xj）為核函數。

根據Mercer條件可定義核函數，本文選用徑向基核函數（RBF）：

圖1 事故損失模型構建流程圖

（1）為獲得更好的SVR擬合效果，將樣本數據進行歸一化處理。同時，由1.1節可知，在運用支持向量機進行回歸分析時，參數c、g的選擇至關重要。因此，在使用LIBSVM工具箱建模前，需要采用網格搜索進行參數尋優，關鍵編程語言如下：

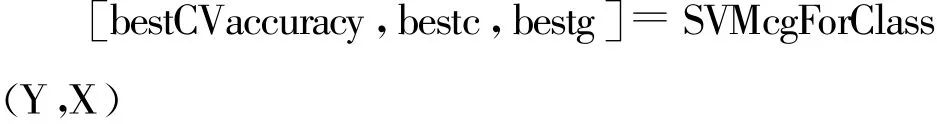
其中，Y表示損失值數據集，X表示安全投入數據集。經過參數尋優過程得到參數c、g的值分別為6.519，24.949。

將參數c、g代入式（1）、（2）經過支持向量機回歸訓練，得到基于SVR的事故損失模型，如下：

（2）傳統的事故損失模型采用C－D函數擬合安全投入與事故損失間的作用關系，表示形式如下：

對上式左右兩邊同時取對數，可轉化為如下形式：

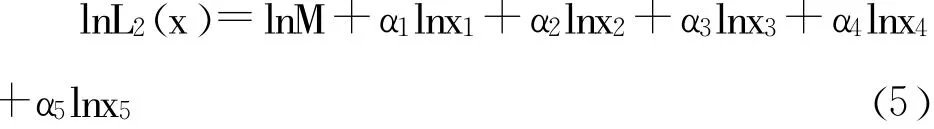
將訓練樣本取對數，采用MINITAB軟件進行多元線性回歸，可得事故損失與各分項安全投入之間的函數關系，見式（6）。

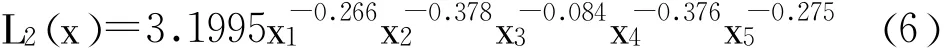
利用均方誤差RMSE和平方相關系數R2可以評價兩種模型的擬合性能，SVR模型和C－D模型的擬合誤差如表1所示。

表1 擬合誤差對比

為進一步驗證模型的推廣能力，將5組測試樣本分別代入兩種模型，預測曲線見圖2。

圖2 預測曲線圖

由表1可以看出，兩種方法的平方相關系數R2基本相同，但C－D函數擬合的均方誤差值明顯大于SVR模型的對應值，表明基于SVR參數尋優方法對事故損失額與安全投入兩者間的擬合效果要優于C－D函數的擬合效果。而且，從圖2的預測曲線對比圖中可以觀察到，采用SVR模型的預測效果更接近于真實值。

進一步分析，對C－D函數取對數后發現變量間呈現線性關系，且擬合式中并未體現出變量之間的交互作用，因此，采用C－D函數來解釋數據間隱含的復雜關系時，會出現擬合效果和預測效果不佳的情況。

基于此，本文將基于SVR擬合所得式（3）作為確定安全成本中事故損失值的計算模型，為安全投入優化模型中目標函數的構建提供依據。

2 安全投入優化模型的構建

以上述SVR擬合模型為基礎確定安全投入與安全總成本之間的函數關系，并以總成本最小化為原則構建安全投入優化模型，為高危行業企業優化安全投入結構提供方法支持。

2.1 目標函數的確定

高危行業企業為實現安全生產，會投入必要的安全成本，同時，期望用最小的安全成本獲得最大的安全效益。企業安全成本既包括為保障安全生產所進行的安全投入，還包括事故發生后所造成的事故損失［13］。以安全成本投入G最小化為模型的目標函數：

式中：L≥0為事故損失值，其表達式為（3），萬元；C為各項安全投入總和，，萬元；xi（i＝1，2，…，n）為各項安全指標投入量，萬元。

2.2 約束條件的確定

企業為追求利益的最大化，不會無限增加安全投入，企業能夠承擔的最大安全投入規模即安全投入上限U。

此外，受到行業制度規范的約束，企業必須承擔的最小安全投入規模即安全投入下限D，即：

安全投入優化的前提條件是保證各項指標的最低要求得到滿足，以防止由于投入不足造成的安全隱患。同時，考慮到某些指標間具有相互聯系、相互影響的關系，在設定投入下限時，需要綜合考慮某幾項指標間的投入情況，即：

綜上，可將安全投入優化模型表述為：

3 基于IPSO的安全投入優化模型求解

采用SVR擬合事故損失和安全投入間的作用關系，進而構建安全投入優化模型，能夠提高模型的推廣能力，但同時也加大了模型的復雜程度，而利用傳統的求解方法很難尋找到最優解，因此，可采用基于捕食搜索策略的粒子群（PS－PSO）求解模型最優值，同時為防止粒子搜索時出現越過最優解的現象，引入自適應控制對該方法進行改善，得到改進的PS－PSO算法，也即IPSO算法。

3.1 PS－PSO算法

捕食搜索是一種模仿動物捕食搜索行為的空間搜索算法。采用捕食搜索算法尋優時，首先需要在搜索空間整體范圍內進行全局搜索，找到較優解，然后在較優解周圍進行局部搜索，若未找到更優解則選擇放棄在該區域的搜索工作，并返回全局搜索步驟，繼續尋找較優解。如此循環直至搜索到最優解（或接近最優解）后停止搜索。

基于捕食搜索的PSO算法是對標準PSO算法中粒子搜索方式進行改善。對于粒子在n維搜索空間中第i個粒子的飛行速度Vi＝（vi1，vi2，…，viD）和距離Pi＝（pi1，pi2，…，piD）的計算公式不作改變，見式（11）、（12）。

式中：i＝1，2，…，m ；c1、c2為非負常數；ξ、η是介于［0，1］之間的隨機數；w為慣性權重，是介于［0，1］之間的常數；k為迭代次數；

需要說明的是：在粒子群尋優過程中，每個粒子的位置代表一個潛在解，初始粒子需要在不斷的迭代中完成尋優任務，在此過程中，第i個粒子在 n維搜索空間的位置為Xi＝（xi1，xi2，…，xiD），計算第i個粒子的適應度值，并與兩類 “極值”作比較，即局部極值Pi（也即Pbest）和Pg全局極值（也即Gbest），進而完成對自身位置的更新。

3.2 改進PS－PSO算法（IPSO）

捕食搜索可以通過控制搜索空間范圍大小，完成全局搜索與局部搜索之間的相互轉換，具備良好的局部集中搜索和跳出局部最優的能力，這正是標準PSO算法所欠缺的。然而，當解決復雜非線性尋優問題時，由于搜索范圍隨機生成，固定的搜索速度易導致粒子搜索時越過最優解，從而陷入局部最優。

因此，本文在常規PS－PSO基礎上引入自適應控制策略，對粒子速度進行變異，即對式（12）進行如下調整：

式中：δ為調節參數；j為范圍限制，每個范圍限制下進行c次重復搜索；i為當前迭代次數；maxi為各范圍限制對應的最大迭代次數。

當粒子在較大的范圍限制內進行搜索時，粒子速度較快，使算法能夠快速尋找到較優解，接著，粒子將以此較優解為中心進行小范圍的搜索，受到算法的約束，粒子速度逐漸變緩，以保證在較優解周圍尋找更優解的搜索精度。由于粒子搜索速度受到當前迭代次數的影響，因此，可以使粒子速度得到有效的調節。為防止陷入局部最優，算法將在無法找到更優解時重新生成范圍限制對全局進行搜索。

結合以上對IPSO算法的描述，可以得到安全投入優化模型求解的具體過程為：

步驟1：根據實際要求確定安全投入優化模型的目標函數及約束條件，構建安全投入優化模型；

步驟2：初始化設置，隨機產生種群和速度，計算初始最優解Gbest；

步驟3：將改進的（13）式替代（12）式作為標準PSO算法中的位置更新公式。以當前最優解為中心，在當前限制L下重新隨機初始化粒子，進行迭代尋優，得到一個歷史最優解Pg，若Pg＜Gbest，則Gbest＝Pg，重復此步驟；

步驟4：若在當前限制L下重復c次搜索后，無較優解，則在限制L＋1的基礎上重新初始化粒子進行搜索，若得到更優解則轉至步驟3，否則重復本步驟；

步驟5：在對所有限制區域完成搜索后，輸出最優結果，對應的最佳粒子位置向量即安全投入的最終優化方案。

4 實證分析——以煤炭生產企業為例

本文選取某煤業集團下屬煤炭生產企業Y為實證對象，以檢驗模型的可行性及有效性。Y企業生產能力為60萬噸/年，根據國家安全生產監督管理總局頒發的 《企業安全生產費用提取和使用管理辦法》［14］中相應費用的規定，當煤礦年產量為60萬噸時，煤礦的安全資源投入最低應為D＝300萬元。該企業在2015年的安全總成本為630萬元，計劃要將2016年的安全成本控制在U＝600萬元以內，包括事故損失投入和安全投入（人員素質x1、機械設備x2、環境改善x3、安全管理x4以及應急預防x5）。

考慮到安全投入的某些指標間具有相互聯系、相互影響的關系，結合該企業實際，構建安全投入優化模型：

其中，式（14）表示安全投入成本最小，L≥0為事故損失值，其表達式是由1.2節中基于SVR擬合所得式（3）構成；式（15）表示總體安全投入的上限和下限；式（16）表示人力與設備是煤礦生產的關鍵生產要素，其投入不僅要滿足生產要求，還要滿足最低安全投入要求；式（17）表示對人為安全因素的外部約束，包括設備、環境及管理約束；式（18）式表示為保證事故發生后的應急環節正常運轉需要滿足的最低安全投入要求。

本文利用Matlab編程實現對上述模型的求解。首先需要進行參數設置，標準PSO算法中常規參數包括［15］：慣性權重w，常數系數c1、c2。

當引入改進PSO算法后，需要進一步根據反復實驗的結果確定調節參數δ，重復搜索限制c，最大迭代限制maxi，以保證粒子具有較好的搜索能力，具體參數設置如表2所示。

其次，分別采用常規PS－PSO和改進粒子群算法（IPSO）對安全投入優化模型進行求解，可以得到尋優對比結果，見表3。

表3 PS－PSO與IPSO 優化結果對比

由表3可知，本文提出的IPSO算法的計算結果優于PS－PSO的計算結果。由于在PS－PSO的基礎上，引入了捕食搜索及自適應控制算法，很好地克服了PS－PSO算法在搜索過程中易出現越過最優解的問題，從而保證計算結果達到了全局最優。

最后，根據最佳粒子位置確定該企業在2016年的安全投入優化方案為xT＝（80.3，106.7，58.8，120.3，60.8）萬元，對應的安全總成本為509.3萬元，與2015年相比降低了19.2%。

5 結 論

本文針對傳統安全投入模型的局限性，提出了安全投入優化改進模型，以解決高危行業企業的安全投入問題。采用SVR能夠克服了傳統方法在擬合時隱含線性關系假設的不足，提升了模型中目標函數的推廣能力，但同時也增加了目標函數的復雜程度。因此，在對模型進行求解時，為保證全局收斂性，本文引入自適應控制算法對常規PS－PSO進行了改進。

結果表明，該模型能夠較準確地描述安全投入與安全成本間的非線性作用關系，并通過粒子群算法尋優得到具備可行性的全局最優解，以期為高危行業企業制定安全投入優化策略提供更加準確的理論依據。

［1］陸寧，劉楠，張煥芳，等 .建筑施工企業安全投入指標的綜合重要度診斷 ［J］.工業安全與環保，2014，（1）：73～75

［2］Wang Shu－Ming.Evaluation of Safety Input－Output Efficiency of Coal Mine Based on DEA Model［J］.Procedia Engineering，2011，26：2270～2277

［3］李廣龍，周科平，侯造水.基于DEA和Malmquist指數的煤礦安全投入效率評價 ［J］.中國安全生產科學技術，2014，（11）：162～167

［4］Tong Lei，Wang Liangyu，Ding Rijia，Liu Lijia.Study on the Dynamic Input－Output Model with Coal Mine Safety［J］.Procedia Engineering，2011，26：1997～2002

［5］董大旻，馮凱梁 .基于EFQM的建筑企業安全投入績效評估SEM ［J］.中國安全科學學報，2012，（2）：10～16

［6］丁日佳，劉娜 .我國煤礦生產與安全投入的計量分析 ［J］.工業安全與環保，2015，（7）：86～88

［7］任海芝 ，陳玉琴 ，程戀軍.煤炭企業安全投入規模與投入結構優化研究 ［J］.中國安全科學學報，2014，（8）：3～8

［8］Azadeh，V.Salehi，M.Arvan，M.Dolatkhah.Assessment of Resilience Engineering Factors in High－risk Environments by FuzzyCognitive Maps：A Petrochemical Plant［J］.Safety Science，2014，68：99～107

［9］Yassine Ben Salem，Salem Nasri.Automatic Recognition of Woven Fabrics Based on Texture and Using SVM［J］.Signal，Image and Video Processing，2010，4（4）：429～434

［10］杜軍崗，魏汝祥，劉寶平 .基于PSO優化LS－SVM的小樣本非線性協整檢驗與建模研究 ［J］.系統工程理論與實踐，2014，（9）：2322～2331

［11］郭凱.煤礦事故風險集成管理研究 ［J］.中國煤炭，2015，（7）：30～33

［12］王金鳳，翟雪琪，馮立杰.面向安全硬約束的煤礦生產物流效率優化研究 ［J］.中國管理科學，2014，（7）：59～66

［13］高蕊 .煤礦安全投入優化數學模型研究及應用 ［J］.中國煤炭，2012，（3）：105～108

［14］企業安全生產費用提取和使用管理辦法［J］.交通財會，2012，（4）：93～97

［15］李昌兵，杜茂康，付德強.基于層次粒子群算法的非線性雙層規劃問題求解策略 ［J］.系統工程理論與實踐，2013，（9）：2292～2298

Safety Investment Optimization Model of High Risk Industry Enterprises Based on SVR－IPSO and Its Improvement——A Case Study of Coal Production Enterprises

Wang Jinfeng1Chen Zan1Zhai Xueqi1Feng Lijie1，2
（1.Zhengzhou University，Zhengzhou 450001，China；2.Henan Provincial Coal Seam Gas Development and Utilization CO.，LTD，Zhengzhou 450016，China）

Input the traditional security model for solving the fuzzy and complex safety investment problem in high－risk industry has certain limitations.Especially when establishing the objective function，to use a function implied linear relationwill affect the model’s generalization ability.Based on this，this paper firstly used the support vector regression machine（SVR）to establish the accident loss model，compared with the traditional C－D function fitting results，the model had a better predictive ability；then，taking the actual security investment requirements as the constraint and the minimize safety cost as the principle，this paper established the enterprise security investment optimization model；finally，the model was solved by particle swarm optimization algorithm based on predatory search strategy.At the same time，in order to guarantee the global convergence，the algorithm was improved by introducing the adaptive control strategy.The results showed that the model could more accurately describe the nonlinear relationship between safety input and safety cost，and the particle swarm optimization algorithm to get the global optimal solution.This study provided a new decision－making method to optimize the safety investment structure of high risk industries.

high risk industry；safety input optimization；SVR；prey search algorithm；adaptive control

10.3969/j.issn.1004－910X.2016.12.016

F275

A

（責任編輯：史 琳）

2016—05—13

基金項目：國家自然科學基金資助項目（項目編號 ：71271194）；國家自然科學基金資助項目（項目編號：71472171）。

王金鳳，鄭州大學管理工程學院教授，博士。研究方向 ：煤礦物流工程、工業工程、煤礦災害救治等。陳贊，通訊作者，鄭州大學管理工程學院碩士研究生。研究方向：企業管理。翟雪琪，鄭州大學管理工程學院博士研究生。研究方向：安全管理、技術創新。馮立杰，鄭州大學管理工程學院教授，河南省煤層氣開發利用有限公司副總經理。研究方向：工業工程、技術創新。