Spar平臺垂蕩-縱搖與月池內流體垂向振動的耦合運動研究

劉利琴， 邱 雨， 張永恒， 唐友剛

(天津大學 水利工程仿真與安全國家重點實驗室，天津 300072)

?

Spar平臺垂蕩-縱搖與月池內流體垂向振動的耦合運動研究

劉利琴， 邱 雨， 張永恒， 唐友剛

(天津大學 水利工程仿真與安全國家重點實驗室，天津 300072)

考慮半開口月池，研究桁架式Spar平臺垂蕩、縱搖、月池內流體垂向振動的耦合運動。建立了平臺垂蕩-縱搖-月池內流體垂向振動的耦合運動方程，推導了月池內流體對平臺垂蕩和縱搖運動產生的力和力矩。針對三種工況，即不考慮月池開口、月池開孔率為30%和70%，數值計算了耦合系統的運動響應，分析了月池內流體對平臺垂蕩和縱搖運動的影響，結果表明，月池內流體對平臺主體垂蕩有抑制作用，且抑制程度與月池開孔面積有關；對于70%的開孔率，平臺垂蕩響應RAO曲線在月池流體垂向振動固有周期附近出現高頻峰值；70%開孔率時，月池內流體的運動遠大于30%開孔率的情況；考慮月池開口后，平臺的縱搖響應變化較小。最后，分析了耦合參數對平臺及月池內流體運動的影響。

Spar平臺；半開口月池；垂蕩-縱搖耦合；耦合參數分析

隨著Spar平臺作業水深的不斷增大，人們對平臺運動預報的精確度提出了更高要求。目前對Spar平臺主體、系泊系統與立管之間的耦合運動以及平臺主體各自由度之間的相互耦合問題進行了研究[1-3]，關于Spar平臺月池內部流體的運動及平臺主體與月池流體之間的相互耦合運動考慮較少。Spar平臺的中央井自下而上貫穿整個主體，其內按照一定的方式布置立管和其它重要鉆井設施，構成Spar平臺的月池。根據實際要求，有時將月池設計為半開口形式，海水可以自由進入或者流出月池。若采用頂張緊立管系統，則月池海水質量與平臺主體質量量級相當，月池內流體對平臺主體運動的影響不可忽略[4]。

BARREIRA等[5]研究了重力式平臺混凝土立柱與其月池內部海水的耦合運動，將月池流體運動處理為彈簧-質量系統，考慮月池流體質量的變化，建立了立柱與月池海水的耦合運動模型，分析了耦合系統的振動特性。SPHAIER等[6]基于模型試驗研究了單柱式平臺與月池內流體的耦合運動，測試了月池底部不同導向板面積時平臺的垂蕩運動，分析了導向板面積對平臺垂蕩的影響。GUPTA等[4]建立了Spar平臺垂蕩與月池流體垂向振動耦合的二自由度模型，研究了系統響應特性。結果表明，月池流體運動嚴重影響平臺的垂蕩運動，考慮月池的耦合影響時，平臺的運動形式非常復雜，具體形式與平臺運動周期、月池流體振動周期以及波浪周期有關。ZHOU等[7]基于線性勢流理論，研究了帶月池的柱狀結構的橫蕩、縱搖和垂蕩運動，結果表明，月池對垂蕩運動影響較大。劉利琴等[8-9]基于模型實驗和數值模擬相結合的方法研究了Spar平臺月池內流體與平臺垂蕩的耦合運動，分析了月池內流體對平臺垂蕩運動的影響。SEAN等[10]考慮月池的影響，研究了作業過程中浮筒接近轉塔時FPSO系統的時域響應。LIU等[11]采用特征函數匹配法，計算了帶月池的柱狀結構的水動力參數。

本文考慮半開口月池，考慮月池內流體垂向運動的耦合研究桁架式Spar平臺垂蕩-縱搖運動，根據可變形控制體質量守恒定律及動量守恒定律建立了月池內流體垂向運動方程，分析了月池內流體對平臺運動的影響及耦合參數對平臺和月池內流體運動的影響。

1 耦合動力學方程建立

1.1 平臺主體垂蕩-縱搖耦合運動方程

考慮恢復力、阻尼力、波浪力、系泊纜提供的恢復剛度、月池內流體的作用力， 以平臺重心為坐標原點，Spar平臺的垂蕩、縱搖耦合運動方程可表示為[12]：

(1)

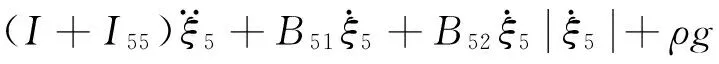
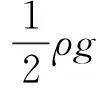
(2)

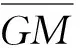
1.2 月池內流體的垂向運動方程

月池內部流體的運動形式可分為兩種，一種是沿月池垂向的活塞振動，另一種是在橫向的左右晃蕩運動，本文考慮月池內部流體的垂向運動與平臺主體運動的耦合。描述月池內部流體運動的坐標如圖1所示，其中，d0為平臺吃水，ξ為月池內流體的垂向位移，Smp為月池截面積，Sg為擋板的開口面積。

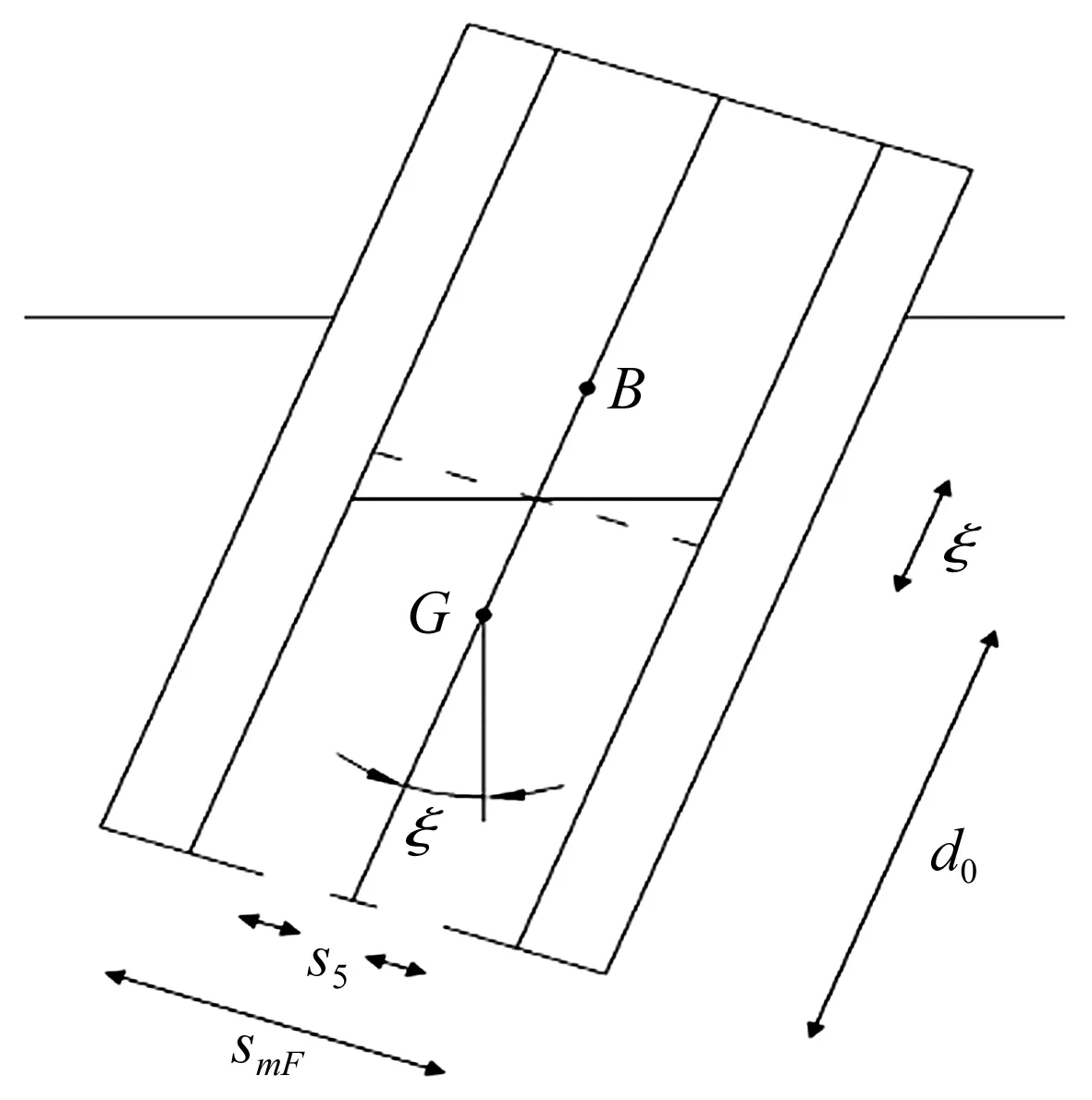
圖1 月池內流體運動坐標Fig.1 The coordinate of fluid motion in the moon pool

月池內流體的質量為：

Mmp=ρSmp(ξ+d0-ξ3cosξ5)

(3)

根據月池內流體的質量守恒定律，可以得到：

(4)

(5)

進一步求解式(5)，有：

(6)

根據月池內部流體的動量守恒定律，即作用在控制體上外力的合力與單位時間內通過控制面流入控制體內的動量之和等于單位時間內控制體中動量的增量，有：

(7)

(8)

(9)

(10)

(11)

將式(9)～式(11)代入式(7)中，有：

-ρg(ξ+d0-ξ3cosξ5)Smp+p1Smp

(12)

假設平臺做小幅縱搖運動，令cosξ5=1，由式(12)可以求得：

(13)

月池擋板的下表面壓力包括靜水壓力、垂蕩加速度產生的慣性力及入射波產生的動水壓力，寫為如下的半解析半經驗公式[4]：

(14)

式中:α3為平臺主體對月池的質量耦合系數；dg為擋板開口的等效直徑；pw為作用在擋板處的波浪壓力；ps為靜水壓力。

根據牛頓定理，對月池擋板開口處的流體建立力平衡方程，有：

(15)

式中:Kg為擋板開口流體運動的阻尼力系數；α1為月池附加質量系數。將式(13)和式(14)代入式(15)，整理后得到月池內流體的垂向運動方程為：

(16)

聯立式(1)、式(2)和式(16)，即得到月池內流體的垂向運動與平臺主體垂蕩-縱搖耦合的運動方程。

1.3 月池內流體對平臺的作用力(矩)

本文考慮月池內流體對平臺垂蕩和縱搖運動的作用力。月池內流體在垂蕩方向對平臺的作用力根據2.2節中擋板受力的力平衡方程求解，可表示為：

(17)

式中:Fc為修正項，其形式可用如下經驗公式表示[4]：

(18)

式中:α4為月池對平臺主體的質量耦合系數。

平臺搖擺運動時，可將月池內流體分為兩部分，即接近上部自由液面隨平臺搖擺發生晃動的部分和月池下部相對平臺靜止的部分。根據貯液容器內液體的晃蕩理論，將月池內流體的晃動等效為單擺，相對平臺靜止的部分等效為固定在平臺上的質量快。當平臺以Ψ0sinΩt的形式縱搖時，月池內流體對平臺的縱搖力矩為[13]：

(19)

式中:h為月池內水深；m0和I0分別為相對平臺靜止的流體質量及其對自身質心的轉動慣量；mn為第n階單擺質量；ln為第n階單擺的擺長；mn、ln、Ln和m0的表達式如下：

(i=1,2,…)

(20)

(i=1,2,…)

(21)

(i=1,2,…)

(22)

(23)

式(19)～式(22)中，L為月池寬度，M為月池內流體的總質量。

1.4 平臺主體波浪力

基于微幅波理論計算平臺受到的一階波浪載荷。根據文獻[14]的推導，得到規則波作用下平臺受到的一階垂蕩激勵力和縱搖激勵力矩分別為：

Fw=2ρghwSp

(24)

(25)

式中:R為平臺主體半徑；Hw為波高；k為波數；ω為波浪頻率；J1(kR)和Y1(kR)分別是第一類和第二類一階Bessel函數，β1和β2的表達式如下：

(26)

(27)

式(27)中，′表示求一階導數。

2 平臺參數

以Horn Mountain Spar平臺為基礎進行分析[15]，該平臺由BP石油公司在墨西哥灣安裝并工作，工作水深達到1 646 m，在開放式平臺主體上裝有三層垂蕩板結構，并通過9條系泊纜定位，主體結構示意圖見圖2。原始的Horn Mountain平臺采用浮力罐來支撐立管，底部為封閉月池。本研究將浮力罐改為頂部張緊器，考慮三種不同的月池底部形式，即0%開口(全封閉，工況1)、30%開孔率(工況2)及70%開孔率(工況3)，見圖3，平臺參數見表1。

圖2 整體結構示意圖Fig.2 Diagram of overall structure

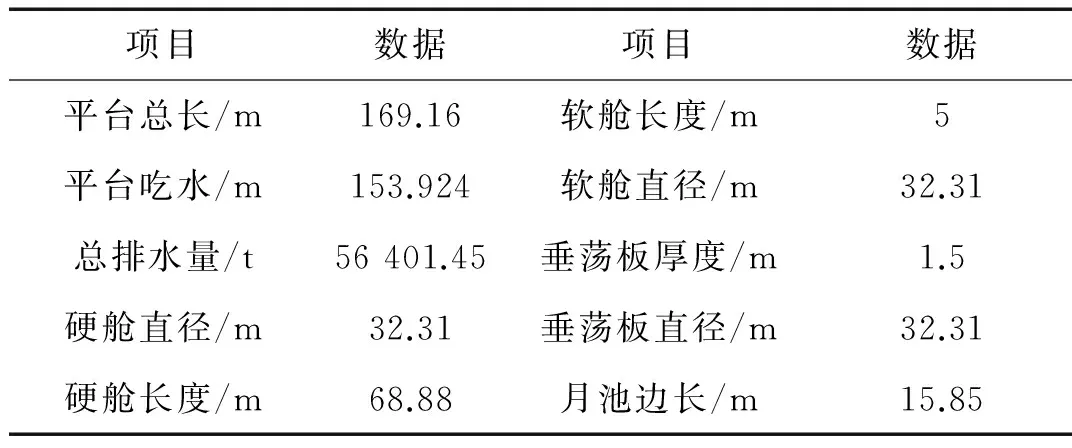
項目數據項目數據平臺總長/m169.16軟艙長度/m5平臺吃水/m153.924軟艙直徑/m32.31總排水量/t56401.45垂蕩板厚度/m1.5硬艙直徑/m32.31垂蕩板直徑/m32.31硬艙長度/m68.88月池邊長/m15.85

圖3 不同開口率的月池示意圖Fig.3 Diagram of moon pool of different opening ratios

文獻[8]開展了該平臺三種不同工況的模型試驗，本文在文獻[8]的基礎上，進一步計算了不同工況時平臺垂蕩、縱搖運動的周期和阻尼系數。對于桁架式Spar平臺，垂蕩運動的非線性阻尼(黏滯阻尼)遠大于線性阻尼，以下分析中只考慮了非線性垂蕩阻尼。平臺垂蕩和縱搖運動的周期及阻尼系數如表2和表3所示。

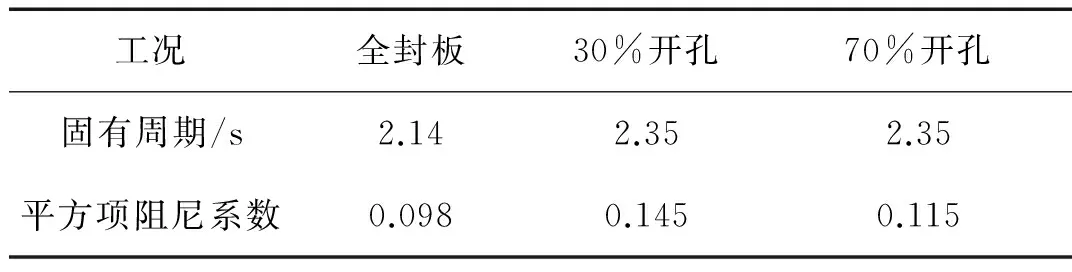
表2 垂蕩周期及阻尼系數

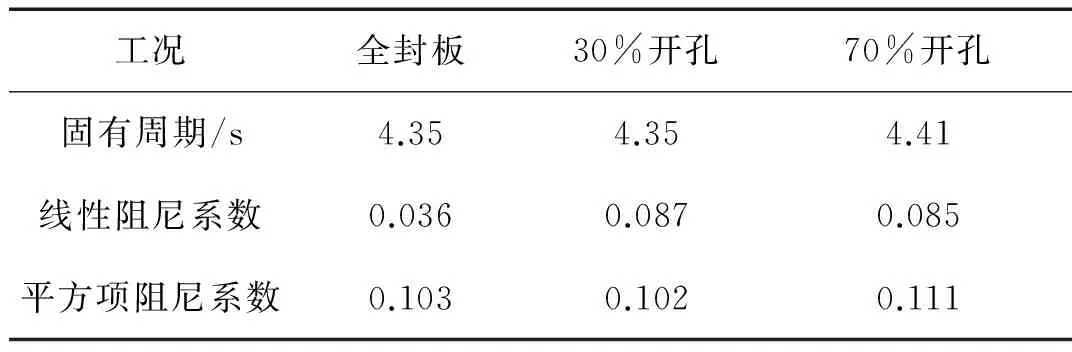
表3 縱搖周期及阻尼系數

表2和表3結果表明，考慮月池底部開孔后，平臺阻尼和固有周期增加，月池開口后對平臺垂蕩模態的運動特性影響較大。與全封板情況相比較，30%開孔率時垂蕩阻尼增大約48%，70%開孔率時垂蕩阻尼增大約18%。

3 計算結果及分析

3.1 運動響應分析

利用Runga-Kuta方法數值求解式(1)、(2)和式(16)，其中阻尼系數由表4和表5獲得，其它參數為α1=0.326、α3=0.5、α4=0.5及Kg=1.0。針對三種工況進行分析，即全封板、30%開孔率和70%開孔率，計算不同波浪周期時耦合系統的運動響應，得到三種工況平臺垂蕩、縱搖及月池內流體垂向運動響應的RAO曲線，圖4～圖6所示。

圖4 平臺垂蕩RAO曲線Fig.4 RAO curves of platform heave

圖5 平臺縱搖RAO曲線Fig.5 RAO curves of platform pitch

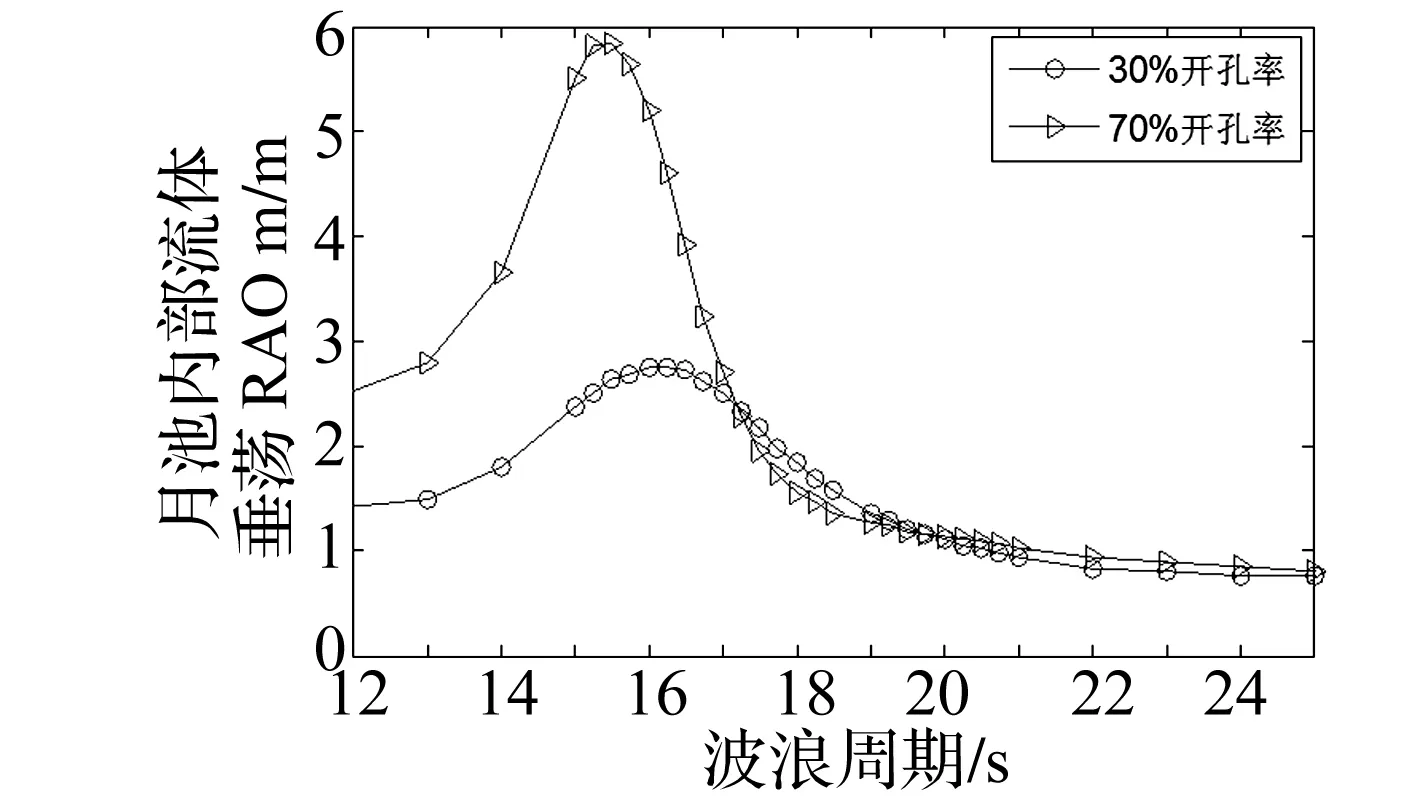
圖6 月池內部流體垂向運動RAO曲線Fig.6 RAO curves of fluid motion in the moon pool in the vertical direction

圖4～圖6表明，考慮半封閉月池后，在波浪周期接近垂蕩固有周期時，月池流體對平臺主體垂蕩有抑制作用，且抑制程度與月池開孔面積有關，本文計算中30%開孔率時平臺的垂蕩運動響應較小。另外，70%開孔率時，平臺垂蕩的RAO曲線在月池內部流體固有周期附近出現低頻共振峰，月池內流體的運動遠大于30%開孔率時月池內流體的運動。考慮月池開口后平臺的縱搖響應變化較小。

3.2 參數敏感性分析

針對30%開孔率和70%開孔率兩種情況，分析了月池附加質量α1、平臺對月池的質量耦合系數α3及月池對平臺的質量耦合系數α4分別對月池內流體運動及平臺垂蕩運動的影響，結果如圖7～圖12所示。

圖7 α1對月池內流體的運動影響分析Fig.7 The analysis of the effect of α1to the fluid motion in the moon pool

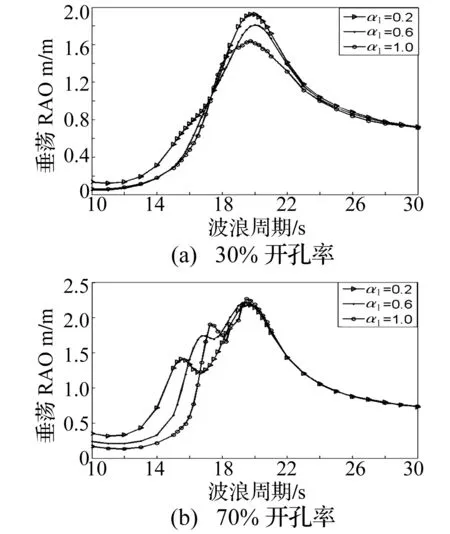
圖8 α1對平臺垂蕩的運動影響分析Fig.8 The analysis of the effect of α1 to the platform heave

圖9 α3對月池內流體的運動影響分析Fig.9 The analysis of the effect of α3to the fluid motion in the moon pool

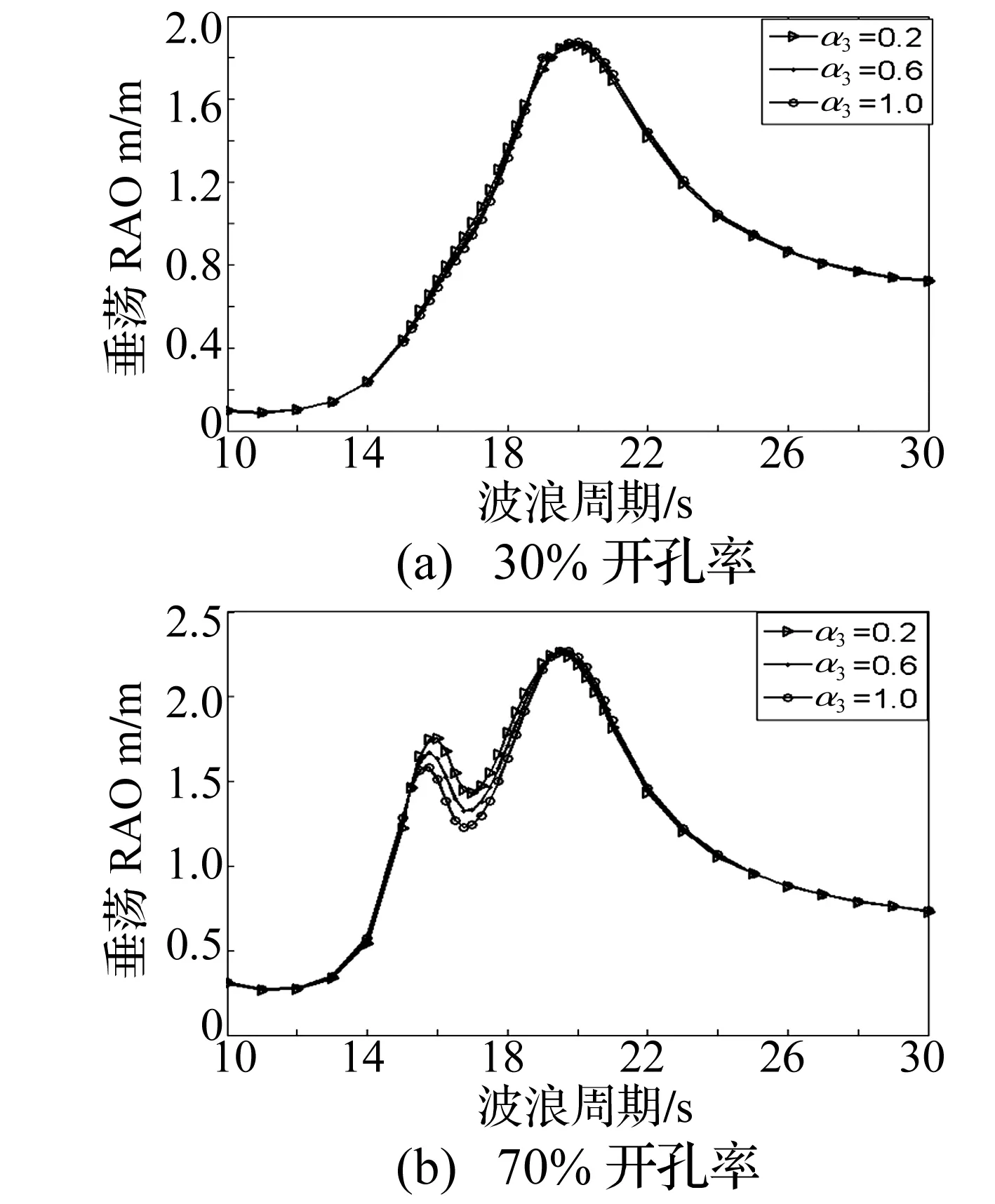
圖10 α3對平臺垂蕩的運動影響分析Fig.10 The analysis of the effect of α3 to the platform heave

圖11 α4對月池內流體的運動影響分析Fig.11 The analysis of the effect of α4to the fluid motion in the moon pool

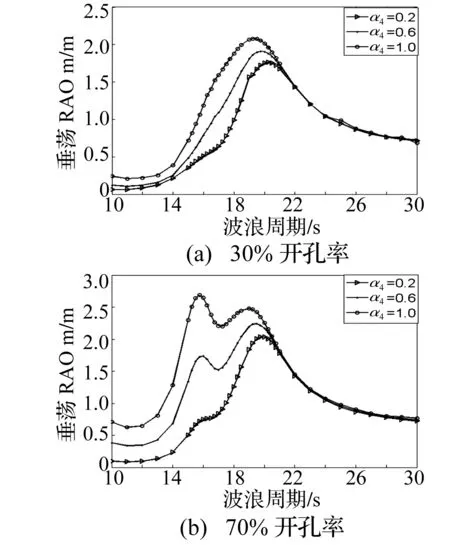
圖12 α4對平臺垂蕩的運動影響分析Fig.12 The analysis of the effect of α4 to the platform heave

圖7和圖8表明，α1顯著影響月池內部流體運動及平臺垂蕩運動。隨著α1的增加，月池內部流體垂向運動的固有周期增加；對于30%的開孔率，平臺的垂蕩運動幅值隨α1的增加而減小；對于70%的開孔率，α1對平臺垂蕩響應RAO曲線的高頻峰值影響較為明顯，增加α1后，高頻峰值增大且固有周期增加。圖9和圖10表明，α3影響月池內部流體垂向運動的幅值，增大α3后月池內流體的垂蕩運動幅值減小；對于平臺的垂蕩運動，70%開孔率時，由于平臺垂蕩與月池內流體垂向運動的耦合較強，α3對平臺垂蕩運動的高頻峰值有一定的影響。圖11和圖12表明，α4對平臺垂蕩運動影響顯著，隨著α4的增加平臺的垂蕩運動幅值增大；對于大的開孔率，平臺垂蕩運動的高頻峰值隨α4的增加逐漸增大，并最終超過低頻峰值，α4對月池內流體的垂向運動幅值也有一定的影響。

4 結 論

本文考慮半開口月池，推導了桁架式Spar平臺垂蕩-縱搖-月池內流體垂向振動的耦合運動方程及月池內流體對平臺垂蕩和縱搖運動產生的力和力矩，計算了耦合系統的運動響應，分析了月池內流體對平臺垂蕩和縱搖運動的影響及耦合參數對平臺及月池內流體運動的影響。結果如下：

(1) 當波浪周期較小時，月池內流體對平臺主體垂蕩有抑制作用，且抑制程度與月池開孔面積有關，在實際中可設計月池底部擋板的最優開孔面積來最大程度地減小平臺主體的垂蕩運動。

(2) 對于70%的開孔率，平臺主體垂蕩RAO有兩個峰值，分別出現在月池流體垂向振動固有周期及平臺主體垂蕩固有周期附近。70%開孔率時，月池內流體的運動幅值大于30%開孔率的情況。考慮月池開口后平臺的縱搖響應變化較小。

(3) 月池附加質量α1顯著影響月池內流體垂向運動的固有周期和響應幅值及平臺垂蕩的響應幅值；平臺對月池的質量耦合系數α3影響月池內部流體垂向運動的幅值，當月池開孔率為70%時，α3對平臺垂蕩運動的高頻峰值有一定的影響；月池對平臺的質量耦合系數α4對平臺垂蕩運動影響顯著，當月池開孔率為70%時，α4對月池內流體的垂向運動幅值也有一定的影響。

[1] 單鵬昊,任慧龍,李輝,等. 極限海況下Spar平臺系泊系統耦合動力分析[J].海洋工程, 2013,31(2): 35-40.

SHAN Penghao, REN Huilong, LI Hui, et al. Coupled dynamic analysis of mooring system of Spar platform under extreme conditions [J]. Ocean Engineering, 2013, 31 (2) : 35-40.

[2] 龍筱曄,李巍,尤云祥.風浪流中Truss Spar平臺耦合動力響應分析[J].中國海洋平臺, 2013, 28(1): 29-35.

LONG Xiaoye, LI Wei, YOU Yunxiang. Analysis of the coupled response of dynamic Truss Spar platform with wind and wave [J]. Offshore Platform, 2013, 31(2):35-40.

[3] KIM M H, RAN Z, ZHENG W. Hull/Mooring coupled dynamic analysis of a truss spar in time domain [J]. International Journal of Offshore and Polar Engineering, 2001, 11(1): 42-54.

[4] GUPTA H, BLEVINS R, BANON H. Effect of moonpool hydrodynamics on spar heave[C]//In: Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering. New York: American Society of Mechanical Engineers, 2008:275-282.

[5] BARREIRA R, SPHAIER S H, MASETTI I Q. Behavior of a mono-column structure(monobr) in waves [C]//In: Proceedings of 24th International Conference on Offshore Mechanics and Arctic Engineering.New York: American Society of Mechanical Engineers, 2005:867-873.

[6] SPHAIER S H, TORRES F G S. Monocolumn behavior in waves: Experimental analysis [J]. Ocean Engineering, 2007, 34(11/12): 1724-1733.[5] ZHOU Huawei, ZHANG Hongsheng. Radiation and diffraction analysis of a cylindrical body with a moon pool[J].Journal of Hydrodynamics,2013,25(2):196-204.

[8] LIU Liqin, INCECIK A, ZHANG Yongheng, et al. Analysis of heave motions of a truss spar platform with semi-closed moon pool [J]. Ocean Engineering, 2014, 94:162-174.

[9] 劉利琴, 張永恒, 滿金雙,等. Spar平臺主體垂蕩-月池流體耦合運動模型試驗研究[J].哈爾濱工程大學學報, 2015, 36(3): 287-291.

LIU Liqin, ZHANG Yongheng, MAN Jinshuang, et al. The research of coupling motion of heave-motion of fluid in the moon pool of body of Spar platform[J]. Journal of Harbin Engineering University, 2015, 36(3): 287-291.

[10] BION S, STEVE L, LEVERETTE S,et al. Motion of a large disconnectable buoy within fpso turret moon-pool [C]//In:Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering. San Francisco: American Society of Mechanical Engineers,2014:24371-24379.

[11] LIU Hengxu, DUAN Wenyang. Introduce dissipation for cylindrical structures with moon-pool of restricted entrances [J].Journal of Harbin Institute of Technology,2015,22:56-60.

[12] 趙晶瑞.經典Spar平臺非線性耦合動力響應分析[D].天津：天津大學, 2010.

[13] FALTINSEN O M, TIMOKHA A. Sloshing [M]. Cambridge University Press, 2009.

[14] WEGGEL D C, ROESSET J M. Vertical hydrodynamic forces on truncated cylinders[C]//In: Proceedings of the 4thInternational Offshore and Polar Engineering Conference. Osaka, Japan, 1994:210-217.

[15] PETTER A B. Dynamic response analysis of a truss spar in waves [D].Newcastle, University of Newcastle, 2000.

Coupling motions among vertical vibration of fluid inside a moonpool and heave-pitch of a spar platform

LIU Liqin, QIU Yu, ZHANG Yongheng, TANG Yougang

(State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

Coupling vibrations among heave-pitch of a truss Spar platform and vertical vibration of fluid inside a moonpool were studied considering semi-opening of the moon-pool. The coupled motion equations for the heave-pitch of the Spar platform and the vertical vibration of fluid inside the moon pool were established, and the forces and moments generated by fluid inside the moon-pool to the heave and pitch of the platform were deduced, respectively. Three cases were considered, they were the 0% opening ratio, the 30% opening ratio and the 70% opening ratio of the moon pool. The motion responses of the coupled system were calculated numerically and the influences of fluid inside the moon-pool on the heave and pitch motions of the platform were analyzed. It was shown that the fluid in the moon-pool reduces the heave motions of the platform, and the level of reduction is related to the opening ratio of the moon-pool; for the 70%opening rate, a smaller peak occurs in the RAO curve of the heave response of the platform nearby the natural vibration period of vertical motion direction of the fluid in the moon-pool; for the opening rate of 70%, the movement of fluid in the moon-pool is much larger than that for the 30% opening ratio; the pitch response of the platform changes slightly when the semi-opening of the moon pool is considered. The effects of coupling parameters on the motions of the platform and the motions of fluid inside the moon pool were analyzed as last.

Spar platform; semi-opening moon pool; heave-pitch coupling; analysis of coupling parameters

國家自然科學基金(51179125)

2015-04-01 修改稿收到日期：2015-09-23

劉利琴 女，博士，副教授，1977年生

P751; TB123

A

10.13465/j.cnki.jvs.2016.19.019