淺析如何以多元智能理論實現小學高段數學應用題高效教學

楊晨

摘 要：多元智能理論是由美國著名心理學家霍華德·加德納（Howard Gardner）率先提出的教學理論，他從多元的角度對人的思維空間進行了重新探索，創造性地提出人至少應該擁有八種智能。如此耳目一新的教學理論，即便是在今天，仍然有著熠熠生輝的教學價值。本文正是以此為源泉，就如何在高段數學應用題的教學中更好地開發學生們的大腦空間，培養他們的發散思維，提高他們解決問題的實際能力，展開了如下探索。

關鍵詞：多元智能理論；小學數學；高段數學應用題教學

一、背景介紹

多元智能理論由美國著名心理發展學家霍華德·加德納（Howard Gardner）提出的，他的這一觀點與單一智能理論截然不同，其強調了每個人至少擁有八種智能且各自在不同領域發揮著超乎他人想象的潛能，包括語言、數理、空間、運動、音樂、人際等。這樣的教學觀點給人耳目一新的感覺，與傳統教學中對學生語言能力和數學邏輯的單一培養有著顯著的區別，為教育教學的改革與實踐指明了新的方向，也提出了新的任務。在多元智能理論的指導下，關于學生們多元智能的培養及個性化能力的挖掘已成為我們教學實踐的焦點。作為新時期的教師，我們從多元智能理論中收獲的不僅是民主平等的師生觀，還有它為我們的教學設計和教學管理帶來的新思路。同時，數學新課標強調了“小學數學教學要結合生活經驗，為學生創造觀察、實踐和探索的機會，從而培養學生的多元智能”。我們在小學高段數學的教學實踐中發現，在多元智能理論的指導下，數學課堂的活躍度和學生學習成果的轉化率確實得到了提升。本文以《列方程解決稍復雜的百分數應用題（1）》的教學設計為例，反思淺析如何以多元智能理論實現小學高段數學應用題的高效教學。

二、教學設計

（一）課前準備

溫故知新，利用上幾課時對百分數的認識與實際運用為新課做鋪墊和知識復習。

1. 計算以下方程式

x+20%x=12 x-15x=17

15x-x=2.8

2. 分組討論說明以下數量關系

（1）公園里的松樹有100棵，櫻花樹比它多30%；

（2）學校里女生比男生少20%；

（3）今年家里日常支出比家庭成員總收入低30%；

（4）小紅比去年長高了10%；

（這道題我們允許學生用語言組織的形式描述以上提及的數量關系，也可以用畫圖、線段圖等方式來體現）

3. 列方程解應用題

A班圖書角的文學讀物比B班少26本，A班讀物是B班的■。A班和B班圖書角的文學讀物各有多少本？

導入階段我們采用循序漸進的方法，逐漸引導學生從簡單的解方程式再到組織學生進行討論，學會用自己的理解與原有知識進行數量關系的說明，最后再讓學生學會用方程進行應用題的解析。在這一階段，學生的反應與討論將他們的知識掌握情況全部暴露出來，也激發了他們后續學習的求知欲。在這個溫故知新的過程中，學生們不僅熱了身練了手，為接下來的新知識的學習做好了準備，而且討論的過程也活躍了課堂氣氛，為接下來的“教”開了個好頭。

（二）課中探究

1. 出示例題1：陽光小學舞蹈組有50人，男生人數是女生人數的50%。舞蹈組里男生、女生分別有多少人？

（1）提問學生：反復讀題，理解題意后根據題目中提到的關系，你能說出其中的數量關系嗎？

（2）給學生討論和解析題目的時間。

（3）引導學生進行畫圖解析。提問學生：畫圖是不是可以更加直觀地體現男、女生之間的數量關系，那么我們首先要畫誰，要怎么畫才能更清楚？

（4）引導學生得出數量關系：男生人數+女生人數=舞蹈組的總人數。

（5）自由討論，讓學生合作列出方程式進行解答。

（6）教師幫助檢驗方程的結果。

（7）討論總結計算方法。

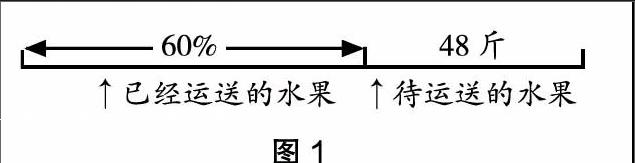
2. 出示例題2：水果批發市場今天要往本地某酒店運送一批水果，目前已經運走了60%，現在還剩48斤待送，請問，這批水果一共有多少斤？

（1）提問學生：反復讀題，理解題意后根據題目中提到的關系，你認為該怎么畫線段圖？（圖1為線段圖模板，學生可以自由發揮）

（2）根據自己畫的線段圖說出數量關系。（這批水果的總數=已經運送的水果+待運送的水果）

（3）根據這個數量關系，是否可以列出方程式進行解答？

（4）以兩人為一搭檔，彼此交換答案進行帶入檢驗。

（5）全班分享解題步驟、思路并自評、互評，選出代表上講臺做公開演示。（全班分為四組，每組派一名代表進行演示，一方面演繹計算過程，讓理解較慢的學生了解步驟，引導學生們在合作匯報的過程中取長補短；另一方面也培養學生公開演講的技能，在表達的過程中增強他們數學學習的自信心）

3. 對比例題1和例題2，由學生說出兩個例題的異同之處，并尋求用方程式解決應用題的思路與方法。

4. 鞏固練習：

活動：乒乓球拍顛球比拼

（1）準備道具：乒乓球拍2個、乒乓球數顆、計時器一個。

（2）活動流程：全班分為兩組，每組選出一名乒乓球手進行顛球比賽，以1分鐘為時限，掉落重新開始仍算數，誰顛球次數最多誰獲勝。（教師將顛球次數分別寫在黑板上并設計評價表，導入競爭機制，提高活動的參與度）

（3）根據比賽結果，提問學生：兩位同學一共顛球50下，其中A同學顛球20下，B同學顛球30下，請根據這些數字出一道含有數量關系的題目并可用方程式解答。

（4）學生打開思路，根據前述題目，紛紛出題。

（三）歸納小結

提問學生：學完本課，你們學到了什么數學知識？掌握了哪些解決問題的辦法？有什么新的啟發？還存在哪些難題？

小結：

知識與技能：學生通過學前導入到課內探究的四個步驟，主動探索出稍復雜的實際問題的解決方法，并且學會了用語言或圖例分析數量關系。

過程與方法：通過對實際問題的探索和趣味活動的實踐，學生學會了用方程解答應用題的方法。

情感態度與價值觀：培養求知的渴望和探索的精神，并在解決問題中增加自信。

三、教學反思與感悟

1. 打破教材局限，多元素達成激趣

用方程式解應用題對于小學六年級的學生而言稍有難度，如果一味地習題堆砌，很容易導致學生產生疲憊，甚至厭學。因此在教授這堂課時，根據多元智能理論，教師要打破教材局限，優化教材的兩個問題，首先在習題的內容上下功夫，不僅要與學生生活緊密相關，譬如我們前文涉及的圖書角話題等，還要延伸習題涉獵的范疇，在提升學生數理邏輯智能的同時開發他們的語言表達、視覺空間和運動等智能；其次要因材施教，給不同學生施展的機會，即使他們對教材內容的掌握較為吃力，也不可埋怨批評，而應該尋找他們的興趣點分別輔導，進而激發每個學生的學習熱情。在日后的課堂教學中，教師還得在“趣”上面多下功夫，將教材與學生的生活實際相結合，以生活中原汁原味的“趣”激發學生們的多元智能。

2. 打破思維束縛，分途徑實現解析

解答應用題本身就是培養數理邏輯智能的方式，同時它也是數學課主要的智能培養方向，學生要學會發現問題并建立數學模型，展開解析，但一個班級里學生的性格與智能偏向是非常復雜的，為了創造一個開放的課堂，教師應該打破思想束縛，允許學生利用特長解決問題。譬如，語言智能優秀的學生擅長描述數量關系，可以幫助其他學生理清思路，或者在上述算式演算環節中獨挑演講的大梁；運動智能較強的學生擅長畫圖或動手實驗，如乒乓球打得好的，還可以在鞏固練習中“練一手”；還有一部分學生則擅長與他人合作，通過溝通與交流，取長補短，尋求幫助，進而找到解決問題的辦法……學生的潛能是非常巨大的，教師開放思想，他們就能開放想象，即便再煩冗復雜的課題也能分工、分途徑完成與實現。

總之，多元智能理論與我們數學教學中培養學生的發散思維不謀而合，對于創造更具開放性、創造性與生命力的數學課堂，有著顯而易見的推動作用。在教的過程中，我們要善于將理論聯系實際，根據自身數學教學的實際情況發現學生的閃光點，有意識地培養學生多元的思維能力，促進他們的個性成長，同時，在多元化的教學活動中，還要讓學生獲得更多動手實踐的機會，彰顯數學課程的應用性特征，促進數學教學的知行合一，在教會學生們“思”的同時，教會他們如何“做”。