隨機截尾數據下的液壓泵故障分布的兩參數威布爾分布模型*

熊申輝，胡良謀，胡　飛，曹克強，景　濤，高　斌

(1. 空軍后勤部 司令部，北京　100720；2. 空軍工程大學 航空航天工程學院，西安　710038；3. 廣州軍區 空軍裝備部，廣州　510071)

?

隨機截尾數據下的液壓泵故障分布的兩參數威布爾分布模型*

熊申輝1，胡良謀2，胡飛3，曹克強2，景濤2，高斌2

(1. 空軍后勤部 司令部，北京100720；2. 空軍工程大學 航空航天工程學院，西安710038；3. 廣州軍區 空軍裝備部，廣州510071)

液壓泵在使用階段的可靠性能最真實地反映產品的實際可靠性水平和薄弱環節，其可靠性數據具有隨機截尾特性，因此其可靠性數據分析面臨著諸多困難。首先提出了一種基于隨機截尾數據的兩參數威布爾分布的建模方法，并將其應用于某型液壓泵的可靠性數據分析，最后進行了仿真試驗研究。仿真試驗結果表明，基于平均秩次法的液壓泵兩參數威布爾分布模型比基于殘存比率法的兩參數威布爾分布模型更為精確，同時驗證了威布爾分布的優越性。研究成果為基于隨機截尾數據的液壓泵提供了一種更為精確的可靠性分析方法。

液壓泵；隨機截尾數據；兩參數威布爾分布；平均秩次法；殘存比率法

0　引言

液壓泵[1-3]是飛機液壓傳動與控制系統中的能源部件，它的作用是向系統提供一定壓力和流量的油液。從能量轉換的觀點來說，液壓泵是把機械能轉換為液壓能的裝置。為了指導使用維護工作，迫切需要進行液壓泵的可靠性分析。

液壓泵在使用階段的可靠性數據分析具有重要的研究意義。這是因為液壓泵在使用階段反映的使用及環境條件最真實，參與評估的液壓泵數量較多，因此在該階段收集的可靠性數據極為珍貴，它能最真實地反映液壓泵的實際可靠性水平和薄弱環節，對設計和制造的評價最權威，其可靠性數據分析結果是可靠性工作的最終檢驗，也是今后開展新型液壓泵可靠性設計的最有價值的參考。

在實際工作中，同類型的液壓泵投入使用的時間不同；觀測者記錄數據時除故障時間外，還有一些液壓泵統計時仍在完好地工作；以及使用中途液壓泵會因某種原因轉移他處等，這些原因都導致了液壓泵在使用階段收集的可靠性數據具有隨機截尾的特性。隨機截尾型可靠性數據由于其獨特的數據特征，其可靠性分析面臨著諸多困難和難點，相關技術的研究與開發一直都是可靠性工程領域的研究熱點和難點。

威布爾分布[4-5]是一種連續分布，它能夠描述航空產品各種類型失效數據的分布規律，其優點在于它對各種類型的試驗數據具有極強的適應能力，能夠充分地描述失效機理。因此在可靠性分析方面，威布爾分布成為近年來研究最為廣泛的參數模型。

本文主要研究隨機截尾數據下的兩參數威布爾分布的建模方法，并將其應用于某型液壓泵的可靠性數據分析。

1　兩參數威布爾分布模型

兩參數威布爾分布的分布函數為[5-10]

(1)

式中：η稱為尺度參數，m稱為形狀參數。

2　隨機截尾數據下的兩參數威布爾分布模型

兩參數威布爾分布的未知參數包括尺度參數和形狀參數。只有在確定這兩個參數后，才能利用分布模型計算各個可靠性指標。

2.1隨機截尾數據下的經驗分布函數計算

隨機截尾數據下，經驗分布函數的計算有兩種方法，分別為殘存比率法和平均秩次法[6-7]。

2.1.1殘存比率法

殘存比率法為通用公式，在無刪除樣品時同樣適用。殘存比率法是由概率乘法公式得到的，因此它適用于樣本量較大的情況。

產品在某時刻ti的可靠度為：

R(ti)=R(ti-1)·S(ti)

(2)

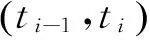
(3)

式中：ξ是指產品從處于完好狀態開始直到進入失效狀態所經歷的時間，也可稱之為壽命，是一非負隨機變量。

根據樣本觀測值進行估計，其計算公式為：

(4)

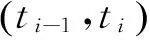
(5)

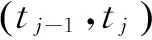
根據式(2)，經驗分布函數的計算公式為：

(6)

2.1.2平均秩次法

平均秩次法是一種在隨機截尾數據下經驗分布函數的較精確的計算方法，其思想為：對于一組隨機截尾的樣本數據，可按其失效時間和刪失時間的大小排列成一組順序統計量，其中每一個樣品的失效時間都有一個順序號，此順序稱為秩次。而對于那些尚未失效而中途撤離的樣品，什么時間失效無法預計，然而可以估計出它們所有可能的秩次，再求出平均秩次，將平均秩次代入近似中位秩公式，即可求出其經驗分布函數。

對于隨機截尾數據，統計學家們給出一個計算平均秩次的增量公式，為：

(7)

(8)

式中：Ak為失效樣品的平均秩次，下標k代表失效樣品的順序號；Ak-1為前一個失效樣品的平均秩次；i為所有產品的排列順序號，按故障時間和刪除時間的大小排列。

然后將平均秩次代入近似中位秩公式計算樣本的經驗分布函數，為：

(9)

2.2隨機截尾數據下的兩參數威布爾分布的最小

二乘估計法

對于隨機截尾數據，假設失效樣品的數量為n1，刪除樣品的數量為n2，則n1+n2=n。假設失效樣品的失效時間的順序統計量為t1≤t2≤…≤tn1，根據殘存比率法或平均秩次法可計算其經驗分布函數為Fn(tk)(k=1,2,…,n1)。

式(1)可以表示為線性方程形式，為：

(10)

因此可以根據最小二乘法來估計隨機截尾數據下的兩參數威布爾分布。

令

(11)

需擬合的回歸直線方程為：

y=a+bx

(12)

根據最小二乘法原理，回歸系數和相關系數為：

(13)

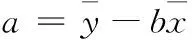
(14)

(15)

式中：

2.3兩參數威布爾分布參數的求解

根據回歸系數a、b，威布爾分布的參數為：

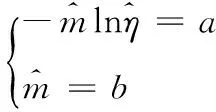
(16)

2.4線性相關程度檢查

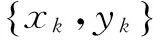
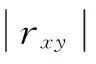
3隨機截尾數據下的液壓泵的兩參數威布爾

分布建模流程

基于兩參數威布爾分布的隨機截尾數據下的液壓泵可靠性數據分析的一般流程如圖1所示。

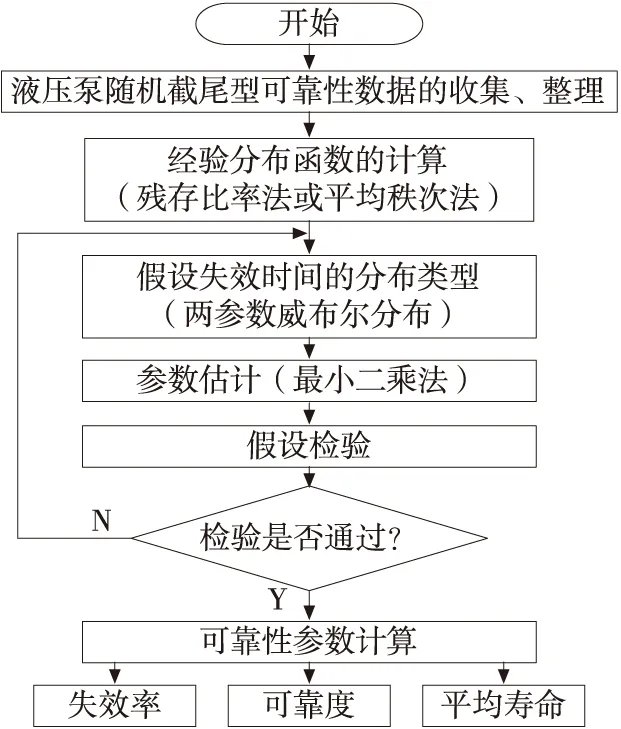
圖1　基于兩參數威布爾分布的隨機截尾數據下

首先收集液壓泵的隨機截尾型可靠性數據，然后根據殘存比率法或平均秩次法計算樣本的經驗分布函數。假設服從兩參數威布爾分布，根據數理統計的基本原理，對液壓泵的可靠性數據進行參數估計，并使用假設檢驗方法來驗證壽命分布類型，最后再進行液壓泵可靠性參數的計算。

4　液壓泵的可靠性分析仿真試驗

4.1仿真數據

4.2經驗分布函數的計算

采用殘存比率法計算失效樣品的殘存概率S(ti)及經驗分布函數Fn(ti)的計算結果如表1所示；采用平均秩次法計算失效樣品的平均秩次Ak及經驗分布函數Fn(ti)的計算結果如表1所示。

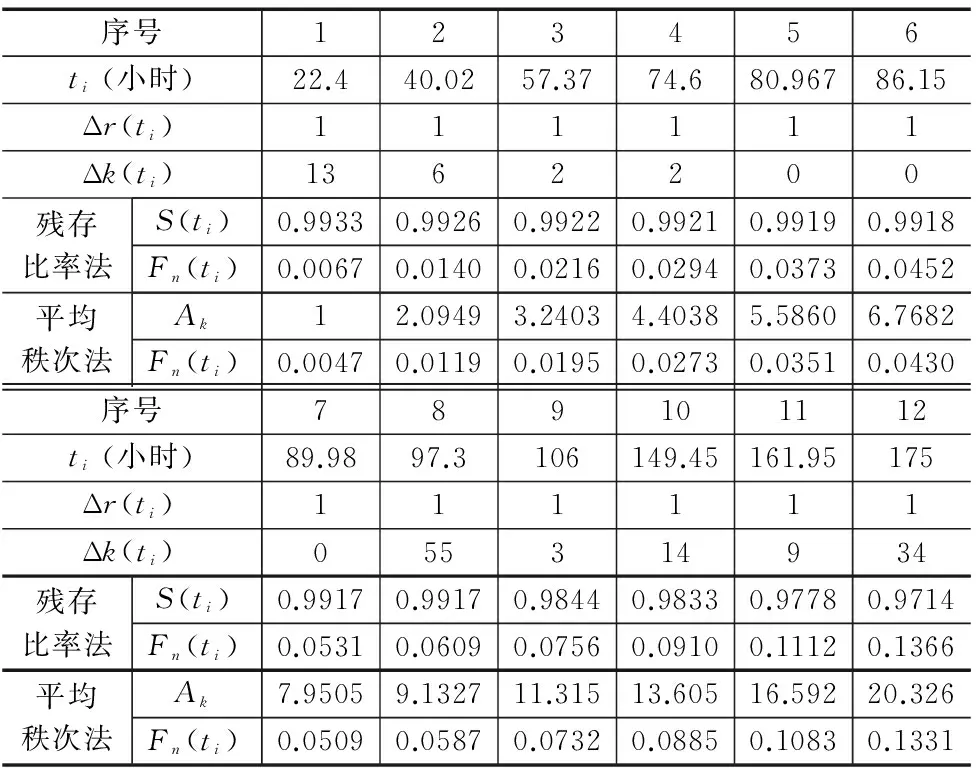
表1　液壓泵的外場使用故障數據及平均秩次、

4.3兩參數威布爾分布模型的建立

(1)基于殘存比率法的兩參數威布爾分布模型

在殘存比率法計算經驗分布函數的基礎上，兩參數威布爾分布的參數估計(最小二乘法)結果為：尺度參數η1=650.43，形狀參數m1=1.52，相關系數rxy1=0.98998。當顯著水平為0.01時，相關系數臨界值為rα=0.6614，由于rxy1>rα時，則認為回歸效果顯著。

(2)基于平均秩次法的兩參數威布爾分布模型

在平均秩次法計算經驗分布函數的基礎上，兩參數威布爾分布的參數估計(最小二乘法)結果為：尺度參數η2=571.61，形狀參數m2=1.6651，相關系數rxy2=0.99207。當顯著水平為0.01時，由于rxy2>rα時，則認為回歸效果顯著。

(3)小結

由于rxy 1< rxy 2，因此基于平均秩次法的液壓泵兩參數威布爾分布模型比基于殘存比率法的兩參數威布爾分布模型更為精確。因此對于隨機截尾數據，平均秩次法比殘存比率法的建模效果更好。

基于平均秩次法的兩參數威布爾分布模型的概率圖如圖2所示。從圖2可以看出，數據點大體上是沿一條直線分布的，這直觀地說明了該型液壓泵的首次失效時間可以用兩參數威布爾分布來建模。

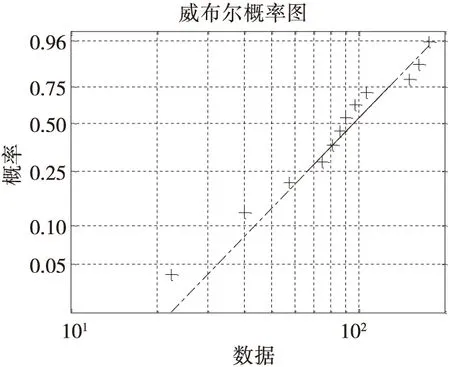
圖2　兩參數威布爾分布的概率圖

4.4基于平均秩次法的液壓泵可靠性參數的計算

液壓泵首次失效時間的基于平均秩次法的兩參數威布爾分布的分布函數為：

分布密度函數為：

失效率函數為：

失效率曲線如圖3所示，可以看出，失效率隨時間增長呈增長特性，因此液壓泵的失效類型為耗損失效，故障原因主要是由于老化、疲勞和耗損引起的。因此通過可靠性定量分析，就可以采取預防維修或更新措施，更換某些元器件，把液壓泵上升的失效率降下來。

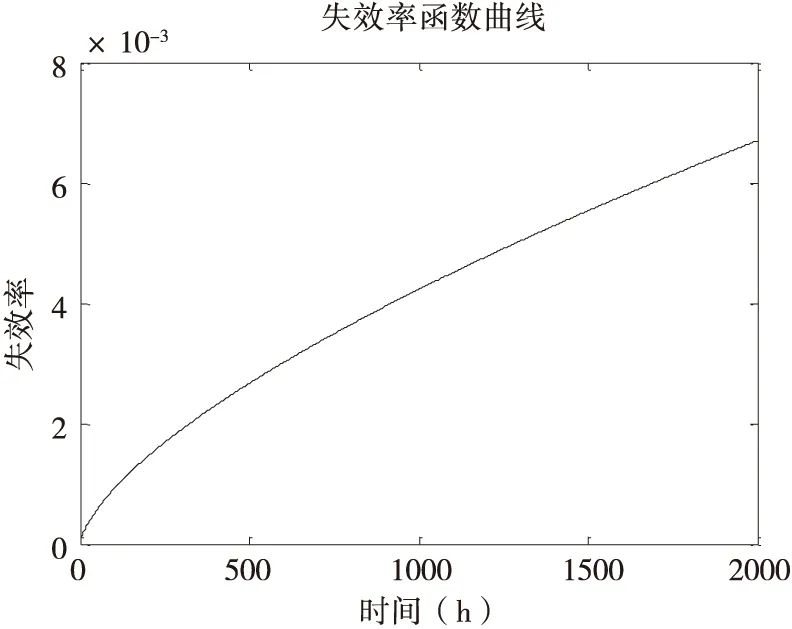
圖3　液壓泵的失效率曲線

可靠度函數為：

平均壽命為：

θ=ηΓ(1+1/m)=510.78(h)

5　結論

由于兩參數威布爾分布擬合能力強、適用范圍廣，是可靠性工程中常用的分布之一，對其進行精確的參數估計在可靠性分析中有相當重要的意義。

本文首先提出了一種基于隨機截尾數據的兩參數威布爾分布的建模方法，并將其應用于某型液壓泵的可靠性數據分析，最后進行了仿真試驗研究。仿真試驗結果表明：①平均秩次法原理清晰，計算過程方便快捷，同時還具有計算機編程方便、擬合精度高等優點，基于平均秩次法的液壓泵兩參數威布爾分布模型比基于殘存比率法的兩參數威布爾分布模型更為精確；②兩參數威布爾分布擬合能力強，驗證了威布爾分布的優越性。研究成果為基于隨機截尾數據的液壓泵提供了一種更為精確的可靠性分析方法。

[1] 胡良謀，曹克強，任博，等. 飛機液壓系統使用故障統計分析[M]. 北京：國防工業出版社，2014.

[2] 王占林. 飛機高壓液壓能源系統[M]. 北京：北京航空航天大學出版社，2004.

[3] 梁廣輝，薛俊杰，胡良謀，等. 基于非對稱貼近度的飛機液壓系統使用工況模糊綜合評判[J]. 組合機床與自動化加工技術，2014(4)：83-86.

[4] Weibull W. A statistical distribution function of wide applicability[J]. Journal of Applied Mechanics, 1951, 18 (3): 293-297.

[5] 凌丹. 威布爾分布模型及其在機械可靠性中的應用研究[D].成都：電子科技大學，2010.

[6] 賀國芳. 可靠性數據的收集與分析[M]. 北京：國防工業出版社，1995.

[7] 趙宇，楊軍，馬小兵. 可靠性數據分析教程[M]. 北京：北京航空航天大學出版社，2009.

[8] 范晉偉，梁曉霞，鄭德榮，等. 基于灰關聯度的數控磨床故障間隔時間分布模型決策[J]. 組合機床與自動化加工技術，2014(8)：78-81.

[9] 孟慶東，楊珍.基于MCMC的MTBF值區間估計方法研究[J]. 組合機床與自動化加工技術，2013(2)：67-69.

[10] 董慧敏，劉勇軍，張新鋒. 鎂錠切削機故障分布擬合與MTBF評估研究[J]. 組合機床與自動化加工技術，2014(1)：107-113.

(編輯趙蓉)

Two Parameter Weibull Distribution Model of Fault Distribution for Hydraulic Pump Based on Random Censored Data

XIONG Shen-hui1, HU Liang-mou2, HU Fei3, CAO Ke-qiang2, JING Tao2, GAO Bin2

(1. Command Ministry of Air Force Logistics Ministry, Beijing 100720, China;2. College of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi′an 710038，China)

Operational reliability of hydraulic pump can factually reflect the actual reliability level and weak part. The operational reliability data of hydraulic pump has characteristic of random censored, therefore its operational reliability analysis is very difficult. A modeling method of two parameter Weibull distribution based on random censored data is presented. And then the method is used to establish the two parameter Weibull distribution model of one hydraulic pump. The simulation test is carried out finally. The simulation test results show that the two parameter Weibull distribution model of hydraulic pump based on the mean rank order method is more accurate than the two parameter Weibull distribution model based on the survival ratio method. And the simulation test results show that the Weibull distribution is good. The research work can provide a more accurate method of reliability analysis for hydraulic pump based on random censored data.

hydraulic pump; random censored data; two parameter weibull distribution; mean rank order method; survival ratio method

1001-2265(2016)04-0109-04DOI:10.13462/j.cnki.mmtamt.2016.04.029

2015-06-02；

2015-07-07

中國博士后科學基金特別資助項目(201003788)

熊申輝(1977—)，男，安徽桐城人，空軍后勤部工程師，碩士，研究方向為飛機系統可靠性，(E-mail)xiongsh_2015@163.com。

TH137;TG506

A