基于UG和ADAMS的弧齒圓柱齒輪動力學分析*

賀林莉，侯　力，李　波，魏永峭，張海燕，牟如強

(四川大學 制造科學與工程學院，成都　610065)

?

基于UG和ADAMS的弧齒圓柱齒輪動力學分析*

賀林莉，侯力，李波，魏永峭，張海燕，牟如強

(四川大學 制造科學與工程學院，成都610065)

根據弧齒圓柱齒輪加工原理及其齒面方程，利用UG/Open Grip二次開發語言在UG中完成齒輪的參數化建模，并實現齒輪副的裝配。應用ADAMS對齒輪副進行動力學仿真，得到其在傳動過程中部分參數特性曲線并對其進行分析。鑒于目前關于弧齒圓柱齒輪的研究沒有成熟的動力學分析成果及計算理論，故將分析結果與同樣參數的直齒、斜齒圓柱齒輪的理論計算值進行對比。結果表明：三者周向力、徑向力及法向力比較接近，弧齒輪副的軸向力呈對稱分布，雖然瞬時值較大但其平均值接近于零。研究結果為弧齒圓柱齒輪的動態特性研究和參數優化提供了技術支撐和理論指導。

弧齒圓柱齒輪；UG/Open Grip；參數化建模；動力學

0　引言

隨著現代科學技術及工業的迅速發展，齒輪的常規要求已經不能滿足現階段的應用需求，高精度、高效率、低噪聲、小型化等成為熱門的發展方向。弧齒圓柱齒輪作為一種新型齒輪結構，其齒線是一段圓弧且關于中間截面對稱，能夠承受更大的載荷，有更好的傳動平穩性以及更低的傳動噪聲[1]。

弧齒圓柱齒輪的研究雖然時日較短，但自日本學者長谷川吉三郎提出弧齒圓柱齒輪的概念以來，國內外許多學者一直在對其展開深入研究[2]。九州大學的石橋彰論述了刀盤粗銑-碗型砂輪磨削加工圓弧齒輪的方法[3]。祝海林等人對弧齒圓柱齒輪副的嚙合問題展開了研究工作，由此得到了其根切的界限模型[4]。臺灣的曾睿堂團隊對弧齒圓柱齒輪的數學模型和接觸特性做了深入推導和研究[5-6]。哈爾濱工業大學的陳明教授團隊對弧齒圓柱齒輪副的嚙合性能展開了大量的研究，討論了干涉、軸線平行誤差以及中心距的影響，并將變位引入弧齒圓柱齒輪中[7]。馬振群等人研制出了能夠在數控機床上實現齒面完全修形的方法[8]。宋愛平等人提出了運用銑削的方式加工圓弧齒線圓柱齒輪，并發明了一種運用這種加工方式的“平行連桿式”的加工工具[9]。王少江等人對面向制造的弧齒圓柱齒輪的成型機理及強度分析進行了較為深入的研究[10]。

綜上所述，弧齒圓柱齒輪傳動是一個亟待開發且大有前景的領域，但現階段的研究主要是針對弧齒圓柱齒輪的加工方法和靜力學分析，對該齒輪的動力學分析和相關理論的研究基本處于空白，因此對其進行動力學分析是非常有必要的。

1　弧齒圓柱齒輪模型創建

現階段弧齒圓柱齒輪比較被認可的加工方法是用處在同一圓周上的刀具進行切削加工，其成形原理如圖1所示。

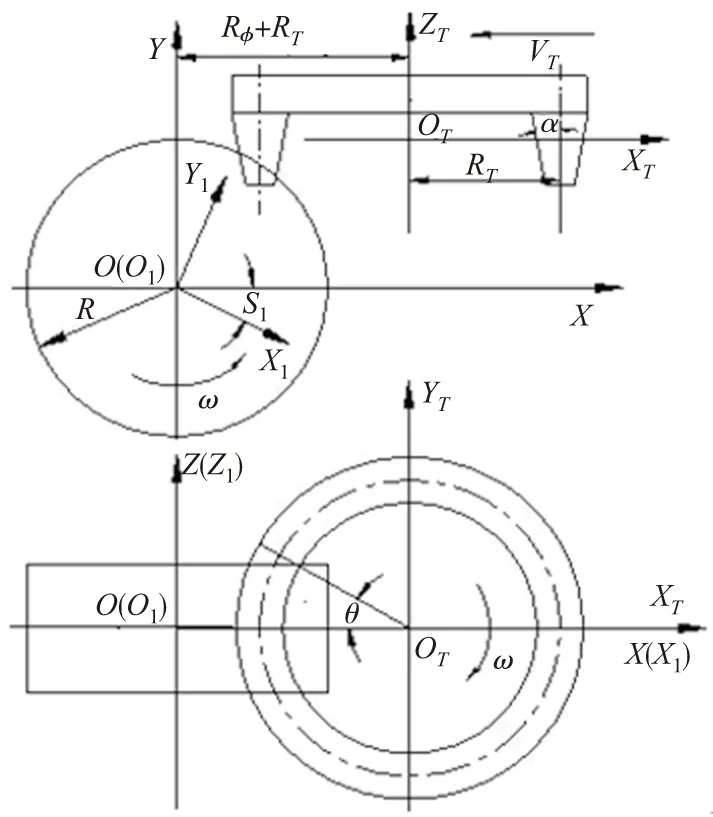
圖1　弧齒圓柱齒輪成形原理

根據上圖圓弧齒線圓柱齒輪的加工原理，可推導出其齒面方程如下[10]：

(1)

根據齒面方程并參考直齒圓柱齒輪的創建方法，本文采用基本圓弧齒條作為刀具，模擬弧齒圓柱齒輪與圓弧齒條的嚙合過程，切制弧齒圓柱齒輪[11]。而實現上述操作，只需在UG/Open Grip環境之下編程實現齒坯與圓弧齒線齒條的嚙合滾切運動。實際應用時，只需調用程序，輸入模數m、齒數z、齒寬b、刀盤直徑dp(齒線直徑)等參數，UG即可自動切制出所需參數的弧齒圓柱齒輪，實現其參數化建模。如圖2所示為模數m=4、齒數z=36、齒寬b=46、刀盤直徑dp=127的弧齒圓柱齒輪切制過程。

圖2　齒輪的切制過程

2　弧齒圓柱齒輪動力學分析

2.1理論基礎

ADAMS是一款機械系統動力學分析軟件，主要研究的是多體系統動力學特性和運動規律，在齒輪系統分析中有著重要意義[12]。在動力學分析過程，由于齒輪副的嚙合存在著相互接觸碰撞，不可避免的會產生接觸力，這個接觸力也就是通常所講的齒輪嚙合力。在ADAMS中有兩種計算接觸力的方法：一種是補償法(Restitution)；另一種是沖擊函數法(Impact)。補償法需要確定兩個參數：懲罰系數(Penalty)和補償系數(Restitution)。沖擊函數法是根據Impact函數來計算兩個構件之間的接觸力，接觸力由兩個部分組成：一個是由于兩個構件之間的相互切入而產生的彈性力；另一個是由相對速度產生的阻尼比。本文選擇沖擊函數法為計算方式。

2.2模型導入

圖3　齒輪副模型圖

ADMAS與UG之間有可靠的數據共享、交換接口，本文利用UG建立齒輪三維模型并實現齒輪副的虛擬樣機裝配。然后將其格式轉換為x_t模式，進而在ADAMS中選擇導入命令。如圖3所示為模數m=4，齒數分別為z1=25，z2=36，齒寬b=46mm，齒線半徑R=63.5mm的弧齒圓柱齒輪傳動副模型。

2.3參數設定

ADMAS動力學仿真參數包括工作環境、結構材料、接觸參數等項目。工作環境主要包括柵格大小(選擇“編輯-柵格”設置柵格大小為10mm×10mm)、單位(通過“編輯-設置-單位”，選擇單位制為毫米·千克·秒，mm·kg·s)；設置齒輪副的材料為結構鋼；剛度系數為8.144E+005N/mm1/2。同時對該齒輪副的運動形式加以確定，對其施加符合實際情況的約束。在齒輪系統運動過程中，齒輪主要繞著其支撐軸做周向旋轉運動，所以在此我們對兩個齒輪添加轉動副(Revolute)。具體操作為選擇轉動副選項，接著選擇“2體1點”選項，然后點擊齒輪和大地，最后點擊齒輪中心點(線)。同時查閱相關資料，確定接觸力的相關計算參數，具體取值如圖4所示。

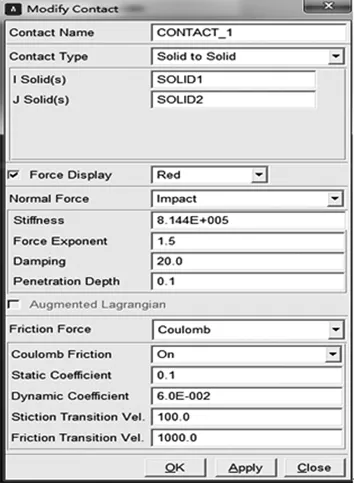
圖4　接觸力相關參數設置對話框

在仿真計算前確定該齒輪副的負載施加如下：在主動輪(小齒輪)上加載恒定的轉速；對從動輪(大齒輪)添加一個恒定為負的負載，其值為300N·m。為了防止突然施加的較大轉速使輪齒受到過大沖擊，速度采用STEP函數進行添加，使轉速在0.02s內由0逐漸增大到600r/min(3600°/s)，如圖5所示。同時選擇分析類型為動力學，仿真時長設置為0.1s，步長為1000，而諸如積分器等參數選擇默認。

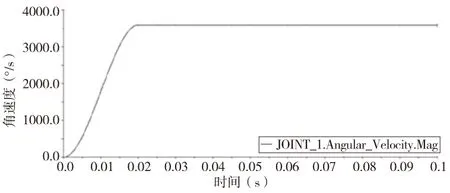
圖5　主動輪轉速曲線

2.4仿真結果與分析

經過動態仿真運算后，得到了該齒輪副的動態特性曲線，主要包括從動輪轉速、周向力、徑向力、法向力以及軸向力。由于初始嚙合時，傳動不平穩狀態較為明顯，故我們主要選擇0.05s～0.1s之間穩定傳動后的狀態進行分析討論。仿真結果如圖6、圖7所示。

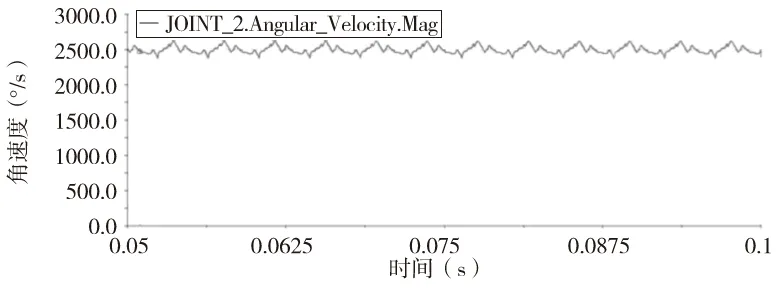
圖6　從動輪角速度

從圖6可以看出弧齒輪副從動輪的角速度在2500°/s上下起伏波動，極值分別為2590.18°/s和2448.29°/s，平均值為2499.35°/s。同時根據傳動比36/25可以得到從動輪的理論角速度為2500°/s，仿真值與其非常接近。所以該齒輪副能夠實現正確的傳動關系。

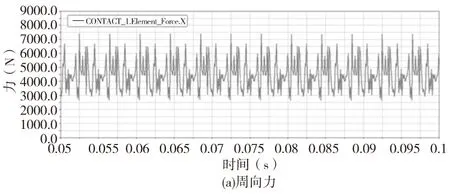
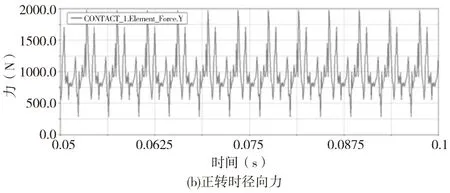
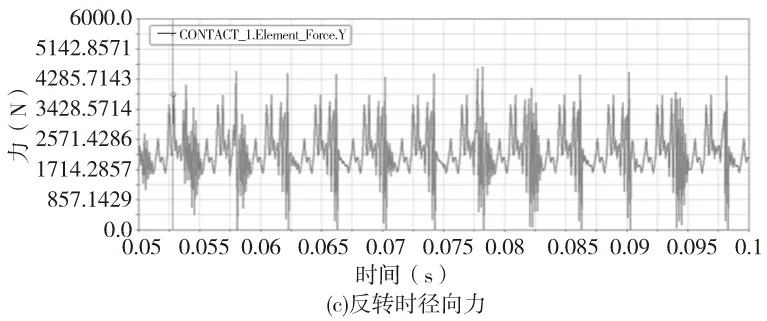
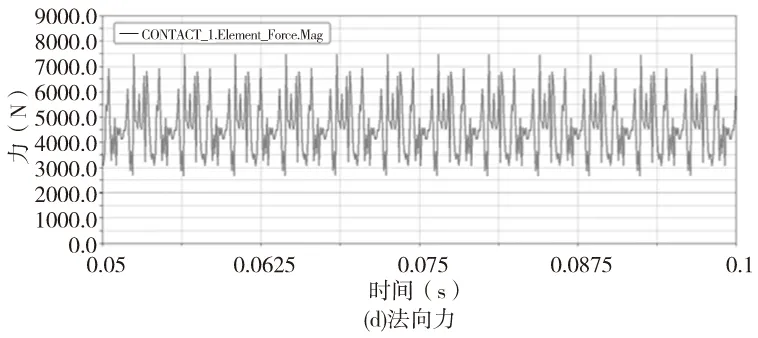
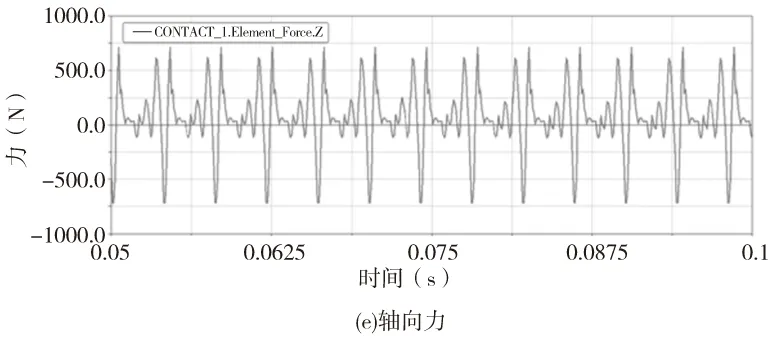
圖7　弧齒輪副嚙合時參數示意圖

由圖7a可知，周向力的極值分別為7397.92N和2681.22N，均值是4180.79N。圖7b、7c分別為該齒輪副正反轉時徑向力在坐標系X軸上的投影值，齒輪副中心線未與仿真環境中的X軸重合，圖7b中的平均值為998.90N而圖7c中為2197.91N，所以得到該齒輪副的徑向力的平均值為1598.41N。圖7d是該齒輪副的法向力分布圖，其值在4515.90N上下成周期性變化。圖7e是軸向力分布圖，從中可以看出其值在0N上下呈周期性波動，且其最值分別為-716.87N和715.22N，可見該齒輪副的軸向力基本呈對稱分布，其均值為22.24N，雖然與理論上的軸向力完全抵消有所出入，但其只占整個嚙合力(法向力)的0.5%左右，在應用上是可以接受的。

鑒于目前關于弧齒圓柱齒輪動力學分析還沒有成熟的方法與分析成果，同時也沒用完善的計算理論。因此上述仿真結果無法得到準確的驗證。而直齒、斜齒圓柱齒輪已建立了成熟的理論體系，因此可以設定模數m=4，齒數分別為z1=25，z2=36，齒寬b=46mm的直齒、斜齒圓柱齒輪傳動副，結合其理論計算值以及齒輪的實際應用情況，驗證前文仿真參數及仿真結果的有效性。根據高等教育出版社的第四版《機械設計》，得到直齒、斜齒圓柱齒輪傳動的載荷計算公式分別如式(2)、式(3)所示。根據公式計算出直齒、斜齒傳動的載荷后與弧齒仿真值進行對比分析。

(2)

式(2)中d1是從動輪分度圓直徑；α是分度圓壓力角，取20°；T是從動輪的轉矩。

(3)

式(3)中d1是從動輪分度圓直徑；αn是法向壓力角，取20°；β是螺旋角，取10°；T是從動輪的轉矩。

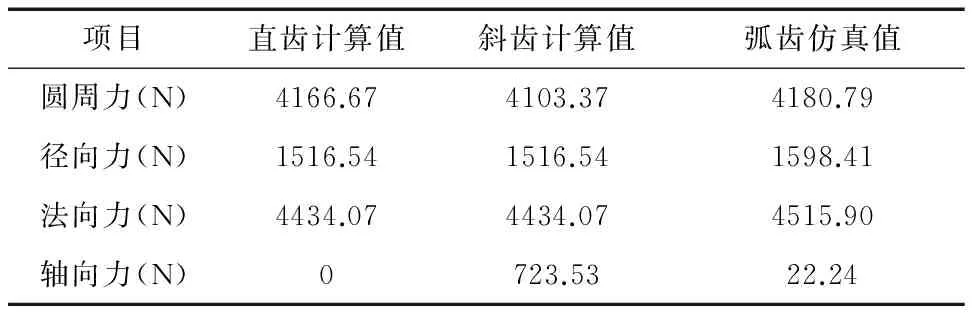
表1　三類圓柱齒輪參數對比表

從表1的結果能夠得出，在決定齒輪形狀的主要參數保持一致的情況下，三種類型的齒輪在其傳動過程中所受到的周向力、徑向力以及法向力相差不大，這與齒輪的實際應用相符，從側面驗證了前文動力學仿真方法和相關參數設定的可行性和有效性。而三種齒輪的軸向力區別較大，直齒輪理論上無軸向力；斜齒輪的理論計算值為723.53N，在三類齒輪中軸向力最大；由于弧齒輪的齒線結構關于中間截面對稱，理論上其軸向力對稱分布且能相互抵消。根據仿真結果來看，其軸向力分布近似于對稱，且兩端最大值幾乎相等，約為716N且其均值為22.24N。即弧齒的軸向力遠小于斜齒，而比直齒的軸向力略大，因此實際應用時應當選用能夠承受一定軸向力的軸承與弧齒輪進行配合使用。

3　結論

(1)分析現有的弧齒成形方法，根據其加工原理及齒面方程，基于UG的二次開發語言實現該齒輪在UG中的參數化建模，極大地提高了建模效率與準確度，為后續的動力學分析奠定了基礎。

(2)對比圓弧齒輪傳動仿真結果與直齒、斜齒輪的理論計算值，并結合實際應用情況進行分析。驗證了本文動力學仿真方法的有效性以及相關約束、工作環境等參數設置的準確性。為弧齒圓柱齒輪動力學仿真提供了參考和依據。

(3)在決定齒輪形狀的主要參數保持一致的情況下，直齒、斜齒、弧齒圓柱齒輪傳動的周向力、徑向力以及法向力相差不大。而圓弧齒輪的軸向力呈現對稱分布，且其平均值接近于零，雖然與理論上的軸向力完全抵消有所出入，總體來說可以接受。但其軸向力瞬時值較大，極值達到716N左右，所以在實際應用時應當選用能夠承受一定軸向力的軸承與弧齒圓柱齒輪進行配對使用。

[1] 常青林,侯力,孫志軍,等.弧齒圓柱齒輪兩種加工方法工藝分析[J].機械傳動,2014,38(6):96-100.

[2] 鄒旻,祝海林.新型圓弧齒線圓柱齒輪[J].制造技術與機床,1995(5):43- 47.

[3] 石橋彰.關于圓弧齒輪的特性[A].日本機械學會論文集[C],日本機械學會,1965,31(225):864-869.

[4] 祝海林,鄒旻,胡愛萍.圓弧齒線圓柱齒輪嚙合理論的研究[J].機械,1996,23(5):7-10.

[5] Rui-Tang Tseng, Chung-Biau Tsay. Contact characteristics of cylindrical gears with curvilinear shaped teeth[J]. Mechanism and Machine Theory,2004,39:905-919.

[6] Rui-Tang Tseng, Chung-Biau Tsay. Mathematical model and undercutting of cylindrical gears with curvilinear shaped teeth[J]. Mechanism and Machine Theory,2001,36:1189-1202.

[7] 狄玉濤,洪曉暉,陳明.弧齒線圓柱齒輪齒面形成原理[J].哈爾濱軸承, 2006, 27(3):58-61.

[8] 馬振群,鄧承毅.弧齒線圓柱齒輪全修形齒面的CNC修形加工方法[J].機械工程學報,2012,48(5):165-171.

[9] 宋愛平,吳偉偉,高尚,等.弧齒圓柱齒輪理想幾何參數及其加工方法[J].上海交通大學學報,2010,44(12):1735- 1740.

[10] 王少江,侯力,董璐,等.面向制造的弧齒圓柱齒輪建模及強度分析[J].四川大學學報:工程科學版,2012,44(2):210-215.

[11] 姜平,侯力,任文娟,等.曲線齒輪的成型原理及嚙合特性分析[J].機械設計與制造,2012(7):197-199.

[12] 趙俊奇.雙圓弧行星齒輪減速器的動力學性能分析[D].大連:大連交通大學,2014.

(編輯趙蓉)

Dynamic Analysis of Cylindrical Gear with Curvilinear Shape Teeth Based on UG and ADAMS

HE Lin-li, HOU-Li, LI Bo,WEI Yong-qiao,ZHANG Hai-yan, MOU Ru-qiang

(College of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065,China)

Based on the processing principle of cylindrical gear with curvilinear shape teeth and the tooth surface equation, the parametric modeling of gear is completed with the secondary development language of UG/Open Grip and the gear pair is assembled in the UG. Using the ADAMS for dynamic analysis of the gear pair, the parameters characteristic curve of gear pair in the process of transmission is got and analyzed. Since there isn’t mature theory of dynamic analysis and computational formula about cylindrical gear with curvilinear shape teeth in the current study, the analysis results of cylindrical gear with curvilinear shape teeth are compared with the theoretical calculation values of spur gear and helical cylindrical gear with the same parameters in this paper. The results showed that the circumferential force, radial force and axial force of spur gear, helical cylindrical gear and cylindrical gear with curvilinear shape teeth are almost the same. The axial force of the gear with curvilinear shape teeth is symmetrical distribution. Although the instantaneous value is larger, its average value is close to zero. The results of the study can provide technical support and theoretical guidance for dynamics research and parameter optimization of the cylindrical gear with curvilinear shape teeth.

cylindrical gear with curvilinear shape teeth;UG/Open Grip;parametric modeling;dynamics

1001-2265(2016)04-0012-04DOI:10.13462/j.cnki.mmtamt.2016.04.004

2015-05-18；

2015-06-22

國家自然科學基金項目資助(51375320)

賀林莉(1989—)，男，湖南衡陽人，四川大學碩士研究生，研究方向為機械傳動，機電一體化，(E-mail)scuhelinli@163.com。

TH132 ；TG506

A