基于SIMULINK的車輛防抱死制動系統控制研究

李振興　周晶晶

摘要： 利用Simulink軟件建立車輛防抱死制動系統的仿真模型；基于PID控制原理設計以車輪滑移率為控制對象的防抱死制動系統控制器，對防抱死制動控制系統進行仿真。將普通制動系統與防抱死制動系統仿真結果進行對比，結果表明PID控制的防抱死制動系統能有效提高車輛的方向操縱性和制動效能。

Abstract： Firstly， the simulation model of Anti-lock braking system is established by the software of simulink； Secondly， this paper designs a kind of Anti-lock Braking System（ABS） controll system and targeted at the wheel slip ratio based on the PID control strategy， which simulated the system of ABS and analysed the result. The simulation results of the ordinary brake system is contrasted with the Anti-lock braking system， and the results show that PID control ofAnti-lock braking system can effectively improve the direction of the vehicle maneuverability and braking performance.

關鍵詞： 防抱死制動系統；PID；仿真

Key words： anti-lock brake system；PID；simulation

中圖分類號：U463.33 文獻標識碼：A 文章編號：1006-4311（2016）07-0102-03

0 引言

汽車防抱死制動系統是提高車輛行駛安全的重要裝置[1]。它能防止車輛在制動時車輪抱死滑移，保障車輛的行駛穩定性和轉向操縱性，同時能有效地縮短制動距離，減少交通事故的發生。

防抱死制動系統中最重要的部件是防抱死制動控制器，它決定了防抱死制動系統系統的性能，而控制器的核心是控制算法的選擇。目前大部分車輛上采用的是基于經驗的邏輯門限控制方法，它的方法簡單實用，但調試比較困難，采用經驗的方法，不同的車輛需要不同的匹配技術，需要比較多的道路試驗加以驗證，算法實施復雜而且魯棒性不強。PID控制算法原理簡單，使用方便；適應性強；魯棒性強。因此，應用PID控制理論，在SIMULINK中仿真研究防抱死制動系統的控制策略及其控制效果。

1 系統模型建立

1.1 單輪車輛模型

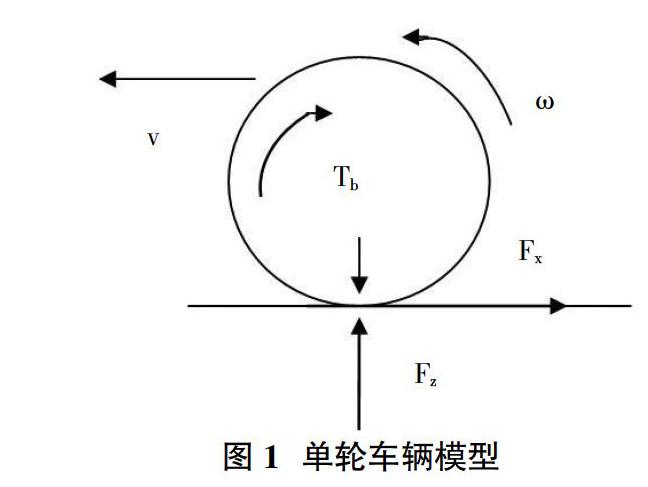
為簡化研究問題，采用單輪車輛系統模型如圖1所示，忽略空氣阻力和車輪滾動阻力；車輛質量均勻分布在每個車輪上，輪胎的機械特性相同；車輛在水平公路上行駛[2]。

根據圖1，得到車輛動力學方程：

式（1）～（3）中：m為1/4車輛質量；v為車輛縱向速度；Fx為車輪縱向附著力；I為車輪轉動慣量；？棕為車輪轉動角速度；R為車輪半徑；Tb為制動力矩；？滋為車輪與地面間的附著系數；Fz為地面對車輪支撐力。

1.2 車輪輪胎模型

輪胎模型是指車輛在制動過程中，附著系數和各相關參數之間的函數關系[3]。輪胎的附著系數受多種因素影響，除了滑移率，還有輪胎的花紋、材料及路面的狀況等。在實際情況下，人們在建立輪胎模型時很難將所有的影響因素都考慮進去，只考慮了對附著系數影響大的因素。目前，人們常用的輪胎模型有魔術公式輪胎（經驗公式模型）和雙線性公式模型（半經驗公式模型）兩種[4]。

采用雙線性公式模型，其擬合精度較高，計算方便，比較適合用于模擬仿真研究。

表達式如下：

滑移率的表達式如下：

滑移率常用來衡量制動時車輪的滑移程度，車輪在純滾動時滑移率為0；車輪抱死在純滑動時滑移率為100%；車輪邊滾動邊滑動時滑移率在0～100%之間。實驗證明，滑移率在15%～20%時附著系數最大，制動效果最佳。

1.3 車輛制動系統模型

制動系統模型包括傳動機構模型和制動器模型兩部分。采用液壓傳動機構，為簡化模型，忽略壓力傳送的延遲因素和電磁閥環節，液壓傳動系統簡化為一階慣性環節和一個積分環節[6]。由于電磁閥的響應時間通常小于等于10 ms，所以液壓傳動系統的一階慣性環節的傳遞函數為：

制動器模型指的是制動器力矩和制動液壓之間的關系的模型，建模前假定制動器為理想的元件，理解為其非線性特性比較弱且不計其滯后所產生的影響。制動器表達式如下：

2 PID控制器設計

PID控制器是一種線性控制器，是根據設定值與實際輸出值的偏差作為控制器的輸入信號。PID的控制算法如下式：

式（8）中，Kp為比例放大系數，比例系數增大，控制系統的余差減小，但振蕩加劇；Ki為積分系數，其數值過大，降低控制系統的穩定性；Kd為微分系數，其數值增大，減小系統的超調量，減小調節時間，但過強會導致系統穩定性降低。

設計的PID控制器是以車輪滑移率為控制目標，通過傳感器采集汽車行駛過程中的車速和輪速信息，計算出車輪的實際滑移率。車輪的實際滑移率與期望滑移率之間的差值即為PID控制器的輸入，輸出為制動器壓力。控制策略如圖2所示。

比例系數、積分系數和微分系數的參數選擇決定了PID控制器的控制效果。按照先比例，再積分，最后微分的順序進行參數的設定。經多次調試后的PID控制器的參數為Kp=230，Ki=200，Kd=3。期望滑移率為0.2。根據上述控制策略和參數，設計PID控制器仿真模塊如圖3所示。

3 控制系統仿真

根據上述車輛模型數學表達式及設計的PID控制器，在SIMULINK軟件中建立防抱死制動控制系統仿真模型，模型如圖4所示。

選取某轎車為研究對象，主要仿真參數如下：1/4車輛質量=390kg；車輪半徑R=0.268m；車輪轉動慣量I=1.4852kg·m2；初始車速v=20m/s；路面參數選擇高附著系數。求解器選取變步長模式ode45s，仿真時間設定為3秒。

4 仿真結果與分析

制動系統的性能評定指標有：制動距離、制動時間、車輪滑移率、制動減速以及制動時地面的附著系數等。

在仿真結果中選取車輪滑移率與時間關系曲線；制動減速度與時間關系曲線；地面附著系數與時間關系曲線；車速&輪速與時間關系曲線以及制動距離。對比普通制動系統與有PID控制的防抱死制動系統的仿真結果，如圖5～9所示。

從圖5～9可以看出，在沒有防抱死制動控制的普通制動情況下，車速從20m/s到車輛完全停止經過了2.97秒，而輪速經過0.22秒后就下降到0，同時滑移率為1，車輪出現抱死狀況。制動距離為30.29m，制動減速度在6.85左右，同時地面的附著系數為0.7。加入PID防抱死制動控制環節后，車輛由初始速度20m/s到車輛停止用時為2.65秒，整個制動過程中，車輪轉速沒有迅速下降到0，而是隨著車速一起變為0，車輪沒有出現抱死狀況，并且車輪滑移率始終在期望值0.2附近。制度距離為27.45m，制動減速度在7.85左右，同時地面的附著系數為0.8。由此可見PID控制下的防抱死制動系統具有良好的控制效果，與常規制動相比，制動時間縮短了10.7%，制動距離減少了9.4%，同時滑移率在期望值附近，并且在整個過程中無較大波動情況，穩定性較好。

5 結語

在制動系統車輛模型的基礎上，運用PID控制理論，基于SIMULNK平臺研究以滑移率為控制目標的車輛防抱死制動系統。通過仿真對比分析，PID控制的防抱死制動系統能有效的提高車輛制動時的方向操縱性和制動效能。

參考文獻：

[1]余志生.汽車理論[M].北京：機械工業出版社，2000.

[2]喻凡.車輛動力學及其控制[M].北京：人民交通出版社，2004.

[3]程軍.汽車防抱死制動系統的理論與實踐[M].北京：北京理工大學出版社，1999.

[4]葉磊，尹作發.基于Matlab/Simulink的車輛制動過程分析[J].公路與汽運，2006（6）：5-7.

[5]M.Gavas， M.Izciler. Deep drawing with anti-braking system（ABS）[J]. Mechanism and Machine Theory， 2006，Vol41（12）：1467-1476.

[6]程軍.汽車防抱死制動系統的控制方法分析[J].汽車技術，1992（10）：1-8.