機翼顫振的時滯反饋控制研究

羅夢翔， 高明周， 蔡國平

(上海交通大學 船舶海洋與建筑工程學院，上海　200240)

?

機翼顫振的時滯反饋控制研究

羅夢翔， 高明周， 蔡國平

(上海交通大學 船舶海洋與建筑工程學院，上海200240)

采用瞬時最優方法對二元機翼顫振的時滯反饋控制進行研究。首先采用Lagrange方法建立機翼系統的顫振動力學模型，其中考慮了機翼俯仰剛度的立方非線性，然后采用瞬時最優控制方法進行了非線性時滯反饋控制律的設計，最后通過數值仿真對控制方法的有效性進行了驗證。仿真結果顯示，時滯控制律能夠有效地抑制機翼的顫振。

機翼；顫振；瞬時最優控制；時滯

飛行器顫振是在其本身運動引起的氣動力的激勵下發生的一種自激振動。當飛行器的飛行速度超過臨界顫振速度時，機翼會不斷地從氣流中吸取能量，導致振動無法衰減下來，從而給飛行器帶來災難性的破壞。目前機翼顫振問題已經得到越來越多學者的大量關注，并有許多研究成果問世。例如，于明禮等[1-2]考慮機翼外部擾動和建模誤差的不確定性，分別設計了H∞魯棒控制律和μ控制器，并進行了風洞實驗驗證；WANG等[3]針對含未建模非線性以及外接擾動的二元非線性氣動彈性系統，采用高增益狀態觀測器設計多輸入多輸出(Multiple-Input Multiple-Output,MIMO)自適應輸出反饋控制器，進而抑制結構氣動彈性響應和極限環震蕩；錢文敏等[4]針對氣動彈性系統中由于來流速度擾動引起的不確定性，發展了一種新的不確定性建模方法，該方法從氣動彈性建模的根源出發，運用信號變換法則使系統的不確定維數得以降低，進而設計出更為有效的顫振魯棒控制系統。

然而在主動控制系統中不可避免地存在著時滯現象，控制回路中包含有作動器、傳感器和控制器等電子元器件，這些電子元件的動態特性會導致最終作用于結構的控制力產生時滯。已有研究結果顯示，即使是小時滯量，也會導致在系統不需要能量時作動器向系統輸入能量，從而有可能引起控制效率的下降或控制系統失穩。對于機翼顫振主動控制，目前已有一些學者開始關注控制系統中的時滯問題，例如，ZHAO[5]研究了在不可壓流場中時滯對主動控制機翼顫振穩定性的影響，發現在控制回路中，時滯對整個伺服氣彈系統有著重要的影響，同時證明了時滯對系統穩定的影響主要與系統的參數和反饋信號的類型有關；LIBRESCU等[6]運用Pontryagin方法結合Stepan定理研究了非線性時滯對氣彈系統的影響，發現通過適當的設計，時滯控制比傳統的控制方法能夠更有效的抑制顫振；YUAN等[7]針對二維高超音速升力面設計了Pyragas型的時滯反饋控制器，分析了受控系統的非線性氣動彈性行為；HUANG等[8]通過離散化狀態方程，將含輸入時滯的狀態方程轉化為無時滯的狀態方程，并在此基礎上運用LQG(Linear Quadratic Gaussian)控制方法和卡爾曼觀測器進行計入時滯的機翼顫振控制。在此值得說明的是，對于機翼顫振問題，目前絕大多數的研究工作是集中在主動抑制方法上，而關于其中時滯問題的研究非常少。飛行器的飛行速度一般很高，在非常短的時間間隔里系統的狀態也會出現很大不同，因此非常小的時滯量也會對控制性能造成大的影響。可以說，關于機翼顫振主動控制中的時滯問題還有許多問題有待研究。

本文對機翼顫振的時滯反饋控制方法進行研究，其中考慮了機翼剛度的立方非線性，控制律的設計采用瞬時最優控制方法進行設計，最后通過數值仿真對所給方法的有效性進行了驗證。

1　顫振模型建立

二元機翼的模型見圖1，機翼展長為s，弦長為c。機翼根部有兩個轉動彈簧分別提供沉浮h(向下為正)和俯仰θ(機翼前緣抬頭為正)兩個自由度運動，它們的彈簧剛度分別為Kh和Kθ，這兩個自由度之間無剛度耦合。Q和P分別為氣動中心和彈性軸，xf為機翼前緣到彈性軸的距離，氣動中心和彈性軸的距離為ec，e為偏心率。操縱面還有一個偏轉自由度β(向下為正)，當操縱面的鉸接剛度足夠大時，可以忽略操縱面慣性的影響，二元機翼退化成兩個自由度，操縱面僅作為一個激勵裝置，與機翼基本氣動升力無關，且可以偏轉到任意期望的角度[9]。

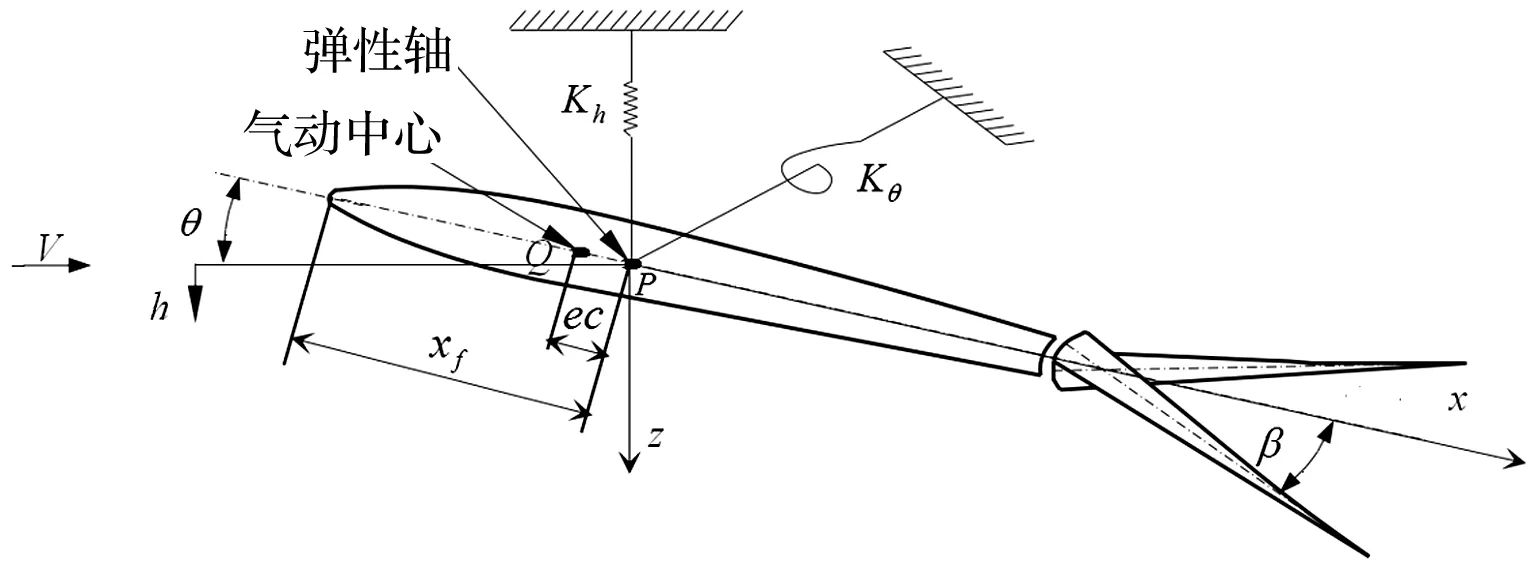
圖1　帶操作面的二元機翼模型Fig.1　Two-dimensional airfoil model with control surface

機翼上任意一點在垂直方向的位移(向下為正)為：

z=h+(x-xf)θ

(1)

系統動能、勢能以及耗散能分別為：

(2)

(3)

(4)

式中：m為機翼單位面積質量，Ch和Cθ分別為沉浮和俯仰兩個自由度彈簧的阻尼。

采用片條理論得到機翼每個片條元上簡化的氣動升力和繞彈性軸氣動力矩分別為[9-10]：

(5)

(6)

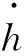
作用在翼面的氣動力和氣動力矩做的虛功為：

δW=∫[-dLδh+dMfaδθ]

(7)

因此，廣義力可表示為：

(8)

(9)

將系統動能、勢能、耗散能及廣義力代入拉格朗日方程，可得二元機翼氣彈運動方程為：

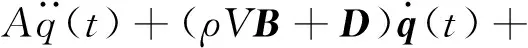
(ρV2C+E)q(t)=0

(10)

式中：q(t)=[h(t),θ(t)]T為浮沉和俯仰自由度的廣義坐標向量；A、B、C、D和E分別為機翼系統的慣性、氣動阻尼、氣動剛度、結構阻尼和結構剛度矩陣，表達如下：

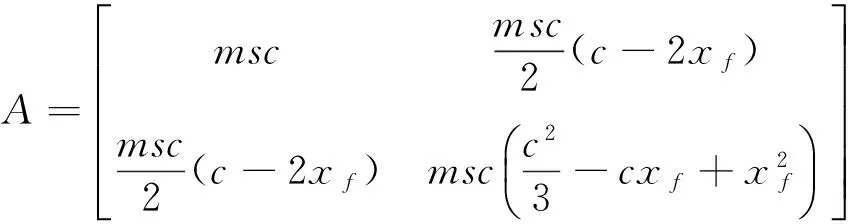
操縱面偏轉角β改變會產生氣動升力Lc和氣動力矩Mc，操縱面的控制力為：

(11)

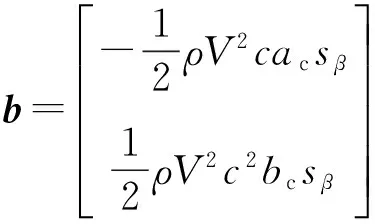
彈性機翼的大變形會導致結構立方非線性，也就是說此時剛度非線性與立方硬彈簧特性具有類似的動力學特性。考慮俯仰剛度的立方非線性特征，即：

M(θ)=Kθθ+enlKθθ3

(12)

式中：enl為非線性剛度系數。將系統的動能、勢能、耗散能、考慮了俯仰剛度立方非線性以及操縱面的控制力代入拉格朗日方程中，可以得到：

f(t)=bβ

(13)

式(13)可化為：

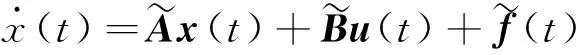
(14)

式中：

2　瞬時最優時滯反饋控制

式(14)是一個標準的非線性狀態方程，這里我們采用由YANG等[11]提出的瞬時最優控制方法設計非線性控制律。對于時滯反饋控制律的設計方法，文獻[12]中有詳細地介紹。

在式(14)中考慮控制項的時滯，則系統的時滯狀態方程為：

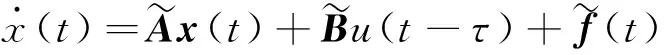
(15)

式中：τ為時滯量。以下針對狀態方程式(15)設計時滯反饋控制律。

對式(15)進行如下的積分變化[13]：

(16)

從而可以將式(15)轉化為如下不顯含時滯的非線性狀態方程形式：

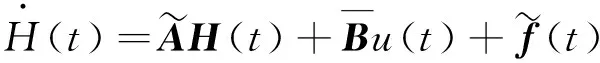
(17)

瞬時最優控制是一種基于四階Runge-Kutta算法的控制設計方法，它可以處理非線性系統的控制設計。對式(17)采用四階Runge-Kutta法，其解可以寫成如下形式：

(18)

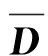
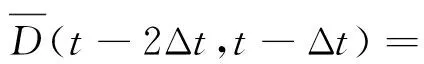
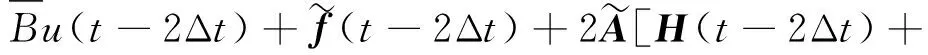
(19)

式中：A0、A1、A2及A3表達如下：

(20)

取如下性能指標：

J(t)=HT(t)QH(t)+uT(t)Ru(t)

(21)

式中：Q為非負定對稱矩陣，R>0為任意正數。瞬時最優控制設計是在式(18)的約束下設計控制律，使得每一步的性能指標J取極小值。為此，定義如下Hamilton函數：

YH=HT(t)QH(t)+uT(t)Ru(t)+

(22)

式中：λ為Lagrange乘子列陣。通過：

(23)

可以得到瞬時最優控制律為：

(24)

由式(24)可知，控制律u(t)是H(t)的函數，而由式(16)可知,H(t)包含有積分項，該積分項的詳細迭代計算格式可參考文獻[13]。

3　數值仿真

本文在此進行數值仿真，驗證所給方法的有效性。二元機翼結構參數見表1。首先采用V-g法[14]確定機翼的臨界顫振速度。圖2為風速V和人工阻尼g之間的關系。V-g法中人工阻尼g的物理意義為：假如機翼的真實結構阻尼正好等于這個g值，則在所設定的風速V和空氣密度ρ的狀態下機翼做簡諧振動。由圖2可知，當速度達到V=509.08 m/s時，俯仰角對應的g值穿過零點，由負值變為正值，故此顫振臨界速度為V=509.08 m/s，機翼速度大于該值將發生顫振。

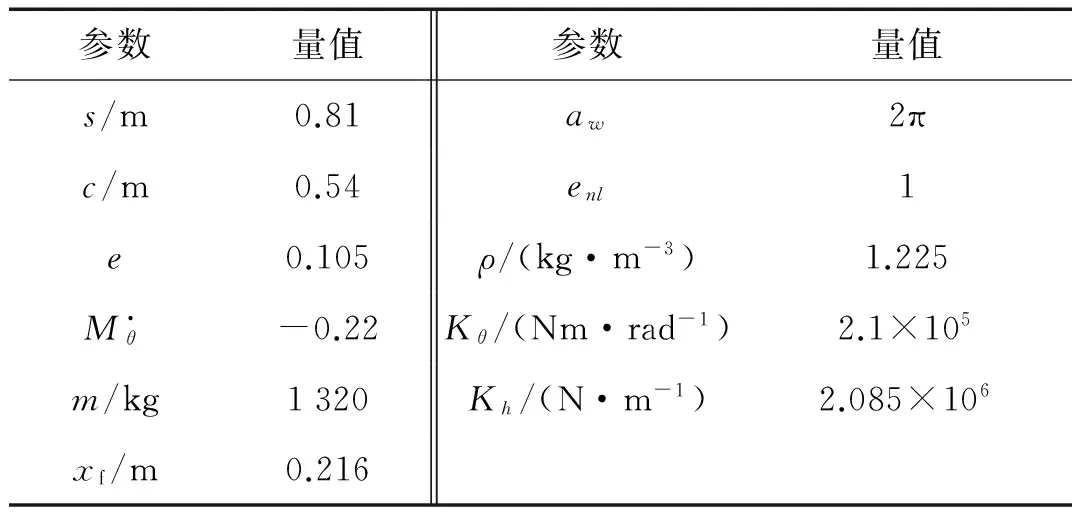
表1　二元機翼結構參數

數值仿真中取風速為600 m/s，該值大于臨界顫振速度。假定機翼有一個初始的沉浮位移h=0.5 m和初始俯仰角度θ=0.05°。為了顯示本文所給時滯處理方法的有效性，本文在此考慮大時滯量問題，控制系統中的時滯量取值為τ=0.1 s。控制設計時，取式(21)中控制增益為Q=I4×4和R=10。由于控制信號是操縱面的偏轉角度，本文中要求最大偏轉角為±5°。圖3為施加時滯反饋控制后機翼的沉浮位移、 俯仰角和操縱面偏轉角時程，不施加控制的結果也在圖中予以顯示。從圖3可知，當對機翼不施加任何控制措施時，沉浮位移在氣動阻尼的影響下會逐漸衰減；由于系統中存在立方非線性，當風速超過臨界顫振速度時，俯仰角響應在原點附近出現穩定的周期解，產生極限環顫振，這種情況容易使機翼產生疲勞斷裂。施加時滯反饋控制后，機翼的響應能夠在很短的時間內得到抑制。在此需要說明：當時滯量取小于0.1 s的任意值時，本文中的時滯處理方法都能夠有效地抑制機翼系統的顫振。

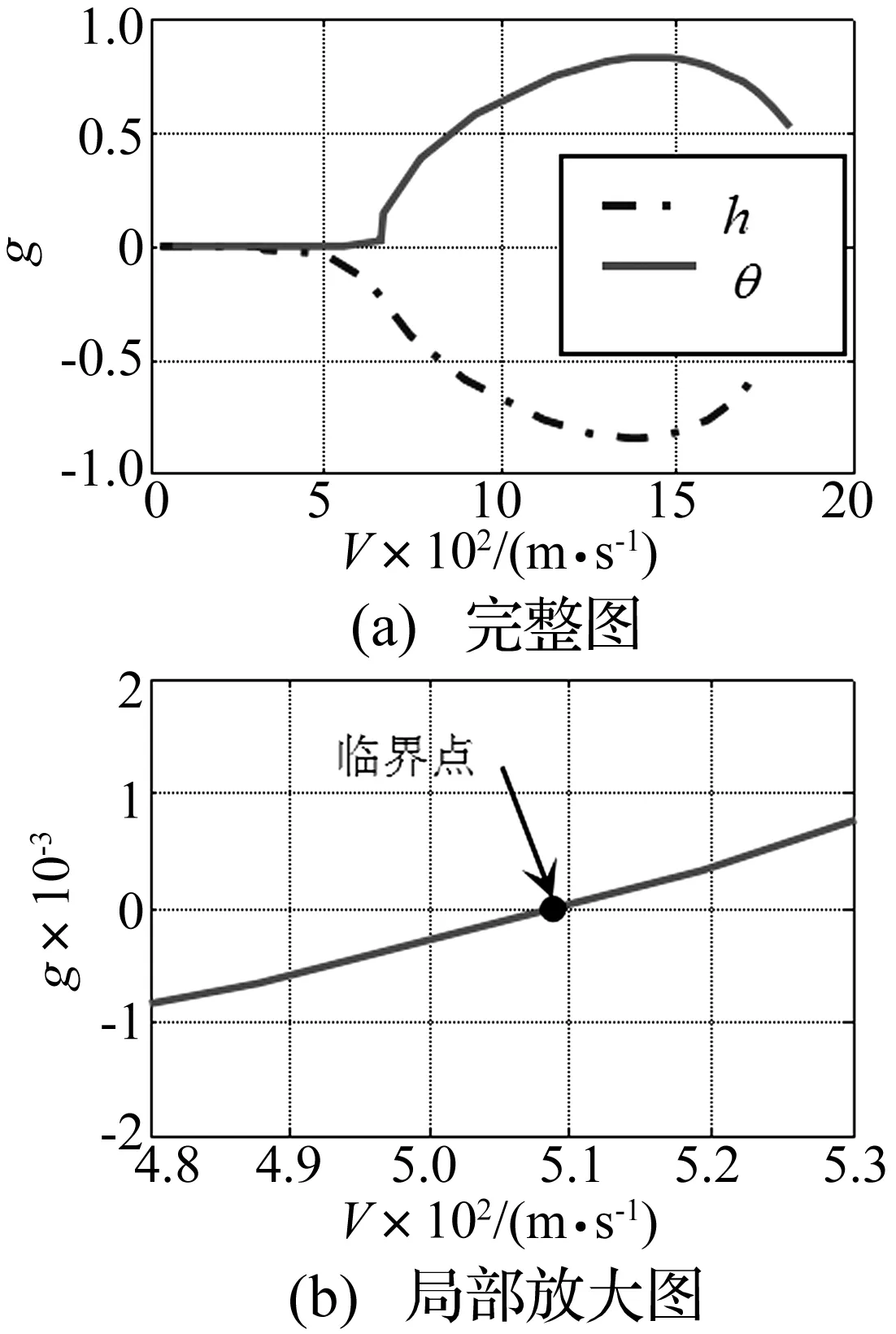
圖2　風速與人工阻尼關系Fig.2　Relation of wind speed and artificial damping

圖3　控制仿真結果Fig. 3 Control simulation results

4　結　論

本文對二元機翼顫振的時滯反饋控制進行了研究，給出了機翼顫振系統的動力學模型，采用瞬時最優控制方法進行了時滯反饋控制律的設計，數值仿真中采用V-g法獲得了機翼的臨界顫振速度。仿真結果顯示出，本文所給出的時滯問題處理方法能夠有效地處理控制系統中的時滯，時滯反饋控制律能夠有效地抑制機翼的顫振。

[1] 于明禮, 文浩, 胡海巖. 二維翼段顫振的H∞控制[J]. 振動工程學報, 2006, 19(3): 326-330.

YU Mingli, WEN Hao, HU Haiyan. Active flutter suppression of a two-dimentional airfoil using H∞synthesis [J]. Journal of Vibration Engineering, 2006, 19(3): 326-330.

[2] 于明禮, 文浩, 胡海巖, 等. 二維翼段顫振的μ控制[J]. 航空學報, 2007, 28(2): 340-343.

YU Mingli, WEN Hao, HU Haiyan, et al. Active flutter suppression of a two dimensional airfoil section usingμsynthesis [J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 340-343.

[3] WANG Z, BEHAL A, MARZOCCA P. Model-free control design for multi-input multi-output aerolastic system subject to external disturbance [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 446-458.

[4] 錢文敏, 趙永輝, 胡海巖. 二元機翼/外掛系統的顫振魯棒抑制[J]. 中國科學: 物理學, 力學, 天文學,2013,43(4):334-344.

QIAN Wenmin, ZHAO Yonghui, HU Haiyan. Robust flutter suppression for a 2-dimensional wing-store system [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2013, 43(4): 334-344.

[5] ZHAO Y H. Stability of a time-delayed aeroelastic system with a control surface [J]. Aerospace Science and Technology, 2011, 15(1): 72-77.

[6] LIBRESCU L, MARZOCCA P. Aeroelasticity of 2D lifting surfaces with time-delayed feedback control [J]. Journal of Fluids and Structures, 2005, 20: 197-215.

[7] YUAN Y, YU P, LIBRESCU L, et al. Aeroelasticity of time-delayed feedback control of two-dimensional supersonic lifting surfaces [J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 795-803.

[8] HUANG R, HU H, ZHAO Y. Designing active flutter suppression for high-dimensional aeroelastic systems involving a control delay [J]. Journal of Fluids and Structures, 2012, 34: 33-50.

[9] 王囡囡. 二元機翼顫振及其主動控制的研究[D]. 徐州：中國礦業大學, 2013.

[10] BISPLINGHOFF R L, ASHLEY H. Principles of aeroelasticity [M]. New York: Courier Dover Publications, 1962.

[11] YANG J N, LI Z, DANIELIANS A, et al. Aseismic hybrid control of nonlinear and hysteretic structures II [J]. Journal of Engineering Mechanics, 1992, 118(7): 1441-1456.

[12] 蔡國平, 陳龍祥. 時滯反饋控制的若干進展[J]. 力學進展, 2013, 43(1): 21-27.

CAI Guoping, CHEN Longxiang. Some problem of delayed feedback control [J]. Advances in Mechanics, 2013,43(1):21-27.

[13] CAI G P, HUANG J Z. Instantaneous optimal method for vibration control of linear sampled-data systems with time delay in control [J]. Journal of Sound and Vibration, 2003, 262(5): 1057-1071.

[14] 趙永輝. 氣動彈性力學與控制[M]. 北京：科學出版社, 2007.

Delayed feedback control for airfoil flutter

LUO Mengxiang, GAO Mingzhou, CAI Guoping

(School of Naval Architecture and Ocean Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The delayed feedback control for a two-dimensional airfoil flutter was investigated. The dynamic equation for airfoil flutter was established using the Lagrange equation, in which the cubic nonlinearity describing the wing pitching stiffness was taken in account. Then the instantaneous optimal control method was used to design a nonlinear delayed feedback controller. Finally, numerical simulations were carried out to demonstrate the effectiveness of the proposed controller. The simulation results indicate that the delayed feedback controller proposed can effectively suppress the airfoil flutter.

airfoil; flutter; instantaneous optimal control; time delay

國家自然科學基金(11132001;11272202;11472171);上海市教委科研重點項目(14ZZ021);上海市自然科學基金(14ZR1421000)

2015-04-17修改稿收到日期：2015-08-31

羅夢翔 女，碩士生，1992年生

蔡國平 男，博士，教授，1956年生

V214.3

A DOI:10.13465/j.cnki.jvs.2016.14.010