考慮油膜不確定性的滑動軸承-轉子系統不平衡量識別

毛文貴， 李建華， 劉桂萍， 劉　杰

(1.湖南工程學院 機械工程學院，湖南省風電裝備與電能變換協同創新中心，湖南 湘潭　411101；2. 湖南大學 機械與運載工程學院,長沙　410082)

?

考慮油膜不確定性的滑動軸承-轉子系統不平衡量識別

毛文貴1,2， 李建華1， 劉桂萍2， 劉杰2

(1.湖南工程學院 機械工程學院，湖南省風電裝備與電能變換協同創新中心，湖南 湘潭411101；2. 湖南大學 機械與運載工程學院,長沙410082)

針對滑動軸承-轉子系統不平衡量識別過程中滑動軸承油膜特性系數的不確定性，提出了考慮油膜不確定性的轉子系統不平衡量的識別方法。該方法考慮滑動軸承油膜特性系數為不確定因素，基于區間數學理論和一階泰勒級數展開式的區間法將具有不確定性結構的不平衡量識別問題轉化為兩類確定性結構的不平衡量識別問題；對于確定性結構的不平衡量識別問題根據滑動軸承-轉子系統運行時不平衡量是以不平衡力的形式作用于主軸上，提出將不平衡力在時域內用一系列的脈沖函數來表示，利用滑動軸承-轉子系統的瞬態響應分析方法來構建正問題，結合正則化方法處理不平衡量識別中的病態問題，獲得轉子系統不平衡量的上邊界和下邊界。通過一轉子實驗臺檢驗了不平衡量識別方法的有效性和魯棒性。

滑動軸承-轉子系統;不平衡量識別;不確定性;油膜特性系數;區間法

滑動軸承-轉子系統在高檔數控機床中得到了廣泛地應用。滑動軸承油膜特性系數、主軸系統不平衡量等動力學關鍵特性參數與滑動軸承-轉子系統響應之間存在著非常復雜的關系，直接影響著機床的加工精度。但對于主軸而言，由于制造、安裝誤差以及材料的不均勻性等因素，不平衡量的存在是必然的。在滑動軸承-轉子系統中，不平衡量按照一定的標準分成不同的等級，并給出具體的動載荷表達形式，但由于結構本身的動力特性是設計變量或控制參數的非線性函數，存在對動載荷的敏感性。因此，規范或標準中的設定載荷模式與結構所受的實際的動態載荷有偏差時，進行結構的動力特性分析和優化設計就可能與實際情況存在較大的偏差。在未能給出不平衡量的確切值時，會給滑動軸承-轉子系統的動力特性優化設計和健康監測與故障診斷等問題的研究帶有一定的盲目性。因此，不平衡量的準確獲取能為這些問題的研究提供確切的載荷條件，對結構的安全性和可靠性設計具有重要的實際意義。了解不平衡量對滑動軸承-轉子系統響應的影響，準確識別不平衡量，是實現滑動軸承-轉子系統動平衡和動態性能優化，降低回轉精度的關鍵。

然而由于加工條件和測試環境等一些復雜因素的影響，不平衡量的大小很難直接測量。而滑動軸承-轉子系統動力學響應(位移、速度和加速度等)的測量相對容易和準確些，所以利用測量的響應對不平衡量識別的研究是非常必要的。劉淑蓮等[1]基于全息譜分析的非線性轉子系統不平衡量識別，通過傅里葉展開和全息譜技術將油膜力和不平衡量的工頻的周期力分開來獲得轉子工作轉速下的不平衡量。同時隨著計算機技術的發展，人們也開始在不平衡量識別中注入遺傳算法、神經網絡和計算反求技術。利用不同的激勵通過實驗與理論計算來間接獲得剩余不平衡量[2-4]。TIWARI等[5]利用脈沖和不平衡響應同時識別多自由度柔性轉子-軸承系統的剩余不平衡量和油膜特性系數。不平衡量在滑動軸承-轉子系統運行時以力的形式作用在主軸結構上，因此，不平衡量識別可轉化為不平衡力識別問題來研究[6]。而利用測量的響應進行載荷求解的動載荷識別技術正日益成為工程實際中動載荷獲取的不可或缺的一種重要手段，對其研究在軸承-轉子系統的動平衡控制、故障診斷和檢測等諸多技術領域都有廣泛的應用前景[7-8]。載荷識別問題作為結構動力學的第二類反問題，國內外的研究雖然取得了一定的成果[9-10]，但上述方法識別不平衡量時一般都假定系統模型是確定的。然而滑動軸承-轉子系統的不平衡量直接影響滑動軸承的油膜特性。理論上不平衡量變化時，滑動軸承軸頸處的作用力會發生變化，軸頸中心移動，從而油膜特性系數會發生變化。即滑動軸承-轉子系統不平衡量識別所對應的結構具有不確定性。因此，研究滑動軸承-轉子系統不確定結構的不平衡量識別問題，正確客觀地估計和評價油膜不確定性因素對不平衡量識別反問題解的存在性、唯一性、穩定性等的影響，在學術研究上具有一定的理論研究價值。同時，如果能從區間角度對油膜不確定性進行度量，在此基礎上再進行不平衡量識別，則有望能在綜合考慮不確定性影響因素下給出滑動軸承-轉子系統所受不平衡量的統計特性的上、下邊界，這能更加合理地評價結構的不平衡量，為滑動軸承-轉子系統的動平衡研究提供可靠的輸入條件。基于區間方法[11]提出一種基于區間的滑動軸承-轉子系統不平衡量識別方法，考慮滑動軸承油膜特性系數為不確定變量時對不平衡量識別結果的影響。

1　不平衡量識別問題的描述

本文提出的滑動軸承-轉子系統不平衡量的識別是在滑動軸承-轉子系統瞬態響應分析的基礎上進行的。滑動軸承-轉子系統的瞬態響應方程見式(1)。

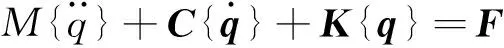
(1)

式中：q為轉子軸心位移；阻尼矩陣C包含了滑動軸承的阻尼系數CB；剛度矩陣K包含了滑動軸承的剛度系數KB；M為質量矩陣。力矩陣F由質心偏離幾何中心而產生的不平衡力組成。

即由可測知的滑動軸承-轉子系統瞬態響應，結合式(1)的瞬態響應方程，建立包括不確定油膜特性系數的不平衡量識別方程。當滑動軸承-轉子系統的滑動軸承油膜剛度和阻尼系數通過有限變分法[12]計算，而轉子軸心位移通過測量獲取，則式(1)中只有右邊的不平衡力是未知數。而不平衡力也可由式(2)表示。

A=mrω2

(2)

式中：t為時間；ω為角速度；A為不平衡量幅值；φ為不平衡量相位。m為不平衡質量；r為不平衡質量距軸中心的距離;fx,fy為不平衡力在x，y兩方向的分力。

由式(2)可知，根據不平衡力fx,fy可獲得不平衡量幅值A和相位φ，從而可以識別出不平衡量。

但滑動軸承油膜剛度和阻尼系數計算時，其大小與作用在軸頸上的外力有關，而滑動軸承-轉子系統的不平衡量大小會影響作用在軸頸上的外力，從而影響滑動軸承油膜剛度和阻尼系數的大小。即滑動軸承-轉子系統不平衡量識別時，滑動軸承油膜特性系數具有不確定性。因此，滑動軸承-轉子系統不平衡量識別是具有不確定性結構的不平衡量識別問題。

2　不確定性結構的不平衡量識別方法

2.1考慮油膜特性系數不確定性區間法

目前對不確定變量的描述方法主要有區間法和概率法[13-16]，依據概率法進行不平衡量識別時，本案例中構建滑動軸承油膜特性系數的概率密度函數需要大量的樣本數據，這在實際中不太現實。而根據經驗，滑動軸承油膜特性系數大概的區間范圍還是可以確定的。因此，采用區間法，并基于一階泰勒級數展開式的區間法將具有滑動軸承油膜特性系數為不確定變量的滑動軸承-轉子系統的不平衡量識別方法轉化為滑動軸承-轉子系統中兩類滑動軸承油膜特性系數為確定變量的不平衡量識別問題，即不確定變量中點處的不平衡量識別和不平衡量對于油膜不確定性變量的梯度的識別。

以脈沖信號作為單元信號，將不平衡量表現的不平衡力在時域里表示為一系列脈沖函數的疊加。對于一個線性系統，在連續時間域內當只受單個不平衡力時，滑動軸承-轉子系統的瞬態響應能表示成式(3)所示的卷積分形式。

(3)

式中：q(t)為測點z處的瞬態響應(位移、速度或加速度等);f(t)為作用在滑動軸承-轉子系統上的不平衡力的時間歷程;g(t)為相應的由不平衡力作用點到瞬態響應測點的Green函數。

當考慮不確定變量時，滑動軸承-轉子系統的瞬態響應方程式(3)變為式(4)：

(4)

式中：λ為滑動軸承-轉子系統中的不確定變量;核函數g(t,λ)為包容不確定變量λ的集合，因此，不平衡力不再是一個解，而是一個解集。基于區間分析方法，基于測量瞬態響應的不確定性結構的不平衡力對于任一時刻不再是實數，而是一個與不確定變量一一對應的有界區間，即：

f(t,λ)∈fI(t)=[fI(t),fR(t)]

(5)

式中：fI(t)為t時刻的不平衡力區間;其下邊界fL(t)和上邊界fR(t)為t時刻的不平衡力集合中的極小與極大值，表達如式(6)。

(6)

實際工程中關心的往往是這個解集的上下邊界，并不需要求解出所有的可能值。不確定變量的下邊界λL和上邊界λR可以用區間的中點λc和半徑λw來描述，即

λ∈λI=[λI,λR]=[λc-λw,λc+λw],

(7)

不確定變量λ也可用下式描述：

λ=λc+δλ,δλ∈[-1，1]λw,

(8)

引入區間不確定性水平：

(9)

當不確定性水平較小時，將不平衡力在中點處進行一階泰勒級數展開，獲得式(10)如下

f(t,λ)=f(t,λc+δλ)≈

(10)

因此，在t時刻不平衡力上邊界fR(t)及下邊界fL(t)可顯式表達為:

(11)

(12)

2.2確定性結構的不平衡量識別

當結構的參數是確定時，確定性結構的滑動軸承-轉子系統的瞬態響應式(3)在時間域內用M個等間隔的采樣點進行離散，可轉化為方程式(13)所示的線性方程組。

(13)

用矩陣表達為式(14)。

q=G·F

(14)

式中：q為在時間域內對應的結構瞬態響應;G為Green函數;F為待識別的不平衡力。

對于多個不平衡力作用時，可以用同單個不平衡力作用時一樣的方法，并離散化為線性方程組形式。由于線性系統滿足疊加原理，可將多個不平衡力作用時的表達式轉化為式(15)的矩陣形式。

式(15)中N表示不平衡力的個數，對于多個不平衡力的識別，要求滑動軸承-轉子系統瞬態響應測點的個數不應小于不平衡力的個數，同時需要預先通過計算或實驗的方法得到各個不平衡力Fi到滑動軸承-轉子系統瞬態響應各測點qj之間相應的Green核函數矩陣Gij. 在瞬態響應矩陣q和核函數矩陣G已知的情況下，計算不平衡力矩陣F。結合式(2)可識別出多個不平衡量。

(15)

2.3正則化

在線性時不變假設下，時域內不平衡力可表示為一系列脈沖激勵核函數的疊加，而系統的響應能夠通過核函數的響應和不平衡力的卷積分得到。通過離散化卷積分，可以建立不平衡量識別的正向模型。滑動軸承-轉子系統中由于滑動軸承油膜的非線性使得不平衡量識別問題往往是不適定的和非線性的[17-18]。同時，通過實驗獲取的響應數據不可避免的存在測量噪聲，可能會使識別的不平衡量嚴重偏離真實解。不平衡量識別問題是不適定的。正則化方法能夠有效克服載荷識別過程中的病態性。只有不平衡量識別的穩定性滿足，反求的不平衡量才有實際意義。

當測量的響應數據中有誤差或噪聲時，引入正則化方法[19-21]，為了分析不平衡量識別過程中解的穩定性，需要考慮觀測數據中誤差或噪聲，所以將式(14)可以改寫成如下形式。

qδ=G·F+δ

(16)

式中:qδ為包含有噪聲的結構瞬態響應;F為理論上正確的不平衡力；δ為測量的瞬態響應所包含的噪聲。

然后，對核函數G進行如式(17)所示的奇異值分解(Singular Value Decom-Position,SVD)。

(17)

式中：U=[u1,u2,…,uk] 為G的左奇異向量和V=[v1,v2,…,vk] 為G的右奇異向量，是兩個標準化正交矩陣，Ω=diag(σi)為含有非負奇異值的對角矩陣。如果矩陣G的逆存在，利用式(17)可得估計的不平衡力F為[22-23]。

(19)

當濾波函數f(α,σi)采用如式(20) 濾波算子[24]為：

(20)

式(19)化為：

(GTG+αI)-1GTqδ

(21)

至此，結合式(21)和式(2)考慮噪聲的滑動軸承-轉子系統的不平衡量可穩定識別。通過區間法可將考慮不確定性結構的不平衡量識別問題轉化為考慮確定性結構的不平衡量識別問題。通過正則化方法處理測量中的噪聲引起的不平衡量識別的病態問題。將不平衡力在時域內用一系列的脈沖函數來表示，結合正則化方法穩定實現這兩類確定性變量的不平衡量識別問題的求解，并利用區間運算方法實現具有不確定性變量的滑動軸承-轉子系統的不平衡量上下邊界的確定。滑動軸承-轉子系統不確定性結構的不平衡量識別流程見圖1。

為避免識別問題的病態性，經常增加測點的數目(測點數不小于待識別參數的個數)或選擇對待識別參數變化敏感的測點，即選擇相關性強的測點。后者測試成本較低。本文用數值仿真模擬尋找不平衡量識別相關性強的測點。確定性結構的不平衡量識別的具體步驟如下：

(1) 根據滑動軸承-轉子系統實際情況，確定不平衡量的位置和數量，運用數值計算方法選擇強相關性響應測點的種類、位置和數量。建立滑動軸承-轉子系統的瞬態響應分析模型，施加不平衡量分析滑動軸承-轉子系統的瞬態響應，找到響應位移與所加不平衡量點有相關性強的響應測點，且響應測點的個數不能少于不平衡量的個數。

(2) 根據得到的響應測點，對要進行不平衡量識別的轉子實驗臺布置測試響應的傳感器。通過轉子實驗臺瞬態響應實驗測量上述測點處的動態響應qδ。

(3) 用滑動軸承-轉子系統瞬態響應方法求解不平衡量作用點到響應測點的核函數響應，并建立核函數矩陣G。

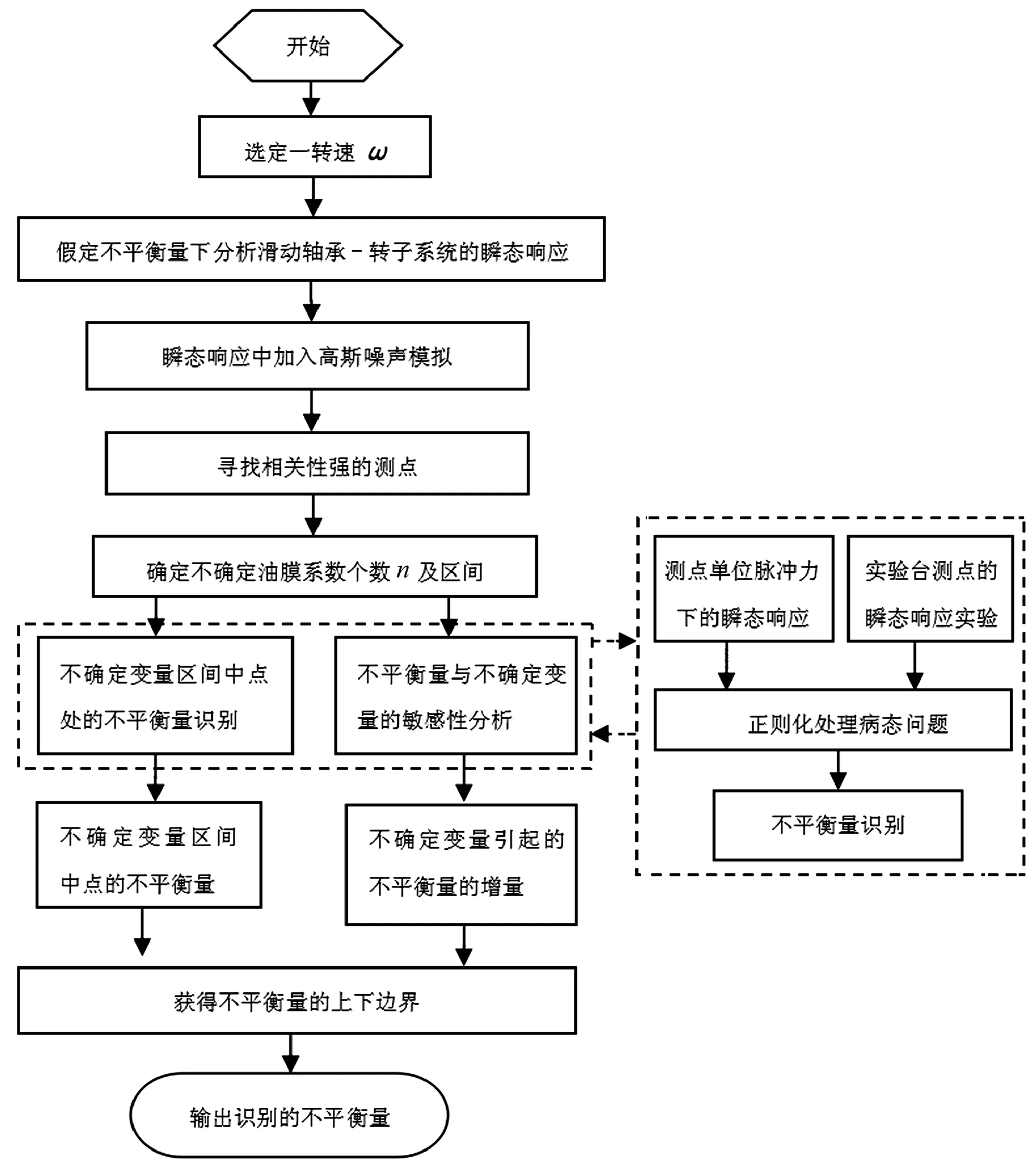
圖1　滑動軸承-轉子系統不確定性結構的不平衡量識別流程Fig.1　The identification method for the unbalance parameters of a rotor-bearing system

(4) 采用經典的正則化方法選擇TiKhonov或截斷奇異值分解(Truncated SVD,TSVD)等正則化算子f(α,σ),利用廣義交叉驗證(Generalized Cross-Validation,GCV)準則或L曲線方法確定合適的正則化參數α，將病態的核函數矩陣進行修正，記修正的核矩陣為Gα。

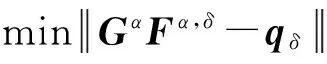
(6) 采用共軛梯度的LSQR方法進行迭代求解，從而獲得待識別的不平衡量，其中最佳的迭代次數可通過L曲線法來確定。

(7) 依據識別的實驗臺的不平衡量對實驗臺進行動平衡，比較實驗臺測點在動平衡前后的瞬態響應振幅大小來檢驗不平衡量識別結果。

3　應用實例

工程實際中對轉子進行動平衡時先要識別轉子不平衡量。動平衡的效果取決于不平衡量識別結果。本節用本文提出的滑動軸承-轉子系統不平衡量識別方法應用于轉子實驗臺的動平衡。

3.1實驗臺的瞬態響應分析

圖2為北京東方振動和噪聲技術研究所研制的實驗臺，由0～10 000 r/min直流電機驅動，由電機調速器數顯轉速，鍵相軸套產生鍵相信號，油膜滑動軸承2套，由油杯注油，圓盤直徑為80 mm,寬度為15 mm。轉軸為等截面軸，直徑為10 mm，軸長490.0 mm，轉子材料的密度為7 850 kg/m3，彈性模量為210 GPa，剪切彈性模量為80 GPa，轉速設計為2 000 r/min，滑動軸承為圓柱軸承屬于各向異性軸承，每個滑動軸承有8個油膜特性系數Kxx，Kxy，Kyx，Kyy，Cxx，Cxy，Cyx，Cyy左右兩個滑動軸承共有16個油膜特性系數，其油膜特性系數如表1。圓盤直徑60 mm處沿周向分布16個孔，可配置螺釘來人為設置不平衡質量，用光電傳感器測轉速，電渦流傳感器測位移。INV1612型轉子實驗臺，配合INV306U采集系統及INV1612 型多功能柔性轉子實驗系統軟件的可完成滑動軸承-轉子系統的瞬態響應實驗。

在轉速為2 000 r/min的情況下，通過渦流傳感器測得兩測點的位移瞬態響應見圖3。

圖2　INV-1612型轉子實驗臺Fig.2　The test rig of INV-1612

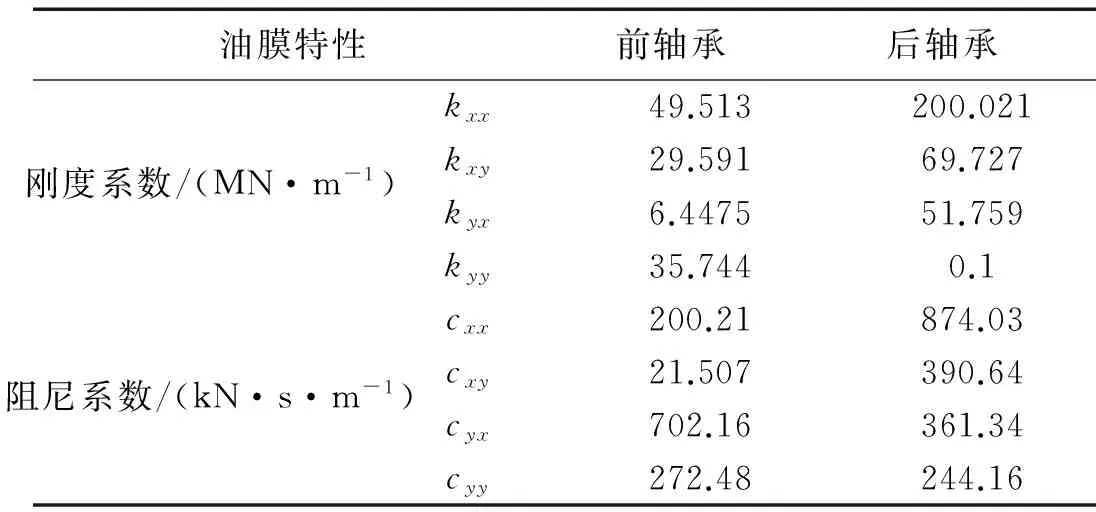
表1　滑動軸承油膜剛度和阻尼系數

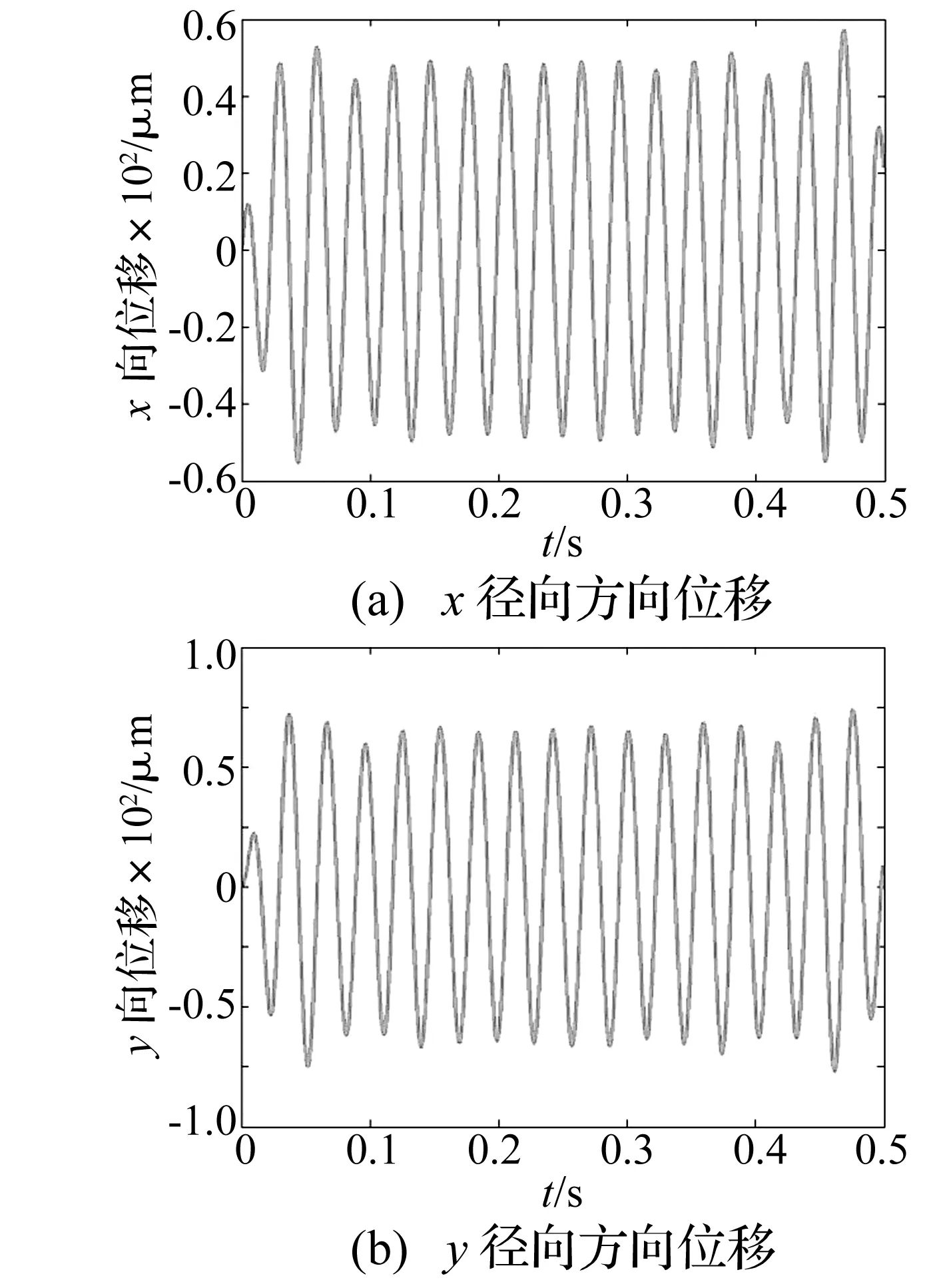
圖3　轉子實驗臺的位移響應Fig.3　Displacement responses of the test rig

3.2不考慮不確定變量的實驗臺不平衡量識別結果

針對測試的位移響應，用本文的滑動軸承-轉子系統不平衡量識別方法識別出實驗臺的不平衡量的力的表現形式見圖4，不平衡力一周期為0.03 s，可知與轉子的轉速是吻合的。由圖4結合式(2)可獲得不平衡量在實驗臺圓盤30 mm半徑處，質量為 1.232 1 g，相位為46.035 2°。

利用上述識別的不平衡量對實驗臺進行動平衡處理，對完成動平衡以后的實驗臺測試瞬態響應來評價動平衡效果。在主軸圓盤30 mm半徑處，加一大小與識別的不平衡量質量相同，施加的角度方向與識別出的相位角方向相反。即由識別出的相位角上減去180°或者加上180°獲得不平衡質量施加的角度，類似于在動平衡圓盤上施加一個與識別不平衡量大小相等，方向相反的力。運行施加了不平衡量的轉子實驗臺，測試其瞬態響應，并進行配重前后瞬態響應對比。將測得的瞬態響應與動平衡前進行比較。從圖5和表2可知，測點在動平衡前后的振動幅度有了很大的下降，從而動平衡的效果比較好。

圖4　轉子實驗臺上的識別的不平衡力Fig.4　The identified unbalance forces of the test rig

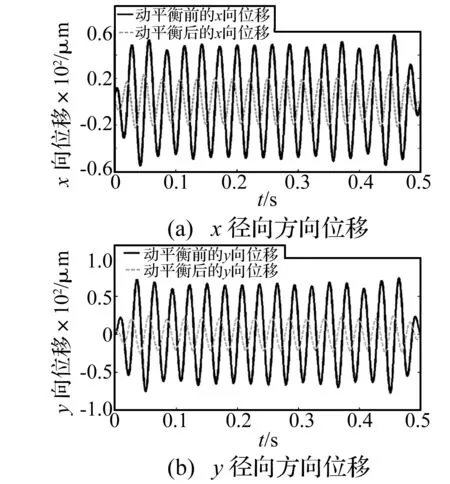
圖5　兩測點動平衡前后的瞬態響應比較Fig.5　Experimental unbalance responses: before and after the balancing procedure

表2　動平衡前后的振幅結果比較

3.3考慮不確定變量的實驗臺不平衡量識別

前面實驗臺中識別不平衡量是假設滑動軸承油膜特性系數是一固定值，與不平衡量的大小無關，而實際上不平衡量的大小影響作用在軸頸處的力的大小，而此力影響滑動軸承油膜特性系數。本節考慮滑動軸承油膜特性系數為不確定變量時對不平衡量識別結果的影響。

滑動軸承油膜剛度系數kyx,阻尼系數cxx,cxy,cyx因不平衡量幅值的變化而變化，受不平衡量的影響較大，故選定前軸承油膜剛度系數kyx,阻尼系數cxx,cxy,cyx為不確定變量。其中點值和5%的不確定性水平下的區間見表3。不平衡量對應不確定變量kyx,cxx,cxy,cyx的一階偏導數通過確定性不平衡量識別方法和中心差分有限元方法獲得，圖6～圖9顯示其對應的敏感度關系曲線，由圖可知不平衡量對于kyx,cxx,cxy,cyx都比較敏感。

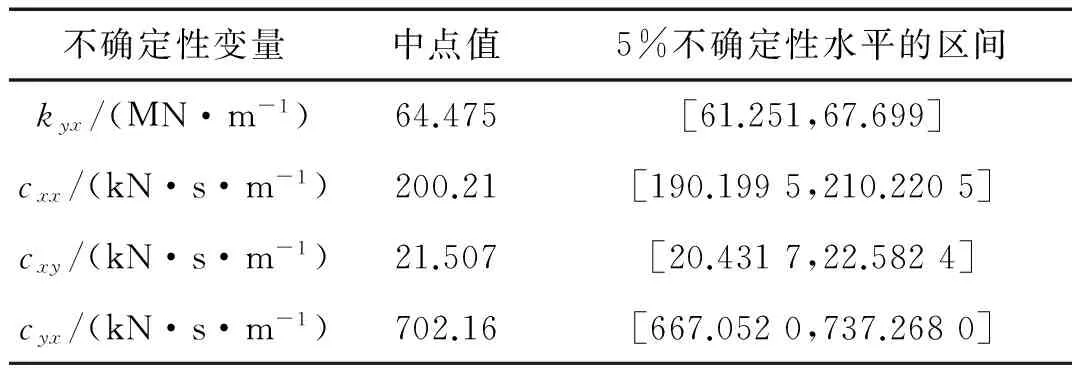
表3　不確定變量的中點和區間

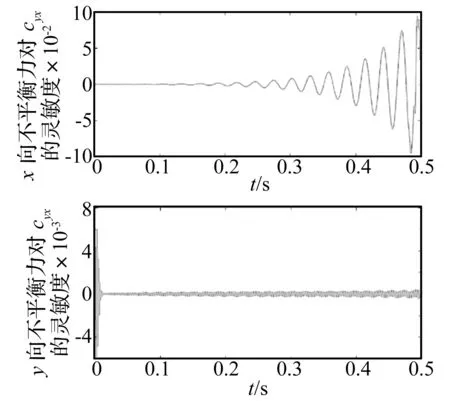
圖6　不平衡力關于剛度系數kyx的敏感度曲線Fig.6　The sensitivity curve of the unbalance force to stiffness coefficient kyx

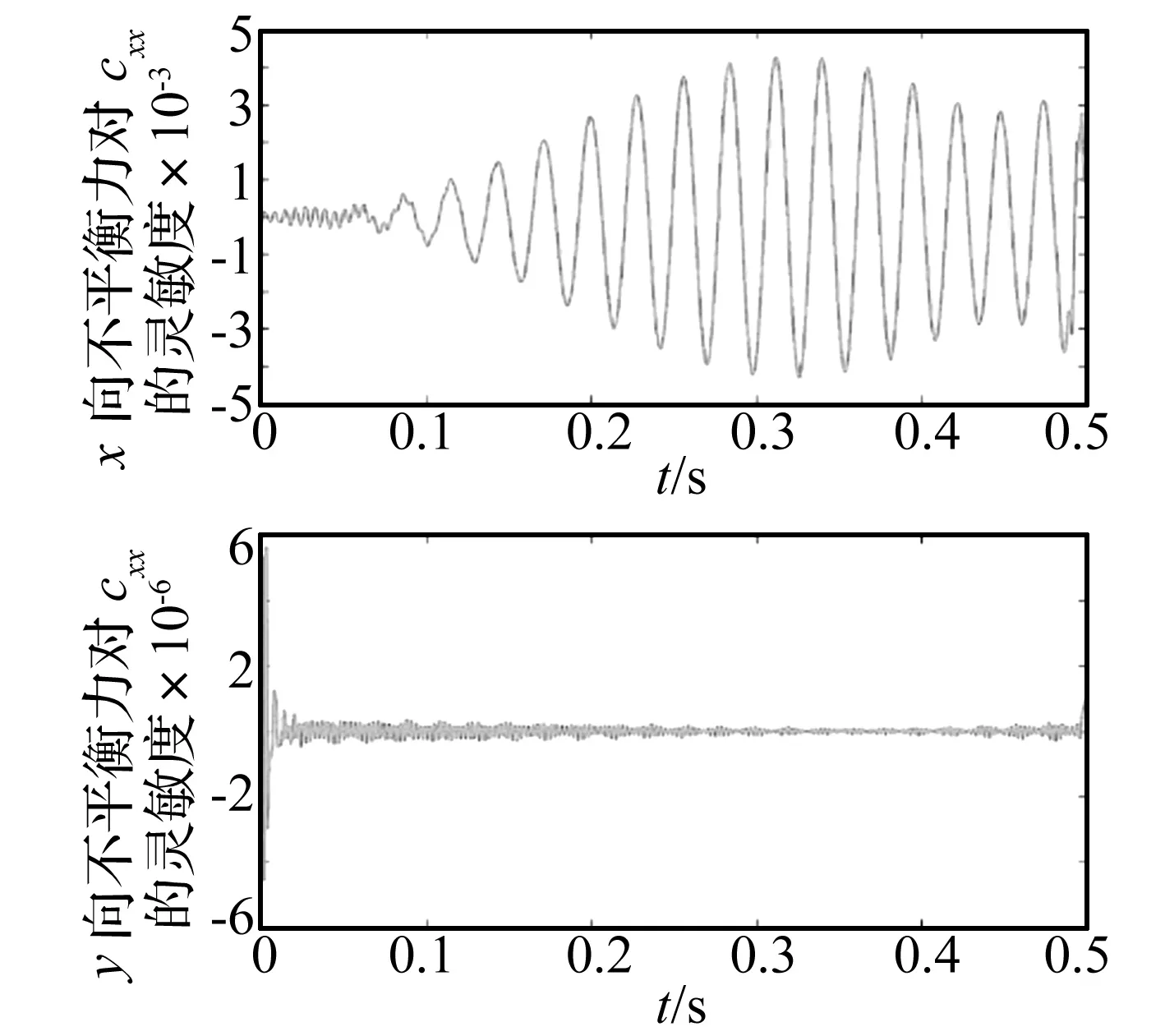
圖7　不平衡力關于阻尼系數cxx的敏感度曲線Fig.7　The sensitivity curve of the unbalance force to damping coefficient cxx

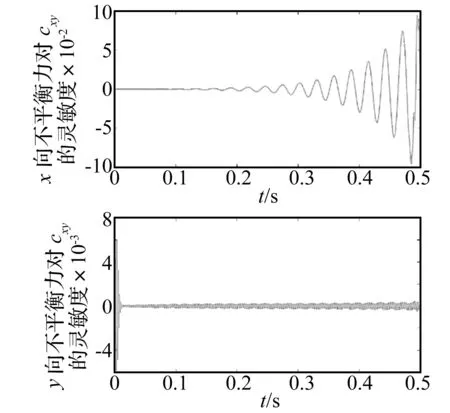
圖8　不平衡力關于阻尼系數cyx的敏感度曲線Fig.8　The sensitivity curve of the unbalance force to damping coefficient cyx

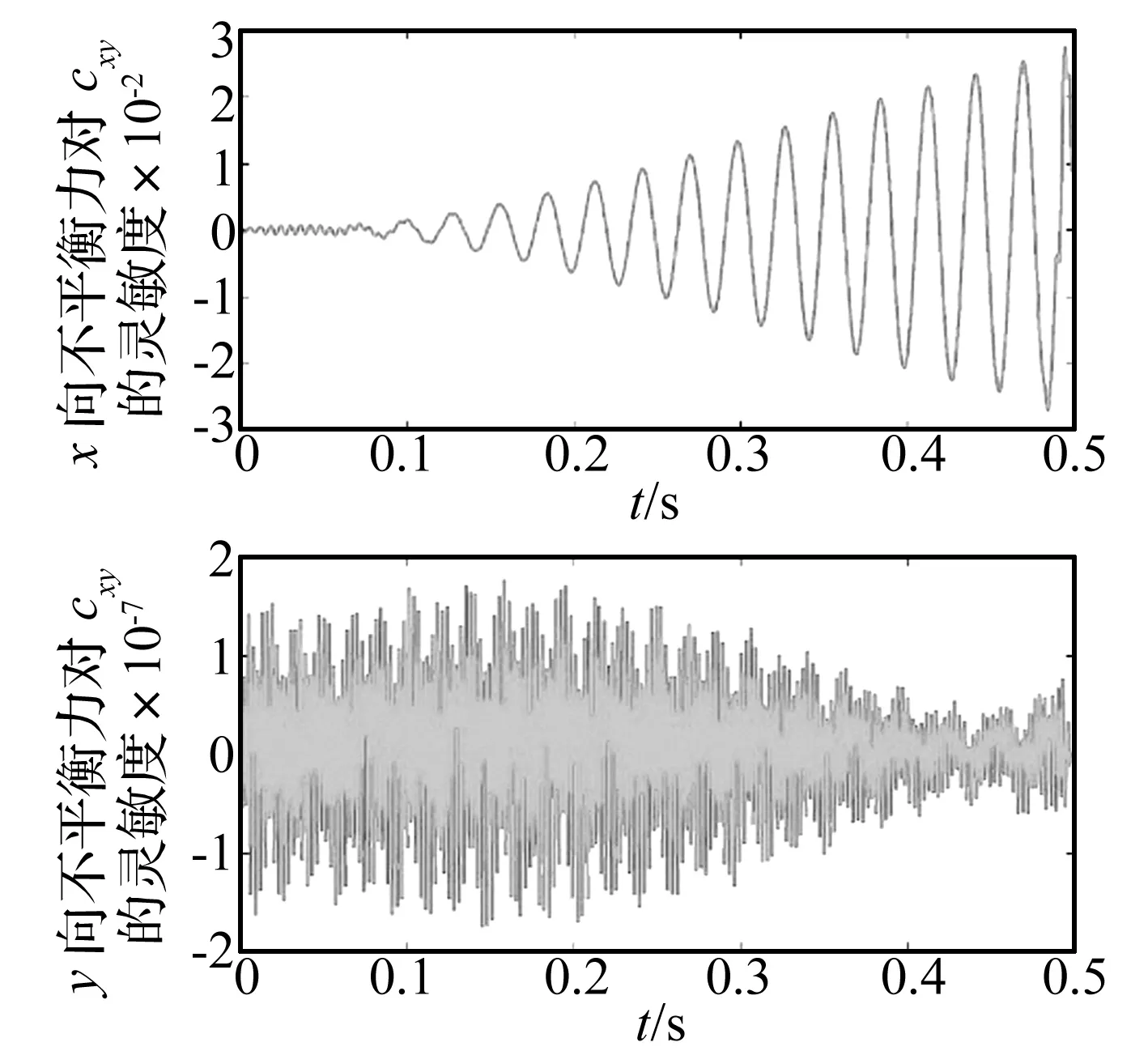
圖9　不平衡力關于阻尼系數cxy的敏感度曲線Fig. 9 The sensitivity curve of the unbalance force to damping coefficient cxy

利用不平衡量識別不確定性變量中點處的不平衡量、敏感度曲線和式(14)和式(15)，采用區間法計算可得到不平衡量在5%不確定性水平下的上下邊界，如圖10所示，圖10中顯示不確定變量對滑動軸承-轉子系統兩徑向方向x，y的瞬態響應，由圖10可知不確定變量對x向的不平衡量影響較大。

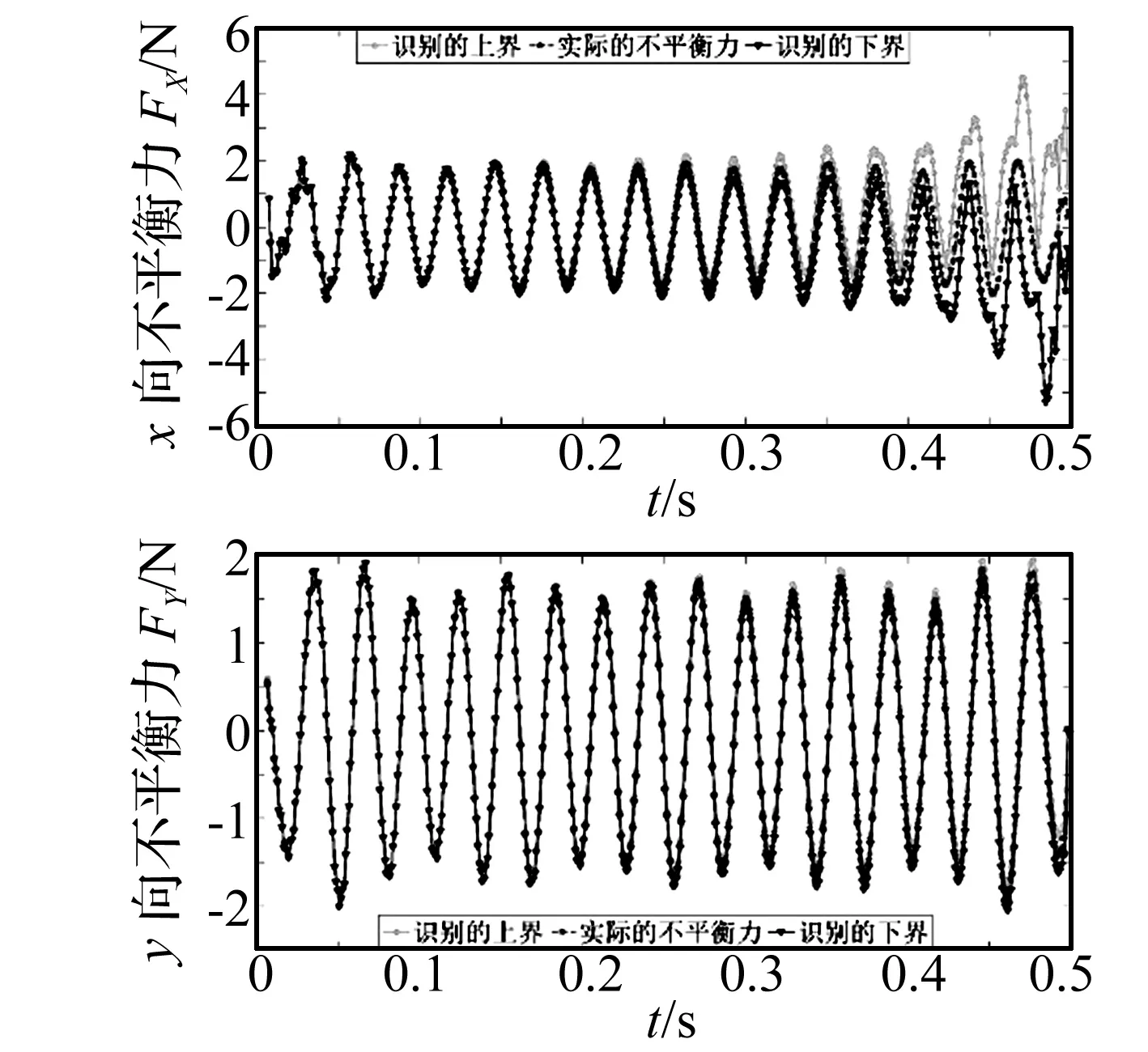
圖10　5%不確定性下不平衡力識別的邊界Fig.10　The bounds of the identified unbalance force at 5% uncertainty level

考慮滑動軸承油膜特性系數受不平衡量的大小的影響，基于不確定變量的不平衡量識別獲得滑動軸承-轉子系統的不平衡量的區間如表4。當滑動軸承油膜特性系數在一定范圍變化時，識別的不平衡量也在一定范圍里變化。當缺少滑動軸承-轉子系統樣本和滑動軸承油膜特性系數統計數據時,使用區間分析方法進行滑動軸承-轉子系統的不平衡量分析是較為準確的，是十分必要的。

表4　基于區間方法的實驗臺不平衡量識別結果

4　結　論

本文提出一種滑動軸承-轉子系統中不平衡量識別的方法。針對實際的滑動軸承-轉子系統中，在不平衡量識別過程中，滑動軸承油膜特性系數的取值對不平衡量的識別結果是有影響的。取滑動軸承的剛度系數kyx,阻尼系數cxx,cxy,cyx這四個值作為不確定變量，基于區間方法提出一種基于區間的不確定變量的不平衡量識別方法。基于一階泰勒級數展開式的區間法將具有不確定變量的結構的不平衡量識別方法轉化為兩類確定變量的不平衡量識別問題，并通過正則化方法處理不平衡量識別中的病態問題，從而獲得滑動軸承-轉子系統不平衡量的上下邊界。最后運用本文方法獲得轉子實驗臺的不平衡量，動平衡轉子實驗臺，比較動平衡前后的位移幅值大小來檢驗此方法的有效性。

[1] 劉淑蓮,李強,鄭水英.基于全息譜分析的非線性轉子系統不平衡量識別[J].機械工程學報,2010,46(17)：62-67.

LIU Shulian,LI Qiang,ZHENG Shuiying.Unbalance Identifi-cation of nonlinear rotor system based on holospectrum analysis[J].Journal of Mechanical Engineering,2010,46(17):62-67.

[2] QUEIROZ M S.An active identification method of rotor unbalances parameters[J].Journal of Vibration and Acoustics-Transactions of the ASME, 2009, 15(9):1365-1374.

[3] DHAKAR G N D S,SEKHAR A S.Identification of unbalance in a rotor bearing system[J].Journal of Sound and Vibration, 2011,330:2299-2313.

[4] VILLAFANE SALDARRIAGA M, STEFFEN JR V, DER HAGOPIAN J, et al. On the balancing of flexible rotating machines by using an inverse problem approach[J].Journal of Vibration and Control, 2011, (17): 1021-1033.

[5] TIWARI R,CHAKRAVARTHY V. Simultaneous identification of residual unbalances and bearing dynamic parameters from impulse responses of rotor-bearing systems[J].Mechanical Systems and Signal Processing, 2006, 20(7):1590-1614.

[6] LIU Shulian,LI Qiang,ZHENG Shuiying,et al.Unbalance identification of nonlinear rotor system based on holospectrum analysis[J].Journal of Mechanical Engineering, 2010,146(17):62-67.

[7] DING Y, ZHAO B Y, WU B, et al. A condition assessment method for time-variant structures with incomplete measure ments[J].Mechanical Systems and Signal Processing, 2015, 58/59:228-244.

[8] LU Z R, LAW S S. Identification of prestress force frommeasured structural responses [J]. Mechanical Systems and Signal Processing, 2006, 20(8): 2186-2199.

[9] CASTRO H F,CAVALCA K L,CAMARGO L W F, et al. Identification of unbalance forces by metaheuristic search algorithms [J]. Mechanical Systems and Signal Processing, 2010,24(6):1785-1798.

[10] GAGNOL V,LE T P, RAY P.Modal identification of spindle-tool unit in high-speed machining[J]. Mechanical Systems and Signal Processing, 2011,25(7): 2388-2398.

[11] 姜潮.基于區間的不確定性優化理論與算法[D].長沙:湖南大學,2008.

[12] 毛文貴,韓旭,劉桂萍. 基于流固耦合的滑動軸承非線性油膜動特性研究[J].中國機械工程,2014,25(3):383-387.

MAO Wengui, HAN Xu,LIU Guiping. Research on dynamic character of sliding bearing nonlinear oil-film based on fluid-structure interaction [J]. China Mechanical Engineering, 2014,25(3):383-387.

[13] 王軍,洪杰,陳萌,等.航空發動機轉子系統動力特性的非概率分析[J].航空動力學報,2012, 27(1):75-81.

WANG Jun,HONG Jie,CHEN Meng,et al. Non-probabilistic analysis on aero-engine rotordynamics [J].Journal of Aerospace Power, 2012, 27(1):75-81.

[14] 郝勇,陳萌,洪杰,等.基于泰勒展開法的轉子系統動力特性區間分析方法[J].航空動力學報,2014,29(3):571-577.

HAO Yong，CHEN Meng，HONG Jie, et al. Interval analysis method of rotordynamics based on Taylor expansion method[J].Journal of Aerospace Power, 2014, 29(3):571-577.

[15] 王曉軍,楊海峰, 邱志平,等.基于Green函數的動態載荷區間識別方法研究[J]. 固體力學學報,2011,32(1):95-101.

WANG Xiaojun,YANG Haifeng,QIU Zhiping, et al.Research on interval identification method for dynamic loads based on Green’s function[J]. Chinese Journal of Solid Mechanics, 2011, 32(1):95-101.

[16] LIU J, SUN X S, HAN X, et al.Dynamic load identi-fication for stochastic structures based on Gegenbauer polyno-mial approximation and regularization method[J]. Mechanical Systems and Signal Processing, 2015,56/57:35-54.

[17] 劉淑蓮,鄭水英.應用遺傳算法的非線性轉子-軸承系統參數辨識[J].動力工程，2006,26(4):479-534.

LIU Shulian，ZHENG Shuiying. Parameter identification of rotor-bearing systems with non-linear behavior by using genetic algorithm[J]. Journal of Power Engineering,2006, 26(4):479-534.

[18] SHIH Y P, LEE A C.Identification of the unbalance distribution in flexible rotors [J]. Int J Mech Sci,1997,39(7):841-857.

[19] 劉杰.動態載荷識別的計算反求技術研究[D].長沙:湖南大學,2011.

[20] YANG X J, WANG L. A modified Tikhonov regularization method [J]. Journal of Computational and Applied Math-ematics, 2015, 288:180-192.

[21] MOLABAHRAMI A.An algorithm based on the regulari-zation and integral mean value methods for the Fredholm integ-ral equations of the first kind [J]. Applied Mathematical Mod-elling, 2013, 37:9634-9642.

[22] 劉繼軍.不適定問題的正則化方法及應用[M].北京:科學出版社, 2005.

[23] SUN X S, LIU J, HAN X, et al.A new improved re-gularization method for dynamic load identification[J].Inverse Problems in Science and Engineering,2014, 22(7): 1062-1076.

[24] 韓波,李莉.非線性不適定問題的求解方法及其應用[M].北京:科學出版社, 2011.

Unbalance parameters identification for a sliding bearing-rotor system considering the uncertainty of parameters

MAO Wengui1,2, LI Jianhua1, LIU Guiping2, LI Jie2

(1. Hunan Province Cooperative Innovation Center for Wind Power Equipment and Energy Conversion, College of Mechanical Engineering, Hunan Institute of Engineering, Xiangtan 411101, China;2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)

An identification method considering the uncertainty of the dynamic parameters of bearings in a sliding bearing-rotor system was presented to identify the unbalance parameters of the system. In the method, the unbalance parameters identification was transformed into two deterministic inverse problems by using the interval analysis with the first order Taylor series expansion. Then, the unbalance forces, used as the unblance parameters, were expressed as a series of impulse functions in time domain and the discretized convolution integral of unbalance forces and the corresponding transient response functions of the sliding bearing-rotor system were adopted to construct a forward model. A regularization method was introduced to deal with the ill-posedness arising from the deconvolution and noisy responses, and then the upper and lower bounds of the unbalance parameters were easily obtained through the interval expanding operation. The efficiency and robustness of the proposed method were verified on a test rig.

sliding bearing-rotor systems; unbalance parameters identification; uncertainty; bearing dynamic parameters; interval analysis

高等學校博士學科點專項科研基金(20130161130001); 湖南省自然科學基金資助項目(2016JJ6026 )；湖南省教育廳資助科研項目(15B057);常州市科技支撐計劃(CE20140027)

2015-10-20修改稿收到日期：2016-05-09

毛文貴 女，博士，副教授，1975年生

TH113.1;O322

A DOI:10.13465/j.cnki.jvs.2016.18.035