狹長空間基于人體穿透損耗模型的組合定位方法

張晉升，孫　健，李勝廣，譚　林

（公安部第一研究所，公安部警務物聯網應用技術重點實驗室，北京100048）

狹長空間基于人體穿透損耗模型的組合定位方法

張晉升*，孫健，李勝廣，譚林

（公安部第一研究所，公安部警務物聯網應用技術重點實驗室，北京100048）

狹長空間定位問題普遍存在于室內定位應用場景中，雖然傳統基于RSSI（Received Signal Strength Indicator）測距的定位方法簡便易行，但是狹長空間RSS的波動性以及人體對無線信號的遮擋會嚴重降低人員定位精度。本文在分析了人體穿透損耗對狹長空間定位影響的基礎上，提出將RSSI測距與擴展卡爾曼濾波定位算法組合實現定位，即在中等尺度（5λ～50λ）內采用基于人體穿透損耗模型的RSSI測距方法定位，在大尺度（＞50λ）內采用基于人體遮擋修正模型的擴展卡爾曼濾波算法定位。實驗表明該方法在狹長空間的定位精度明顯優于RSSI測距定位方法。

狹長空間；人體穿透損耗；RSSI測距；組合定位

EEACC:7230doi:10.3969/j.issn.1004-1699.2016.04.022

位置服務LBS（Location Based Services）發展十分迅速，可以與社交、旅游、商業等行業緊密結合，產生巨大的商業價值［1］。室內定位是位置服務中非常重要的組成部分，尤其是狹長空間定位問題，場景特殊，信號多徑效應以及遮擋、串擾等干擾嚴重，但是普遍存在，例如礦井通道內的人員定位，監管場所、機場、大型醫院的走廊內人員定位等等。

國內遼寧工業大學的趙光旭研究了監獄服刑人員三維精確定位系統［2］；陳增強研究了基于模糊神經網絡建模的室內定位算法［3］；上海交通大學的李成嶺研究了基于RSSI的無線自組織網絡室內定位算法研究與實現［4］；黃應紅研究了基于改進接收信號強度指示的室內定位算法，通過神經網絡對權值進行擬合［5］；楊小亮研究了基于閾值分類及信號強度加權的室內定位算法，減小RSSI隨機抖動引起的誤差［6］。此外，還有研究指紋定位算法［7］、加權質心算法［8］、二次相關算法［9］、貝葉斯算法［10］、聚類算法［11］、卡爾曼濾波定位算法［12］、粒子濾波定位算法［13］等等。

目前室內定位相關的研究對于人體遮擋損耗的關注較少，相關算法較少涉及人體穿戴對信號傳播的影響，使得這些方法在實驗室內的定位精度較高，但是在實際應用中無法達到理想的定位精度。本文針對狹長空間RSS的波動性以及人體對無線信號的遮擋會嚴重，進而降低人員定位精度的問題作了研究。提出了將RSSI測距與粒子濾波定位算法組合實現定位，即在中等尺度（5λ～50λ）距離范圍采用基于人體穿透損耗模型的RSSI測距定位方法，在大尺度（＞50λ）距離范圍采用基于人體遮擋修正模型的擴展卡爾曼濾波組合定位算法。

1　人體穿透損耗分析

在眾多室內定位的算法中，基于信號強度衰減的方法更適合于狹長空間內人員定位［14］。對于經典的信號衰減模型，收發功率的關系由式（1）表示。

式中，Pr為接收信號的功率，Pt為發射信號的功率，d為接收節點與發射節點之間的距離，n為與無線網絡環境有關的傳播因子或傳播系數。

簡化模型為:

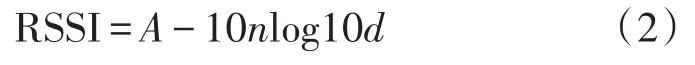
式中，RSSI為節點接收到的信號強度，A為節點之間間距為1 m時，接收到的信號的平均能量，單位為dBm，n為環境傳播因子，受外界環境影響較大，反映了信號能量隨距離增大的衰減速率。根據式（2）可得節點之間的距離計算公式為:

根據式（3）以及測得的RSSI值可以推算得到距離值，但是對于狹長空間測得誤差值較大，且RSSI值波動較大，圖1為狹長空間正對錨節點時測得RSSI值以及根據式（2）得到的曲線，可以看出兩曲線在＞5 m的范圍（即在大尺度（＞50λ））吻合度非常低，由此可知如果利用式（3）得到距離值誤差較大，而在＜5 m的范圍（即在中等尺度（5λ～50λ））實際曲線與理想擬合曲線吻合度較高。

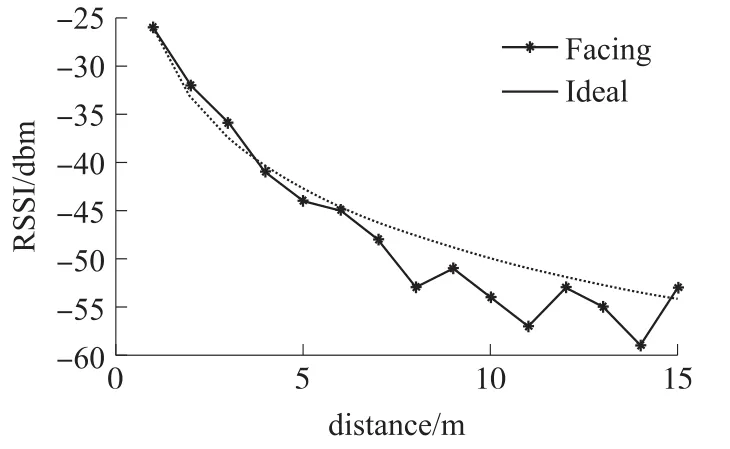
圖1　狹長空間RSSI值變化與理想環境下對比圖

圖1中面對錨節點的RSSI測量從1 m～15 m，測量點間隔為1 m，每個測量點重復20次測量取平均值作為測得RSSI值。理想環境下曲線的繪制中，取1 m衰減系數A=126 dBm，環境因子n=2.4。

雖然人體的遮擋面積遠小于墻壁，但是由于對人體進行定位的便攜式設備通常掛在人體的腰部、腕部、胸部等位置，人體對電磁波的傳播損耗衰減能力不亞于墻壁。因為當人體戴有便攜式設備的一側正對定位錨節點時，便攜式設備與定位錨節點之間的電磁波傳播是視距傳播；當戴有便攜式設備的一側背對定位錨節點時，它們之間的電磁波傳播是非視距傳播，此時人體的穿透損耗非常嚴重，如果在定位過程中不考慮這個因素，仍然使用經驗電磁波衰減損耗模型來計算距離進行定位，導致定位誤差變大。

當人體戴有便攜式設備的一側正對定位錨節點時，電磁波信號強度衰減隨距離遠近的變化趨勢如圖2中*曲線所示；當戴有便攜式設備的一側背對定位錨節點時，電磁波信號強度衰減隨距離遠近的變化趨勢如下圖2中+曲線所示。

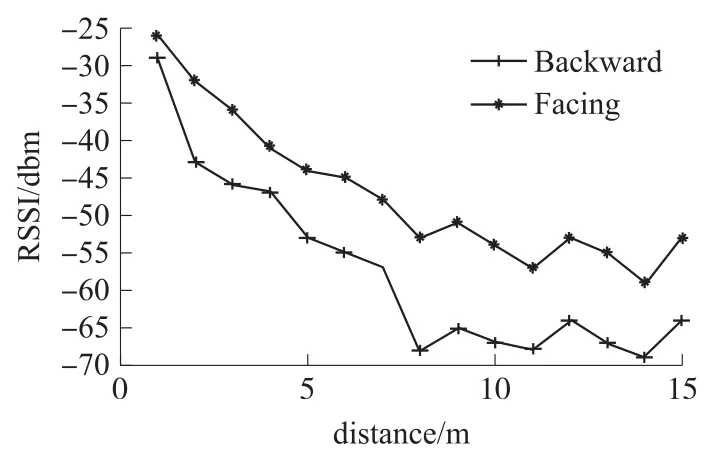
圖2　正、背對錨節點電磁波信號強度衰減隨距離遠近的變化趨勢對比圖

從圖2可知RSSI值不僅受環境因素的影響，在上述實驗過程中RSSI的值受人體遮擋平均衰減強度在10 dBm，說明人體在攜帶設備的過程中身體的遮擋會嚴重影響非視距一側的RSSI值測量。

理論分析和實驗驗證均表明，受狹長空間周圍介電系數，兩壁環境的反射系數，無線電磁波的傳導效應等多種因素影響，添加補償因子b和c對式（3）進行修正，才可應用到狹長空間，為此得到應用于狹長空間的RSSI測距計算公式:

當人體戴有便攜式設備的一側正對定位錨節點時，人與正對錨節點之間的距離為:

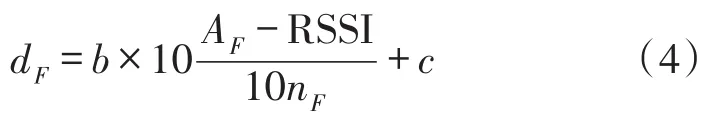
式中，AF為人正對錨節點時測得1 m接收信號的平均能量，nF為人正對錨節點時的環境因子；

當戴有便攜式設備的一側背對定位錨節點時，人與背對錨節點之間的距離為:

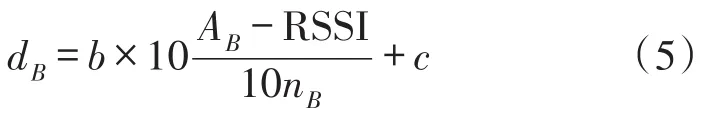
式中，AB為人背對錨節點時測得1 m接收信號的平均能量，nB為人背對錨節點時的環境因子。

當得到修正后的距離結果后，不管是通過三邊法、三角法、加權質心法還是指紋定位算法來計算未知節點的坐標，都可以在很大程度上減小定位誤差。由于狹長空間的獨特性（寬度在2 m～3 m），甚至不要求得縱向坐標，即只需要得知目標在狹長空間內的橫坐標，通過以上方法求得的距離值和錨節點的坐標相加減即可方便求得未知節點的位置，不但繼承了RSSI測距定位的簡潔性，同時提高定位精度。

為了減小環境因素的影響，同時利用正對錨節點和背對錨節點測得的修正值來對目標做定位，進一步提高定位精度。根據正對與背對錨節點的修正距離值采用加權平均算法得到定位結果:

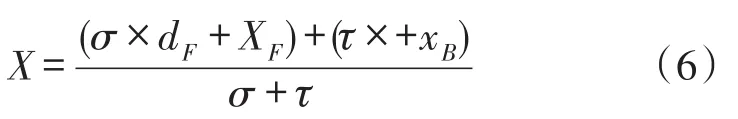
式中，σ、t分別為正、背對錨節點的加權系數，dF、dB分別為測得正、背對錨節點的修正后的距離值，XF、XB分別為正、背對錨節點的實際坐標位置。

2　組合定位方法

在分析了人體穿透損耗對狹長空間定位影響的基礎上，提出將RSSI測距與擴展卡爾曼濾波定位算法組合實現定位，即在中等尺度（5λ～50λ）內采用基于人體穿透損耗模型的RSSI測距定位方法，在大尺度（＞50λ）內采用基于人體遮擋修正模型的擴展卡爾曼濾波定位算法。

在在中等尺度（5λ～50λ）內采用基于人體穿透損耗模型的RSSI測距定位方法，其原因是在中等尺度內RSSI測距受外界的干擾較小。首先，RSSI在中等尺度閾值內時，節點之間一般不存在障礙物，電磁波的傳播是視距傳播；其次，RSSI在中等尺度閾值內時，其信號強度較強、信號質量穩定、較少經過墻面的反射、折射等，信號傳播以直達波為主；所以，在中等尺度閾值內采用基于人體穿透損耗模型的RSSI測距定位方法精度高，并且可以避免系統不停進行迭代計算，進而減小系統的計算復雜度。

在大尺度（＞50λ）距離范圍采用基于人體遮擋修正模型的擴展卡爾曼濾波定位算法，EKF方法基于遞歸最小均方的估計方法，可用于處理非線性系統，經常用于目標跟蹤定位中，而且該方法在抑制多途效應影響方面具有較好的性能。

選用基于人體穿透損耗模型的RSSI測距定位結果作為擴展卡爾曼濾波的初始值，相對于均值初始化更加精確，同時可以減少迭代次數。

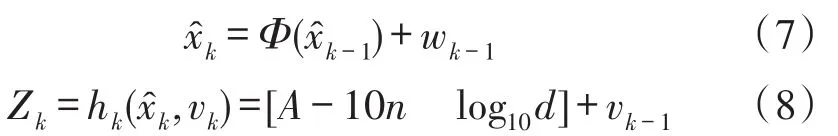
可以詳細寫為:

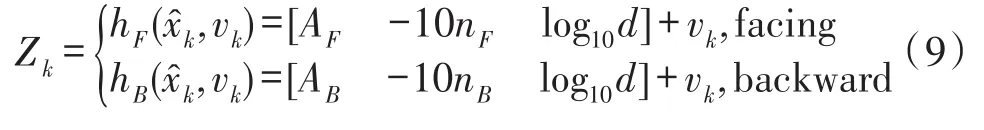
式中，hk（·）為非線性觀測方程。假設過程激勵噪聲wk-1和觀測噪聲vk-1均為高斯白噪聲，協方差分別為Q、R。

設RSSi為定位節點收到的第i個錨節點的RSS值，可得k時刻的觀測向量為:

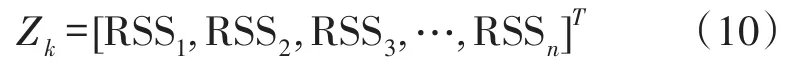
由于便攜式定位節點與錨節點通常不在同一水平面，為了減小定位誤差需要考慮它們之間的高度差，d為錨節點與便攜式設備之間的距離:

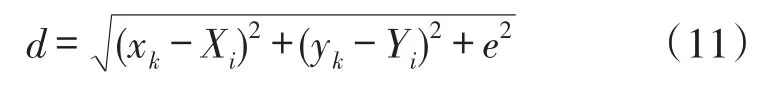
式中，［Xi，Yi］為第i個錨節點的坐標值，e為便攜式定位節點距離安裝的錨節點的垂直方向的高度差，如圖3所示。

圖3　組合定位局部示意

更新狀態xk的協方差矩陣:

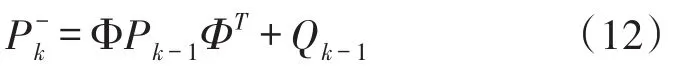
Kalman增益矩陣Kk通過Zk計算，然后利用測量結果估計出當前目標位置:

其中Hk為在由k-1時刻向k時刻轉換時，對xk求導數，即，可得雅可比矩陣為:

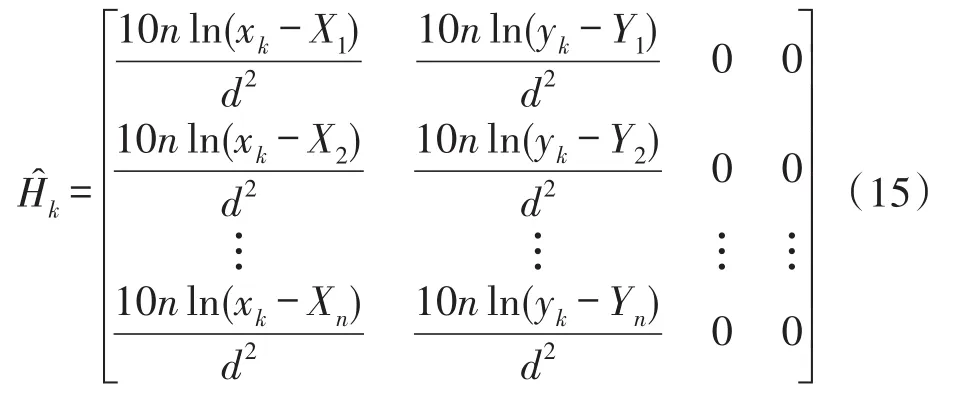
這里的n包含了nF和nB，分別對應正對的錨節點和背對的錨節點。

用于更新狀態估計的狀態協方差Pk，如下式:

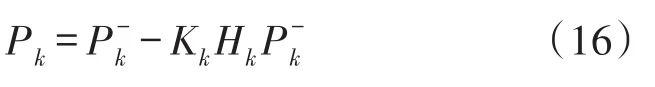
通過測量更新方程進行計算求得坐標結果。

3　實驗驗證與分析

為了驗證本實驗方法的有效性，在L型狹長樓道搭建了實驗系統如圖4所示，狹長型樓道的寬度為2 m，長度為75 m+50 m，系統中錨節點安裝在頂部中線位置，便攜式目標節點位于人體腰部，距離頂部的垂直距離約為2 m。對于狹長空間的人員定位，由于空間寬度較窄，一般在2 m～3 m之間，在該方向上的最大定位誤差在1 m左右，可以通過加裝錨節點來實現該方向的高精度定位，但是沒有實際應用的意義，所以對于狹長空間一般采用相隔固定距離單獨安裝一個錨節點的方式，來降低工程成本增加節點布置實用性。所以本實驗采用相隔20 m安裝一個定位錨節點的方式進行實時定位。

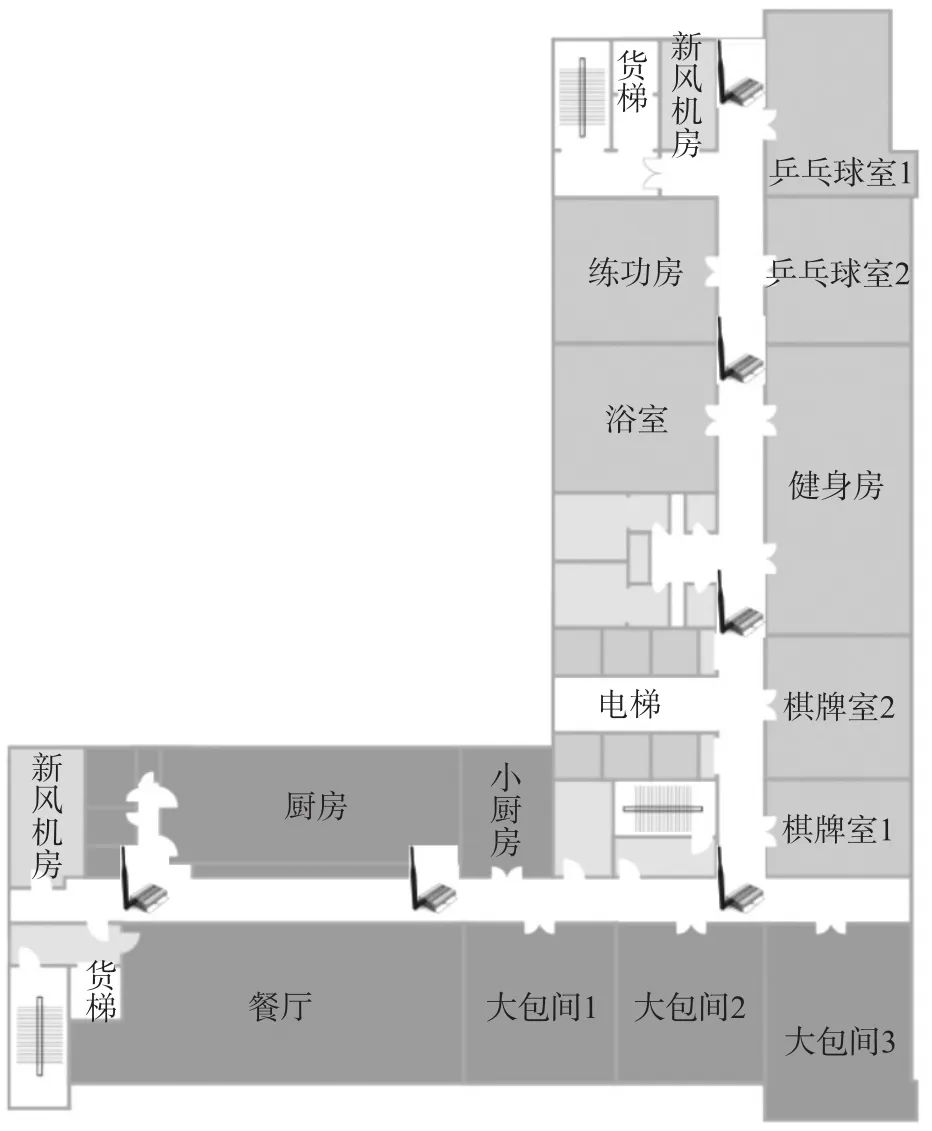
圖4　狹長樓道實驗環境示意圖

目標節點在移動過程中與錨節點之間通信，測得相應的RSSI值，通過無線網絡傳輸至后臺服務器，服務器對目標進行定位解算。為了取得較好的實時性，目標節點與錨節點之間每隔1 s進行一次通信進行數據上報。

與開闊空間的人員定位不同，對于狹長空間的人員定位在寬度方向的定位意義不大，實際應用中最重要的是長度方向的定位。因此本文僅對水平方向也就是橫坐標定位誤差進行分析。

為了說明本文實驗方法的有效性，分別做了以下4種對比定位實驗:

①正對錨節點測距實驗。理想環境曲線的繪制中，取1 m衰減系數A=126 dBm，環境因子n=2.4。

表1　正對錨節點測距實驗結果對比

②背對錨節點測距實驗。理想環境曲線的繪制中，取1 m衰減系數A=129 dBm，環境因子n=3.4。

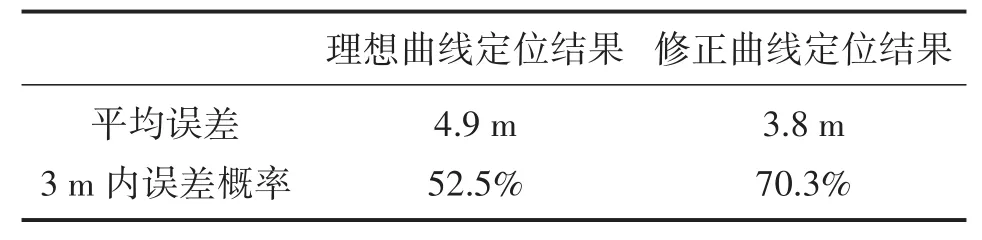
表2　背對錨節點測距實驗結果對比

③聯合正、背對錨節點加權平均修正定位實驗。理想環境曲線的繪制中，取1 m衰減系數A= 128 dBm，環境因子n=3.0。

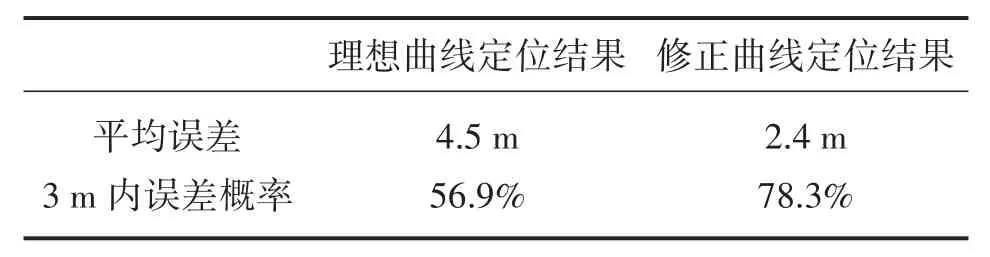
表3　聯合正、背對錨節點加權平均修正定位實驗結果對比

④組合定位實驗。

組合定位解算的過程可以分為定位初始化和一般定位過程。定位初始化過程分兩步:首先，通過收集到的各錨節點的RSSI值來判斷目標節點處于錨節點的中等尺度或者大尺度距離范圍內；其次，如果目標節點處于錨節點的中等尺度距離范圍內，選出距離最近的錨節點，采用該錨節點測得RSSI值來作基于人體損耗模型的距離推算并且定位；如果目標節點處于錨節點的大尺度距離范圍內，則采用基于人體損耗模型的卡爾曼濾波算法進行定位，此時的迭代初值選用均值。在一般定位過程中，當目標節點進入錨節點的中等距離范圍時自動切換為基于人體損耗模型的距離推算模式，當目標節點進入大尺度距離范圍時自動切換為改進的卡爾曼濾波方式，初值采用模式切換前的定位結果。

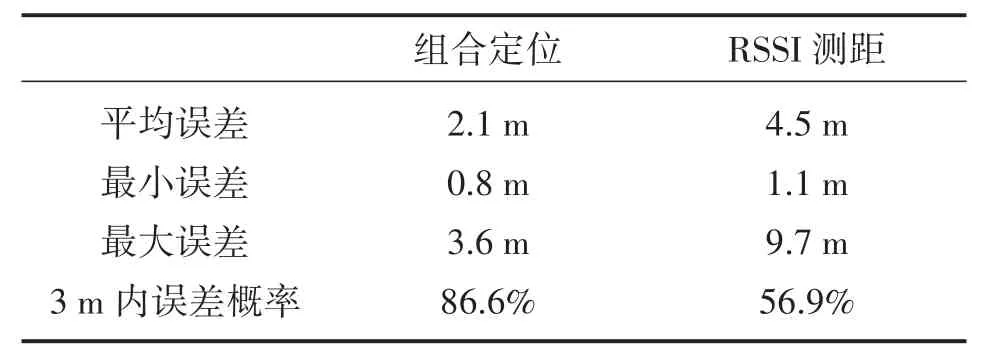
表4　基于人體穿透損耗組合定位和RSSI測距定位均方根誤差對比

從文獻［15］可知，在不同環境參數下的誤差曲線均表明誤差會隨著測距距離的增加而增大，1 m～3 m范圍內最大測距誤差為1.07 m，3 m～5 m范圍內最大測距誤差為1.62 m，5 m～7 m范圍內最大測距誤差為4.34 m。在實驗環境下5 m范圍內的誤差呈現緩慢增加的趨勢，但當通信距離超過5 m時誤差開始明顯增大，在有噪聲干擾的情況下5 m內的誤差也明顯增大。

本文所述組合定位算法不僅經過實驗環境測試，同時還應用在江蘇省興化市看守所的警員安全警戒系統中，在實際應用中驗證了該定位算法的有效性。

實際的定位環境中狹長樓道數量眾多，狹長型樓道的寬度為2 m，長度為50 m～100 m不等，系統中錨節點安裝在頂部中線位置，相隔20 m安裝一個定位錨節點的方式進行實時定位，便攜式目標節點位于人體腰部，距離頂部的垂直距離約為2 m，定位誤差在3 m內的概率不低于80%，定位實時性較好，延時不低于3 s。

4　結論

本文針對狹長空間RSS的波動性以及人體對無線信號的遮擋會嚴重，進而降低人員定位精度的問題作了研究并且做了大量對比實驗。提出了將RSSI測距與粒子濾波定位算法組合實現定位，同時修正了因人體遮擋帶來的信號衰減。實驗表明，該方法錨節點部署方法簡便，實用性強，并且相對于傳統的RSSI測距定位方法，該方法定位精度高，相對于單純采用卡爾曼濾波算法進行定位的實時性好。

［1］ 劉成.LBS定位技術研究與發展現狀［J］.導航定位學報，2013（1）:78-83.

［2］ 趙光旭.監獄服刑人員三維精確定位系統研究與設計［D］.遼寧工業大學，2014.

［3］ 陳增強，國峰，張青.基于模糊神經網絡建模的RFID室內定位算法［J］.系統科學與數學，2014，34（12）:1438-1450.

［4］ 李成嶺.基于RSSI的無線自組織網絡室內定位算法研究與實現［D］.上海:上海交通大學，2012.

［5］ 黃應紅.基于改進接收信號強度指示的室內定位算法［J］.激光雜志，2014（12）:144-147.

［6］ 楊小亮，葉阿勇，凌遠景.基于閾值分類及信號強度加權的室內定位算法［J］.計算機應用，2013，33（10）:2711-2714.

［7］ Areekul V，Boonchaiseree N.Fast Focal Point Localization Algorithm for Finger Print Registration［J］.IEEE Conferenceon Industrial Electronics&Applications，2008（3）:2089-2094.

［8］ 劉運杰，金明錄，崔承毅.基于RSSI的無線傳感器網絡修正加權質心定位算法［J］.傳感技術學報，2010，23（5）:717-721.

［9］ 張晉升，李一博，王偉魁，等.基于TFDA的有限空間多目標聲定位方法［J］.傳感技術學報，2013，26（11）:1508-1512.

［10］JosuéIglesias，Ana M Bernardos，José R Casar，et al.ABayesian Strategy to Enhance the Performance of Indoor Localizati on Systems［J］.Advancesin Intelligent&Soft Computing，2011.

［11］Suroso D J，Cherntanomwong P，Sooraksa P，et al.Finger Print-Based Technique for Indoor Localization in Wireless Sensor Networks Using Fuzzy C-Meansclusteringalgorithm［C］//Intelligent Signal Processing and Communications Systems（ISPACS），2011 International Symposiumon IEEE，2011，1-5.

［12］Paul A S，Wan E.RSSI-Based Indoor Localization and Tracking Using Sigma-Point Kalman Smoothers［J］.IEEEJournal of Selected Topicsin Signal Processing，2009，3（5）:860-873.

［13］Widyawan，Klepal M，Beauregard S.A Novel Back Tracking Particle Filter for Pattern Matching Indoor Localization［J］.Melt'08 Proceeding Sof the First Acm International Workshop on Mobile，2008（9）:79-84.

［14］王巍強.基于電力線位置指紋定位系統構造技術研究［D］.北京:北京工業大學，2013.

［15］張蒼松.基于RSSI的室內定位算法優化技術［D］.西北大學，2014.

張晉升（1988-），男，山西大同人，公安部第一研究所二級警司。主要研究方向為室內定位技術和警用可穿戴技術，zjsgab@163.com；

孫健（1983-），男，博士，河北人，公安部第一研究所三級警督。主要研究方向為室內定位技術和嵌入式技術研究，shijsunbj@139.com。

Combination Positioning Method for Long and Narrow Space Based on the Human Body Penetration Loss Model

ZHANG Jinsheng*，SUN Jian，LI Shengguang，TAN Lin
（First Research Institute of the Ministry of Public Security of PRC，Key Laboratory of Internet of Things Application Technology of the Ministry of Public Security of PRC，Beijing 100048，China）

Long and narrow space positioning problems are wide spread in the indoor positioning applications，the tradition almethod based on RSSI（Received Signal Strength Indicator）ranging is simple，but in long and narrow space，the RSS volatility and the shade of human body on wirelesss ignalcan seriously reduce the positioning accuracy.In this paper，the effect of human body shadow loss of long and narrow spaceis first analyzed，than combination positioning method is proposed，which skill fully combined RSSI ranging with extended Kalman filter positioning algorithm.That is，in the medium scale（5λ～50λ）using RSSI ranging method based on the human body penetration loss model，in large scale（＞50λ）using extended Kalman filtering algorithm based on the human body penetration amendment model.Experiments show that the positioning accuracy of the method in the longand narrow spaceis obviously better than the RSSI ranging positioning method.

long and narrow space；human body penetration loss；RSSI ranging；combination positioning method

TP393

A

1004-1699（2016）04-0601-05

2015-10-12修改日期:2015-12-31