核電廠反應堆冷卻劑系統旁路溫度高精度測量方法研究*

劉理云，曾喆昭

（1.婁底職業技術學院電子信息工程系，湖南婁底417000；2.長沙理工大學電氣與信息工程學院，長沙410076）

核電廠反應堆冷卻劑系統旁路溫度高精度測量方法研究*

劉理云1，曾喆昭2*

（1.婁底職業技術學院電子信息工程系，湖南婁底417000；2.長沙理工大學電氣與信息工程學院，長沙410076）

為了提高核電廠反應堆冷卻劑系統旁路溫度的測量精度，建立了鉑電阻溫度計的溫度-電阻特性曲線擬合模型和電阻-溫度特性曲線模型，采用遞推最小二乘法對樣本數據進行擬合以確定特性曲線的模型參數。該方法根據鉑電阻溫度計的測量電阻值即可高精度計算出相應的溫度。仿真結果表明，與現有方法相比，溫度測量精度有明顯提高，在溫度檢測領域具有重要的理論和應用價值。

電阻-溫度特性曲線；曲線擬合；遞推最小二乘法；鉑電阻溫度計

EEACC:7230doi:10.3969/j.issn.1004-1699.2016.04.025

鉑電阻溫度計具有靈敏度好、測溫準確度高、化學性質穩定可靠等優點獲得了廣泛應用［1-6］。核電廠反應堆冷卻劑系統的旁路溫度通常使用鉑電阻溫度計進行測量，而鉑電阻溫度計產生的電阻信號則由溫度采集卡根據標準進行電阻-溫度轉換，然后再通過校準模塊修正轉換后的溫度值與被測溫度的偏差［1］。由于校準模塊的修正模型通常使用二次曲線模型，而且只使用3個標定點下的電阻來確定修正模型，因而難以保證非標定溫度點的測量精度。針對只使用3個標定點下的電阻來確定修正模型的參數存在的局限性，文獻［1］使用了基于非線性最小二乘法的二次曲線擬合方法，建立了鉑電阻溫度計的電阻-溫度的關系函數，減小了整個測溫范圍內標定溫度值與實際溫度值的偏差，有效提高了旁路溫度測量通道的精度，然而，文獻［1］仍然難以保證鉑電阻溫度計的電阻-溫度特性的準確函數關系。文獻［7-8］使用最小二乘法進行分段多項式曲線擬合的方法對溫度非線性特性進行補償，研究結果表明，采用3次、4次分段多項式曲線擬合的非線性特性補償方法有效提高了溫度測量精度。然而，由于最小二乘法涉及微分運算，對測量噪聲和量化噪聲很敏感，難以進一步提高溫度測量精度。為此，文獻［9］提出了基于噪聲抵消技術的高精度溫度測量方法，該方法采用噪聲抵消算法克服了噪聲和隨機誤差對測量精度和穩定度的影響，有效提高了溫度測量精度和穩定度。此外，文獻［10］提出了一種改進型的分批估計自適應加權融合算法，并取得了一定效果。

為了進一步提高溫度測量精度，本文提出了一種基于遞推最小二乘法的代數多項式曲線擬合方法。該方法使用代數多項式曲線模型來擬合鉑電阻溫度計在所有標定點下的電阻-溫度特性關系，通過遞推最小二乘法確定代數多項式曲線模型的參數，有望獲得更高的溫度測量精度。

1　鉑電阻溫度計溫度-阻值特性的局限性

根據IEC60751《工業鉑電阻溫度計和鉑溫度傳感器》標準規定，當溫度在0～850℃的范圍時，溫度-阻值特性關系為［1，11］:

其中，t是溫度變量；R（t）是鉑電阻在溫度為t時的電阻值；R（0）是鉑電阻在溫度為0℃時的電阻值；A、B是關于鉑電阻溫度計溫度-阻值特性關系的兩個常數。

由式（1）可知，如果已知R（0）、A和B，則容易得到以R（t）為自變量的電阻-溫度特性關系函數t，即

由式（1）或式（2）可知，僅僅根據R（0）、A、B等三個參數難以準確反映鉑電阻溫度計的溫度-電阻特性函數關系或電阻-溫度特性函數關系。為此，下面介紹一種更能準確反映鉑電阻溫度計電阻-溫度特性函數關系的模型。

2　代數多項式曲線擬合模型

為了便于分析，取文獻［1］的鉑電阻溫度計測量數據如表1所示。

2.1鉑電阻溫度計的溫度-電阻特性擬合曲線模型

由于表1只給出了0～345℃范圍內標定溫度的測量電阻值，為了了解鉑電阻溫度計在0～850℃范圍的溫度-電阻特性關系函數，擬采用代數多項式模型進行特性曲線擬合。設基于n次代數多項式的擬合曲線模型表示為:

式中，x∈［-1，1］與溫度測量值t有關；cj是擬合曲線的模型參數，且 j=0，1，…，n；Rf（x）是被測電阻值的擬合函數。

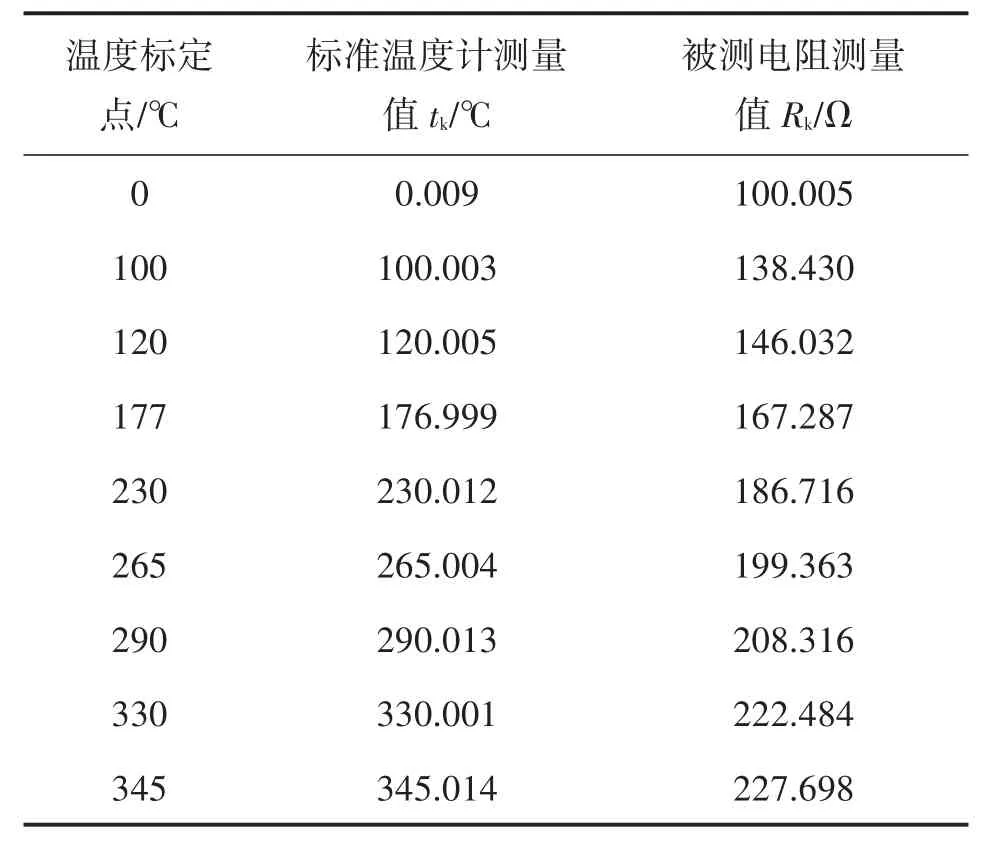
表1　鉑電阻溫度計測量值

由于鉑電阻溫度計的溫度標定范圍是0～850℃，因此，為了能夠有效使用式（3）所示的多項式模型來擬合表1中給出的測量數據，需要做如下變換:

或

對式（4）離散化，得

此時，式（3）變為:

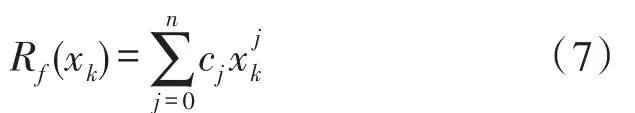
下面討論使用式（8）對表1所示的測量數據進行擬合，具體方法如下:

設電阻值擬合誤差為:

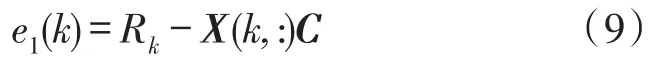
其中，Rk是表1所示的第k個被測電阻測量值。

性能指標為:

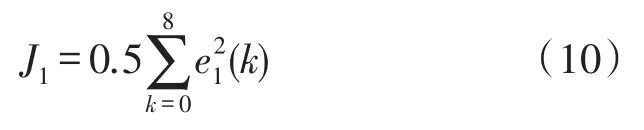
為了使性能指標J1最小，即minJ1，采用遞推最小二乘法來確定模型參數向量C，算法描述如下［12-13］:

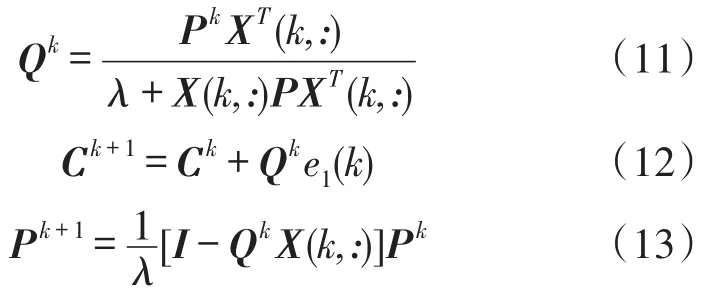
其中，初始協方差陣 P0=αI∈R（n+1）×（n+1），α=103～1010。λ是遺忘因子，通常取0.90≤λ≤1。當參數變化快時，λ取小點；變化慢時，取大點。當λ=1時，該估計公式成為基本遞推最小二乘算法。

根據式（9）～式（13）對表1所示的所有樣本數據進行迭代訓練后，可以獲得一組最優的多項式模型參數，使式（3）所示的代數多項式模型逼近表1所示的鉑電阻溫度計在標定溫度點下的被測電阻值。

2.2鉑電阻溫度計的溫度-電阻特性擬合仿真

仿真實驗1溫度-電阻特性擬合仿真

在仿真實驗中，取α=1010、λ=0.99、使用 3次代數多項式模型進行曲線擬合，仿真結果如圖1所示，其中黑點表示表1的測量值；實線表示3次代數多項式模型的擬合曲線。最優模型參數為 :C=［255.2367，143.9878，-11.9699，-0.7248］。由圖1（b）可知，被測電阻的最大絕對擬合偏差小于0.022 Ω，具有很高的擬合精度。

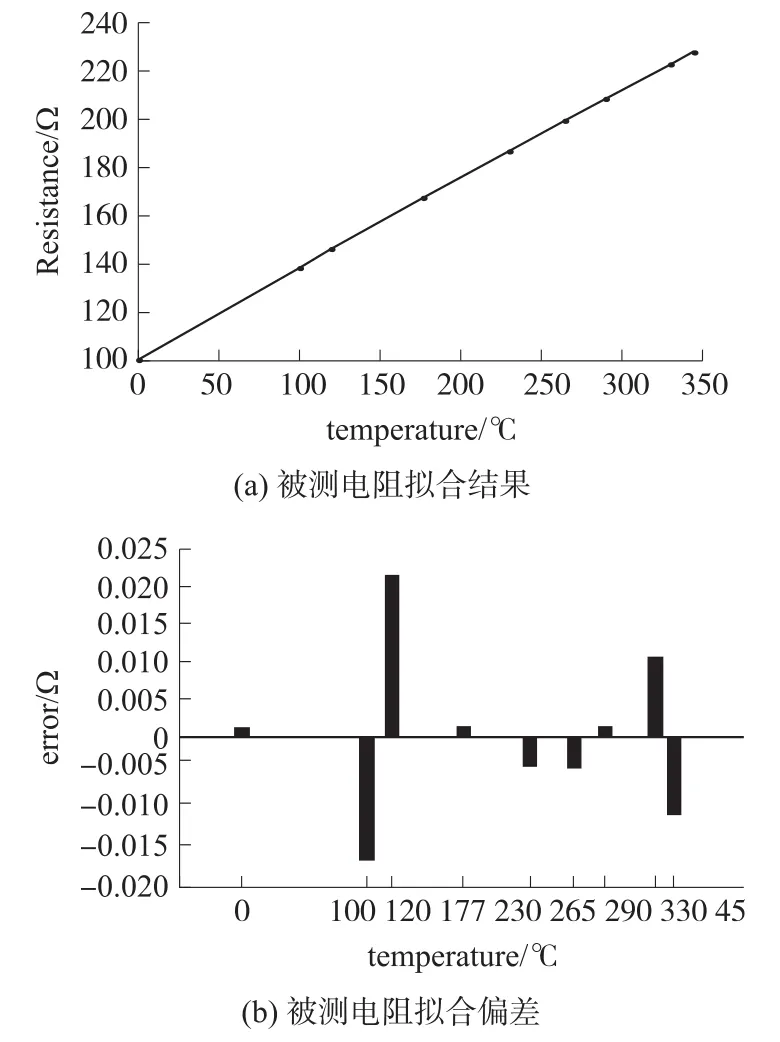
圖1　溫度-電阻特性曲線擬合結果

仿真實驗2溫度-電阻特性模型辨識仿真

盡管表1只給出了0～345℃范圍內標定溫度的測量電阻值，但是，通過仿真實驗1確定的最優擬合曲線模型，將標定溫度由0～345℃范圍拓展到0～850℃范圍時，通過式（8）可計算出標定溫度在0～850℃范圍時的相應鉑電阻溫度計的電阻值，如圖2所示。仿真結果表明，當標定溫度為850℃時，對應的鉑電阻溫度計的電阻值為:386.530 Ω。

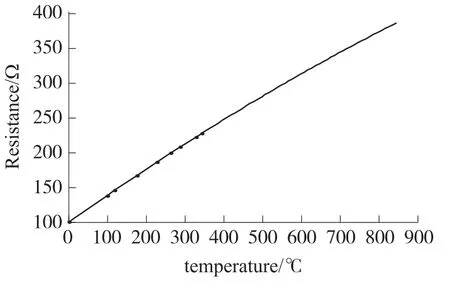
圖2　溫度-電阻特性模型辨識曲線

2.3鉑電阻溫度計的電阻-溫度特性擬合模型

2.1節和2.2節分別介紹了鉑電阻溫度計的溫度-電阻特性擬合曲線模型及仿真結果，表明了基于遞推最小二乘法的多項式模型在溫度-電阻特性曲線擬合中的有效性。然而，相應的反問題更具有實際意義:如何根據鉑電阻溫度計的被測電阻值來計算溫度計的溫度？仿照上述方法，下面具體介紹鉑電阻溫度計的電阻-溫度特性的曲線擬合原理。

設電阻-溫度特性曲線的擬合模型為:

其中，y∈［-1，1］與被測電阻值R有關；dj是擬合曲線的模型參數，且 j=0，1，…，n；T（y）是擬合的溫度函數。

由表1可知，標定溫度為0℃時，被測電阻為100.005 Ω；而根據仿真實驗2的計算結果可知:當標定溫度為850℃時，對應的鉑電阻溫度計的電阻值為:386.530 Ω。因此，作如下變換:

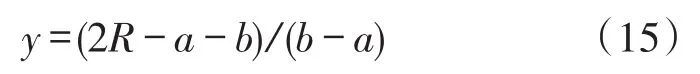
其中，a=100.005、b=386.530。對式（15）離散化:

則式（14）離散化為:

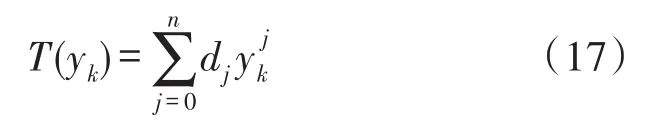
設向量:

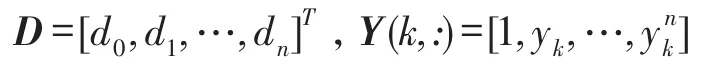
則式（17）可改寫為:

設溫度的擬合誤差為:

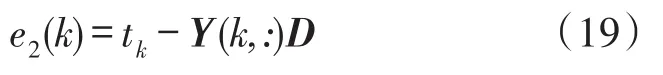
定義性能指標為:

為了使性能指標J2最小，即minJ2，采用遞推最小二乘法來確定電阻-溫度特性擬合模型參數向量 D=［d0，d1，…，dn］T，有關遞推最小二乘法如前所述。

仿真實驗3電阻-溫度特性擬合仿真

在仿真實驗中，取α=1010、λ=0.99、使用3次代數多項式模型進行電阻-溫度特性曲線擬合，仿真結果如圖3所示，其中黑點表示表1的測量值；實線表示電阻-溫度特性的擬合曲線。最優模型參數為:D=［389.8786，416.7482，31.3617，4.4897］。

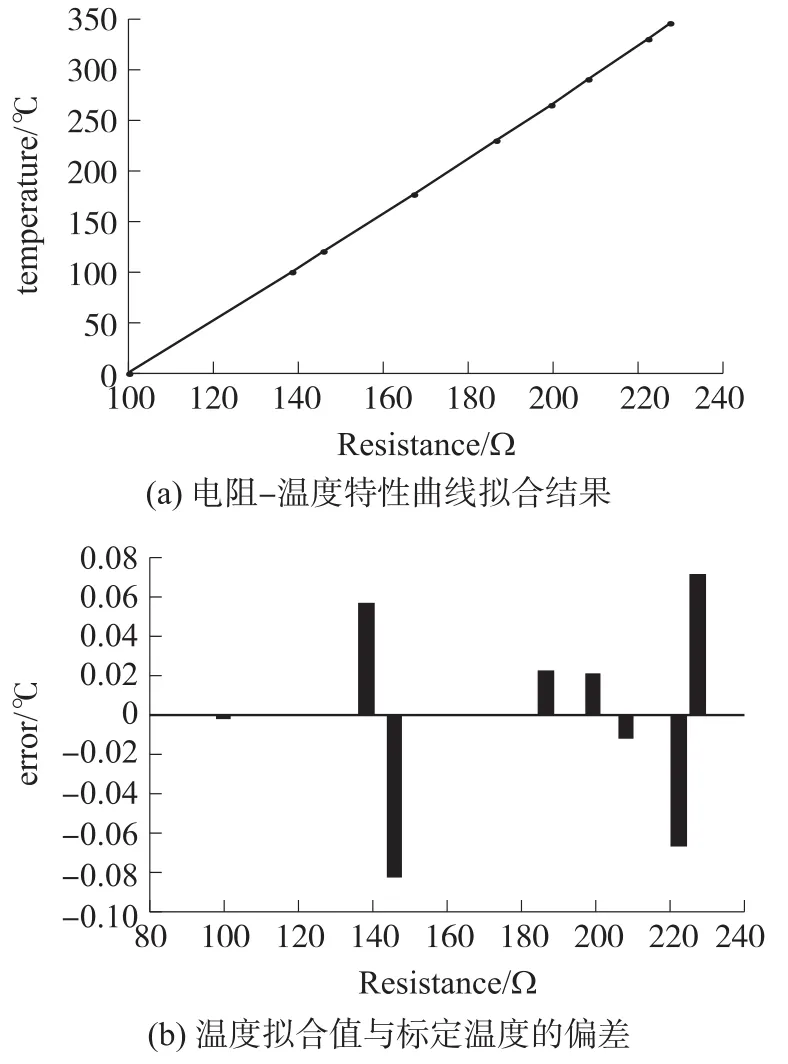
圖3　電阻-溫度特性曲線的擬合結果

由圖3可知，采用3次多項式模型擬合鉑電阻溫度計的電阻-溫度特性曲線時，最大絕對溫度偏差小于0.082℃。很顯然，與文獻［1］相比，鉑電阻溫度計的溫度測量精度有明顯提高。

仿真實驗4電阻-溫度特性測試實驗

為了驗證鉑電阻溫度計電阻-溫度特性曲線擬合模型的有效性，在被測電阻值為 100.005 Ω～386.530 Ω的全范圍時，采用上述3次代數多項式模型擬合的電阻-溫度特性曲線模型進行仿真計算，仿真結果如圖4所示。

由圖4可知，根據表1給定的9個樣本數據（電阻值在 100.005 Ω～227.698 Ω），即可建立100.005 Ω～386.530 Ω全電阻值范圍內的鉑電阻溫度計的電阻-溫度特性曲線模型。其中，在第9個電阻值樣本數據227.698 Ω后，電阻值的離散間隔為1 Ω。從圖4所示的電阻-溫度特性曲線最后一個小黑點（第9個樣本數據）以后的光滑曲線可以看出，優化構建的電阻-溫度特性曲線模型是有效的。仿真曲線最后一個樣本點是（385.698 Ω，839.617℃）。

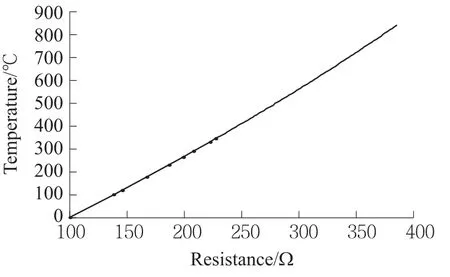
圖4　鉑電阻溫度計的電阻-溫度特性曲線

3　結論

論文分別提出了鉑電阻溫度計的溫度-電阻特性3次曲線擬合模型和電阻-溫度特性3次曲線擬合模型，并使用遞推最小二乘法對3次多項式曲線模型參數進行優化計算。仿真結果表明，根據有限樣本數據即可建立鉑電阻溫度計的完整特性曲線模型，其中，溫度-電阻特性的優化曲線模型為鉑電阻溫度計在標定溫度為850℃時對應的鉑電阻阻值的計算提供了理論模型，為后續的電阻-溫度特性曲線模型的建立奠定了理論基礎；而電阻-溫度特性的優化曲線模型完整刻畫了鉑電阻溫度計的電阻-溫度特性函數關系，根據被測的鉑電阻阻值即可高精度計算出鉑電阻溫度計的實際溫度，為核電廠反應堆冷卻劑系統旁路溫度的測量與控制奠定了理論基礎，進而為是否緊急停堆作出決策。

［1］ 陳靜，陳柯，霍雨佳，等.提高核電廠反應堆冷卻劑系統旁路溫度測量精度的方法［J］.核動力工程，2015，36（2）:93-95.

［2］ 秦洋陽，楊小秋，吳保珍，等.海底熱流探測中的高分辨率測溫技術［J］.中國科學:技術科學，2013，43（7）:816-821.

［3］ 韋彩虹，雷聲，朱國忠，等.婦科術后凝血用熱極探頭的溫度控制系統設計［J］.傳感技術學報，2011，24（8）:1087-1091.

［4］ 栗鵬飛，楊永平.提高太陽能熱泵系統溫度傳感器測量準確性的研究［J］.傳感技術學報，2014，27（8）:1017-1021.

［5］ 胡鵬程，時瑋澤，梅健挺.高精度鉑電阻測溫系統［J］.光學精密工程，2014，22（4）:988-995.

［6］ 朱杰，郭濤.一種Pt100溫度傳感器的動態熱響應模型［J］.傳感技術學報，2013，26（1）:73-77.

［7］ 吳志祥，周祥才，黃亮，等.多項式直接擬合在鉑電阻高精度測溫中的研究［J］.自動化與儀表，2014，35（2）:57-60.

［8］ 張鵬超，張強.一種NTC熱敏電阻校正方程的試驗研究［J］.傳感技術學報，2012，25（2）:220-223.

［9］ 方益喜，雷開卓，張群飛，等.基于噪聲抵消技術的高精度溫度測量系統［J］.計算機測量與控制，2013，21（8）:2074-2076.

［10］王華東，王大羽.一種改進的多無線傳感器數據分批估計自適應加權融合算法［J］.傳感技術學報，2015，28（8）:1239-1243.

［11］IEC 60751-2008.Industrial Platinum Resistance Thermometers and Platinum Temperature Sensors［S］.Geneva，International Electrotechnical Commission，2008.

［12］曾喆昭.神經計算原理及其應用技術［M］.北京:科學出版社，2012.

［13］曾喆昭，黃創霞，周富照.數值計算方法與應用［M］.北京:科學出版社，2013.

劉理云（1975-），男，副教授，主要從事應用電子技術、儀器儀表、自動控制研究，liuliyun1975@163.com；

曾喆昭（1963-），男，博士，教授，電路與系統學科負責人，電子科學與技術一級學科主要負責人，主要研究方向為智能檢測與智能控制，508984293@qq.com。

Method Research to Measure Bypass Temperature More Accurately of Reactor Coolant System in Nuclear Power Plants*

LIU Liyun1，ZENG Zhezhao2*
（1.Electron Information Engineer Department of Loudi Vocational&Technical College，Loudi Hunan 417000，China；2.College of Electric and Information Engineering，Changsha University of Science and Technology，Changsha 410076，China）

In order to improve the temperature measurement accuracy of bypass of the reactor coolant system in nuclear power plants，the models of temperature-resistance characteristic curve and resistance-temperature characteristic curve were established for a platinum resistance thermometer，and the parameters of the characteristic curve model were determined by using the recursive least square（RLS）algorithm for fitting sample data.The method can calculate the corresponding temperature more accurately according to the measured the resistance of platinum resistance thermometer.The simulation results showed that the temperature measurement precision was improved obviously compared with existing methods.Hence the method has important theoretical and application value in the field of temperature detection.

resistance-temperature characteristic curve；curve fitting；recursive least squares（RLS）；platinum resistance thermometer

TP271.5

A

1004-1699（2016）04-0622-05

項目來源:湖南省科技計劃項目（2014SK3227）

2015-11-02修改日期:2016-01-12