借助三角形中角的關(guān)系巧解題

◇　陜西　任艷寧

?

借助三角形中角的關(guān)系巧解題

◇陜西任艷寧

在解三角形問(wèn)題中除了常用的正弦定理、余弦定理及三角形面積公式以外,若能準(zhǔn)確把握各角之間的關(guān)系,往往能快速找到問(wèn)題的突破口．下面就這些關(guān)系的應(yīng)用舉例說(shuō)明．

1　利用三角形內(nèi)角和定理

(2) 求tanC的值.

2　利用三角形外角定理

圖1

(1) sin∠BAD;

(2)BD,AC的長(zhǎng).

所以

sin∠BAD=sin(∠ADC-B)=sin∠ADCcosB-

(2) 在△ABD中,由正弦定理得

在△ABC中,由余弦定理得

AC2=AB2+BC2-2AB·BC·cosB=

所以AC=7.

欲繼續(xù)求解,需要借助sin2∠BAD+cos2∠BAD=1,計(jì)算較為煩瑣,致使解題半途而廢．因此解題中要注意轉(zhuǎn)化的方向,盡可能地用已知來(lái)表示未知．

3　利用兩角互補(bǔ)關(guān)系

圖2

即

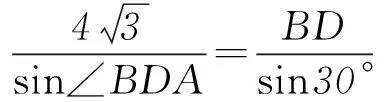
在△ADC中,由正弦定理得

即

又sin∠BDA=sin∠ADC,BD=CD,所以∠DAC=90°, ∠BAC=120°.

在△ABC中,由余弦定理

BC2=AB2+AC2-2AB·ACcos∠BAC,

得

4　利用2角互余關(guān)系

(1) 求B的值;

(2) 若點(diǎn)E、P分別在邊AB、BC上,且AE=4,AP⊥CE,求AP的長(zhǎng).

圖3

所以在Rt△ACP中,

陜西省渭南市大荔縣城郊中學(xué))