三角函數中最值問題解法探究
2016-09-28 06:45:07云南
高中數理化 2016年17期
◇ 云南 閔 敏 韋 歡
北京 童嘉森2(特級教師)
?
三角函數中最值問題解法探究
◇云南閔敏1韋歡1
北京童嘉森2(特級教師)
三角函數最值問題是三角函數中的基本內容,也是難點之一,對三角函數恒等變換、綜合應用能力要求較高.該內容重點考查學生轉化與化歸、函數與方程、數形結合等數學思想的應用,有一定的靈活性,要求學生具備一定的分析問題、解決問題、運算求解的能力,突破此內容要靠平時多積累.筆者歸納了求三角函數值域的3種方法與讀者分享.
1 用三角方法求三角函數的最值



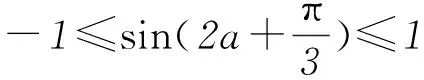


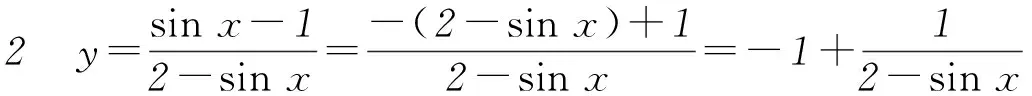

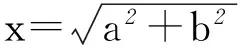
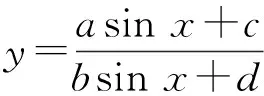
2 用代數方法求三角函數的最值


y=1-sin2x+2asinx=
-(sinx-a)2+a2+1.
若a>1,則當sinx=1時,
ymax=-(1-a)2+a2+1=2a.
若-1≤a≤1,則當sinx=a時,
ymax=-(a-a)2+a2+1=a2+1.
若a<-1,則當sinx=-1時,
ymax=-(-1-a)2+a2+1=-2a.
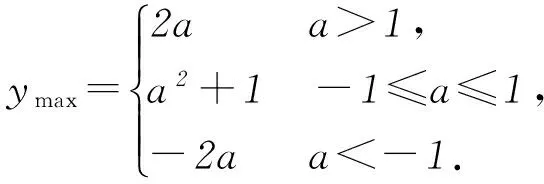


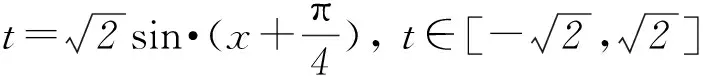
所以
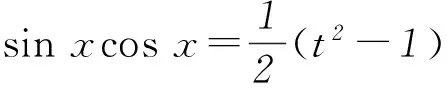
故
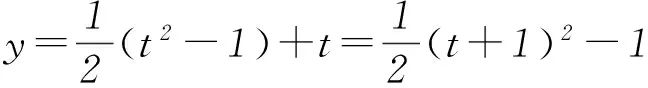
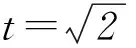
方法2y=sinx·cosx+sinx+cosx=
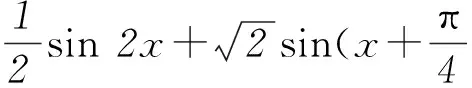
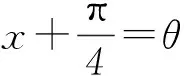
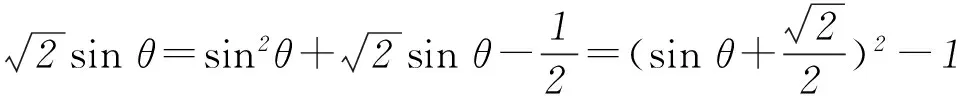
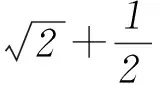


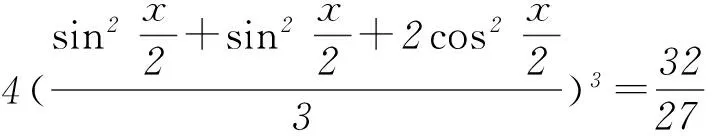
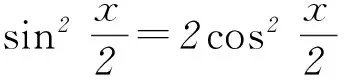
方法2y=cos3x+sin2x-cosx=cos3x+1-cos2x-cosx.
令cosx=t(-1≤t≤1),則
y=t3-t2-t+1(-1≤t≤1),
y′=3t2-2t-1=(t-1)(3t+1),
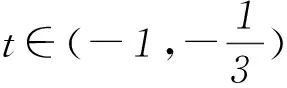
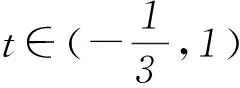
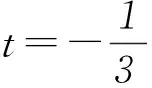

1) y=asin2x+bsinx+c
或
y=acos2x+bcosx+c(a≠0),
可通過令t=sinx或t=cosx轉化為關于t的二次函數在區間[-1,1]上的最值.
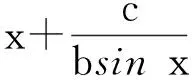
3)y=a(sinx±cosx)+bsinx·cosx.
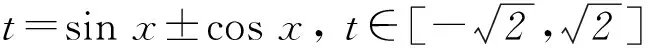

把三角問題轉化為代數問題解決.
以上3種形式可統稱為換元法,換元后一定要注意“新元”的取值范圍.
3 用解析法求三角函數的最值


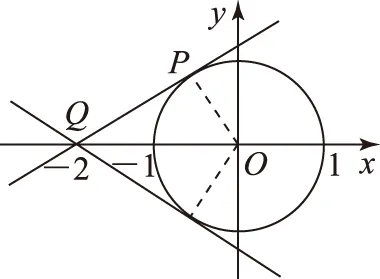
圖1
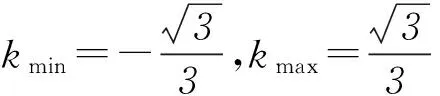
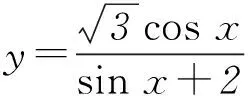
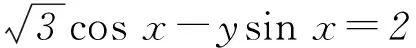
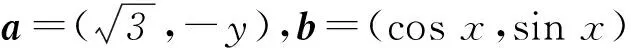


2sinx+(3-y)cosx=4-2y.
設 a=(2,3-y),b=(sinx,cosx).
由柯西不等式的向量形式|a·b|≤|a||b|得
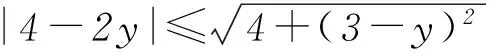
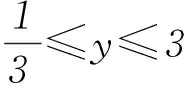


猜你喜歡
科學大眾(2022年11期)2022-06-21 09:20:52
中學生數理化·七年級數學人教版(2022年5期)2022-06-05 07:51:48
中等數學(2021年11期)2021-02-12 05:11:46
快樂語文(2018年13期)2018-06-11 01:18:16
中等數學(2018年11期)2018-02-16 07:47:42
臺聲(2016年2期)2016-09-16 01:06:53
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年4期)2015-05-19 14:47:56

