基于時(shí)滯思想的一類(lèi)非線(xiàn)性彈性桿結(jié)構(gòu)動(dòng)力行為的研究*

牛麗芳　張建文　段周波

(太原理工大學(xué)數(shù)學(xué)學(xué)院, 太原　030024)

?

基于時(shí)滯思想的一類(lèi)非線(xiàn)性彈性桿結(jié)構(gòu)動(dòng)力行為的研究*

牛麗芳?張建文段周波

(太原理工大學(xué)數(shù)學(xué)學(xué)院, 太原030024)

基于時(shí)滯思想,利用改進(jìn)的Galerkin方法,研究了一類(lèi)非線(xiàn)性彈性桿方程的長(zhǎng)時(shí)間行為.該方法將控制方程的解投影到由其線(xiàn)性算子的特征函數(shù)所張成的完備空間內(nèi),并截取有限階模態(tài)來(lái)逼近真實(shí)解,從而將無(wú)窮維動(dòng)力系統(tǒng)近似為有限維動(dòng)力系統(tǒng).根據(jù)時(shí)滯思想,構(gòu)造了反映高、低階模態(tài)關(guān)系的時(shí)滯表達(dá)式,使得在數(shù)值模擬過(guò)程中無(wú)需通過(guò)復(fù)雜數(shù)值積分即可直接獲取高階位移分量,從而降低了系統(tǒng)維數(shù),縮減了計(jì)算量.對(duì)系統(tǒng)進(jìn)行了數(shù)值模擬及分析,得到用較低的模態(tài)可描述系統(tǒng)解的最終狀態(tài).

時(shí)滯慣性流形,非線(xiàn)性Galerkin方法,非線(xiàn)性彈性桿

引言

設(shè)無(wú)窮維動(dòng)力系統(tǒng)

(1)

其中A在某一Hilbert空間V上是線(xiàn)性、自共軛無(wú)界算子,R是非線(xiàn)性算子.對(duì)給定的n∈N,Vn?V是n維子空間,記Pn是從V到Vn的L2_正交投影算子,并記Qn=I-Pn.記p=Pnu,q=Qnu,故u=p+q. 把Pn和Qn應(yīng)用到方程(1),則產(chǎn)生了一系列如下形式的方程

(2)

(3)

事實(shí)上,傳統(tǒng)的Galerkin方法相當(dāng)于在(2)中令q=0而得到的一系列有限維的動(dòng)力方程.

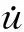
處于這樣的考慮,大家認(rèn)為對(duì)大多數(shù)微分動(dòng)力系統(tǒng)來(lái)說(shuō),一般依賴(lài)于系統(tǒng)的過(guò)去.為此,A Debussche和R Temam[4]提出了時(shí)滯慣性流形的概念,它說(shuō)明大小渦分量間的相互關(guān)系不是一種簡(jiǎn)單的瞬時(shí)作用,而是與渦的發(fā)展歷史相關(guān),即改變了慣性流形和近似慣性流形方法中高、低階分量……