一類分數階復雜網絡混沌系統的投影同步*
毛北行 李慶賓
(鄭州航空工業管理學院理學院, 鄭州 450015)
?
一類分數階復雜網絡混沌系統的投影同步*
毛北行?李慶賓
(鄭州航空工業管理學院理學院, 鄭州450015)
根據分數階系統的相關理論研究了一類分數階復雜網絡混沌系統的投影同步問題,給出了分數階復雜網絡以及分數階時滯復雜網絡系統實現投影同步的充分性條件,仿真結果表明了方法的正確性.
投影同步,分數階系統,復雜網絡
引言
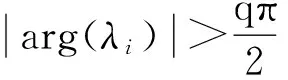
定義1[14]:Caputo分數階導數定義為:
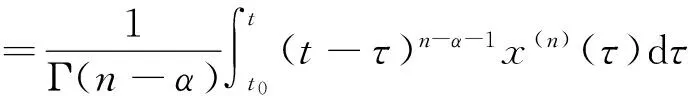
n-1<α 考慮如下一類分數階復雜網絡系統: ui(t)(i=1,2,…,N), (1) A為適當維數的常數矩陣,ui為控制輸入,Γ是網絡的內部耦合矩陣,C=(cij)N×N是外部耦合矩陣,滿足cij=0,(i≠j),cij≥0(i≠j),對角線元素定義為: (2) 假設1:復雜網絡的孤立節點的解滿足: Dtqs(t)=As(t)+f(s(t)) (3) s(t)可以是一個穩定點,或者周期解,也可以是混沌軌跡. 定義1: 對給定的分數階系統(1),若存在一個非零矩陣Λ,使得 假設2:非線性函數滿足條件: ‖f(xi(t))-Λf(s(t))‖≤li‖xi(t)-Λs(t)‖,其中li為大于零的常數. 定義系統誤差為: ei(t)=xi(t)-Λs(t), (i=1,2,…,N), 則有: Dtqei(t)=Aei(t)+f(xi(t))-Λf(s(t))+ 引理1[15]:對于一般的分數階自治非線性微分方程Dtαx(t)=f(x(t)),當系統的階數0<α≤1時,如果存在實對稱正定矩陣P,使得J(x(t))=xT(t)PDtαx(t)<0,則上述分數階系統漸近穩定. 定理1:設計控制器ui(t)=-kiei(t),若滿足條件(A+(li-ki)IN)+C?Γ<0則分數階復雜網絡系統(1)可以實現投影同步. 證明:由 Dtqei(t)=Aei(t)+f(xi(t))-Λf(s(t))+ C?Γ]ei(t)<0, 根據引理1,很容易得到定理1. 考慮如下一類分數階時滯復雜網絡系統: Dtqxi(t)=Axi(t)+f(xi(t-τ))+ (i=1,2,…,N), (5) A為適當維數的常數矩陣,ui為控制輸入,τ為時滯常數,Γ是網絡的內部耦合矩陣,C=(cij)N×N是外部耦合矩陣,滿足cij≥0(i≠j),同時對角線元素定義為: (6) 假設3:復雜網絡的孤立節點的解滿足: Dtqs(t)=As(t)+f(s(t-τ)) (7) s(t)可以是一個穩定點,或者周期解,也可以是混沌軌跡. 假設4:非線性……1 分數階復雜網絡系統的投影同步
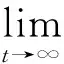
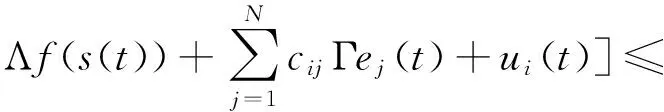
2 分數階時滯復雜網絡系統的投影同步

