廣義BBM方程的無(wú)窮序列新解*

李寧　套格圖桑

(內(nèi)蒙古師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院， 呼和浩特　010022)

?

廣義BBM方程的無(wú)窮序列新解*

李寧?套格圖桑

(內(nèi)蒙古師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院， 呼和浩特010022)

利用第二種橢圓方程的已知解與解的非線性疊加公式,構(gòu)造了廣義BBM方程的由Jacobi橢圓函數(shù)解、雙曲函數(shù)和三角函數(shù)組成的無(wú)窮序列新解.

第二種橢圓方程,解的非線性疊加公式,無(wú)窮序列新解

引言

眾所周知非線性波動(dòng)問(wèn)題是有許多物理背景的.非線性發(fā)展方程是研究此類物理問(wèn)題的重要數(shù)學(xué)模型,而非線性發(fā)展方程的求解等相關(guān)問(wèn)題是孤立子理論的重要研究?jī)?nèi)容之一.所以研究非線性發(fā)展方程的求解方法等問(wèn)題具有重要的研究意義.人們?yōu)榱藢ふ曳蔷€性發(fā)展方程的精確解,提出了許多有效的直接方法,也已取得了很多的成果[1-6].

文獻(xiàn)[7]構(gòu)造了廣義BBM方程(1)的由雙曲函數(shù)解、三角函數(shù)解、指數(shù)函數(shù)解和有理解構(gòu)成的有限多個(gè)新精確解.本文利用第二種橢圓方程的已知解與解的非線性疊加公式,構(gòu)造了廣義BBM方程(1)的由Jacobi橢圓函數(shù)解、雙曲函數(shù)和三角函數(shù)組成的無(wú)窮序列新解.

1　二種橢圓方程的相關(guān)結(jié)論

下面給出的第二種橢圓方程解的非線性疊加公式等結(jié)論,構(gòu)造廣義BBM方程(1)的無(wú)窮序列新解.

ut+αupux+βu2pux-δuxxt=0 (p>0,δ≠0)

(1)

1.1第二種橢圓方程的已知解

根據(jù)文獻(xiàn)[7]的相關(guān)結(jié)論,我們得到第二種橢圓方程

(2)

的如下解.

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

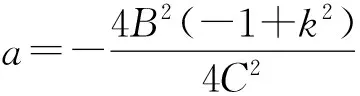
(15)

(16)

(17)

(18)

(19)

(20)

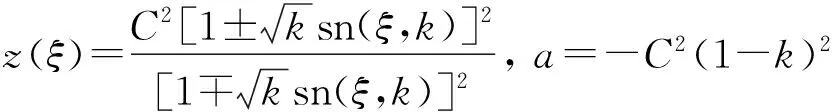
(21)

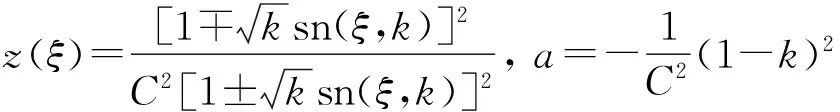
b=H,c=-C2(1-k)2

(22)

(23)

(24)

b=2(1+k2),c=B2(1-k2)2

(25)

z(ξ)=J7(ξ),a=B2(1-k2)2,

(26)

b=F,c=?16A2kP2

(27)

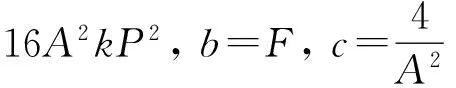
(28)

b=E,c=4Φ

(29)

(30)

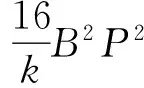
(31)

z(ξ)=L2(ξ),a=?16B2k2P2,

(32)

b=E,c=?16A2K

(33)

z(ξ)=L3(ξ),a=?16A2K,

(34)

(35)

(36)

b=E,c=?16C3K

(37)

z(ξ)=L5(ξ),a=?16C3K,

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

(48)

(49)

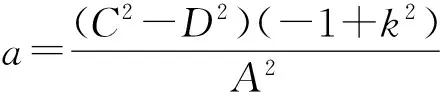
(50)

其中,J1(ξ)=C2[nd(ξ,k)±ksd(ξ,k)]2,

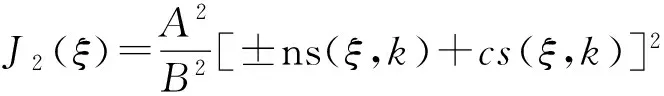
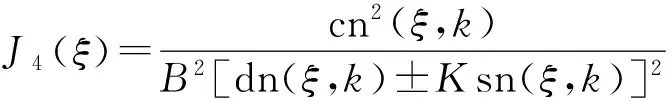
J5(ξ)=B2[dc(ξ,k)±Ksc(ξ,k)]2,

J6(ξ)=B2[dn(ξ,k)±cn(ξ,k)]2,

J7(ξ)=B2[ds(ξ,k)±cs(ξ,k)]2,

J8(ξ)=A2[ns(ξ,k)?ksn(ξ,k)]2,

J9(ξ)=B2[kcn2(ξ,k)±(1?k)]2,

F1(ξ)=A2[-(1?K)sn2(ξ,k)+1]2,

F2(ξ)=B2[k2cn2(ξ,k)+Θ]2,

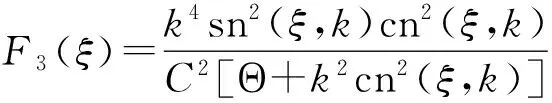
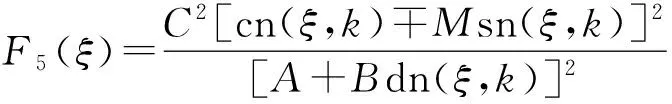
S1(ξ)=C2[dn(ξ,k)?Nsn(ξ,k)]2,

S2(ξ)=C2[dn(ξ,k)?Nsn(ξ,k)]2,

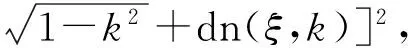
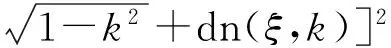
S5(ξ)=C2[?kcn(ξ,k)+dn(ξ,k)]2,

S6(ξ)=[Dcn(ξ,k)+Cdn(ξ,k)]2,

L2(ξ)=B2[dn2(ξ,k)-P]2ns2(ξ,k),

L3(ξ)=A2[-(1?K)sn2(ξ,k)+1]2nd2(ξ,k),

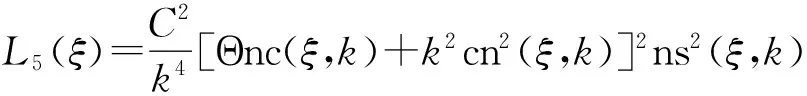
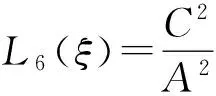
Φ=?4B2(±2(1-k2)+(k2-2)K),P=1?k,

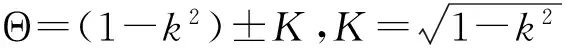
E=4(2-k2?6K),

F=4(-1±6k-k2),H=2(1+6k+k2),

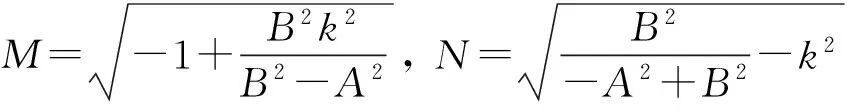
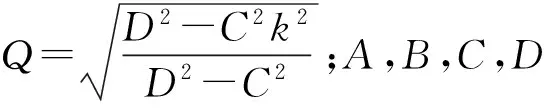
1.2第二種橢圓方程解的非線性疊加公式

若zn-1(ξ)是第二種橢圓方程(2)的非常數(shù)解,則下列zn(ξ)也是方程(2)的解.

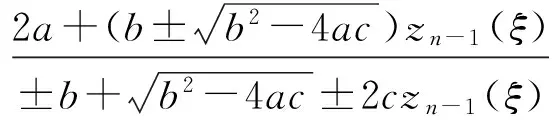
(51)

(52)

(53)

這里……