謀定而后動
——論解析幾何題的求解突破
葉 欣 江用科
(北京工業大學附屬中學,北京 100022)
?
謀定而后動
——論解析幾何題的求解突破
葉欣 江用科
(北京工業大學附屬中學,北京100022)
解析幾何的本質是用代數方法研究圖形的幾何性質,體現了數形結合的重要數學思想.我們在教學中,要教給學生分析問題的基本方法:首先要明確題目中的幾何問題是什么,然后分析幾何要素,思考如何進行轉化,最后再用坐標法進行推理、求解.
解析幾何數形結合轉化與化歸思想
解析幾何是高中數學的重要內容之一,在高考中占有重要地位.由于解析幾何解答題綜合性強,計算量大,因此是學生比較犯怵的一個考點,也是高考中拉開學生分數的題目,更是高三總復習中教師特別關注的一個專題.以北京高考為例,每年數學高考題的第19題基本都是有關解析幾何的題目,命題也主要以直線與圓錐曲線的位置關系為背景.在高三總復習的過程中,筆者發現學生并不理解解析幾何的本質,只是按照套路做題,有些學生甚至連圖都不畫,直接將直線方程與圓錐曲線方程聯立起來,消元得到一元二次方程,再利用根與系數的關系,列出等式,然后尋找有用的條件進行分析,如果遇到稍微復雜的題就只能碰碰運氣. 怎樣改變這種現狀呢?筆者就這個問題展開了深刻的思考,并在高三總復習的教學中進行了多種嘗試.通過引導學生對題目的分析,讓學生逐步理解解析幾何的本質,從而體會數形結合思想;引導學生合理設計解題思路,體會轉化和化歸思想,進而輕松解題.
一、分析幾何要素,進行數與形的轉化
【案例分析】學生見到此題時,通常會設出直線l的方程,將其與橢圓方程聯立,再利用P、Q兩點關于原點對稱這一特征,表示出P、Q兩點的坐標.進而表示出|PF2|、|QF2|的長度,最終求出△PF2Q的面積.依照這個思路,求解的過程非常復雜,只有少部分學生能得出最終結果.
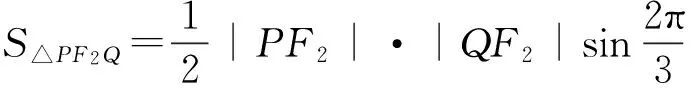
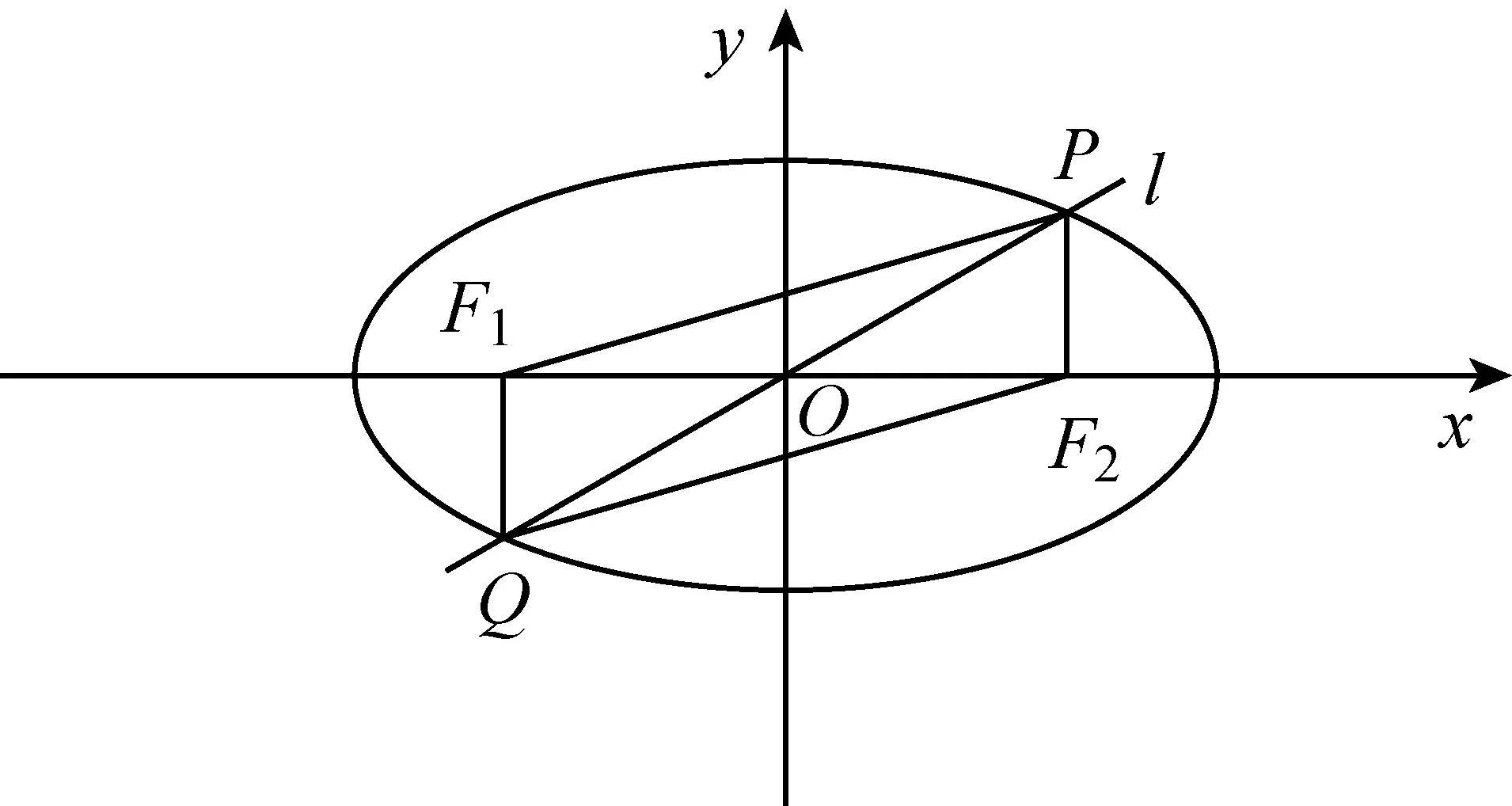
【解題過程】解:設橢圓的左焦點為F1,因為直線l過原點與橢圓交于點P,Q,由對稱性可知,四邊形PF1QF2是平行四邊形,所以△PF2Q的面積等于△PF1F2的面積.
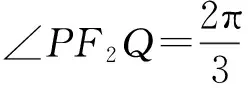
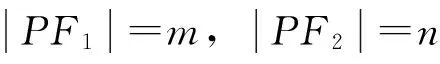

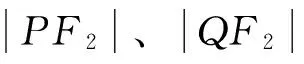
二、分析幾何要素,進行多角度的轉化
(Ⅰ)若直線l的方程為x+2y-1=0,求△OCD外接圓的方程;
(Ⅱ)判斷是否存在直線l,使得C,D是線段MN的兩個三等分點,若存在,求出直線l的方程;若不存在,說明理由.
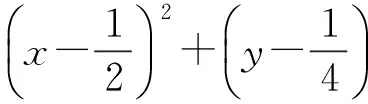
解法一:假設存在直線l,使得C,D是線段MN的兩個三等分點.
由題意,設直線l的方程為y=kx+m(km≠0),M(x1,y1),N(x2,y2),

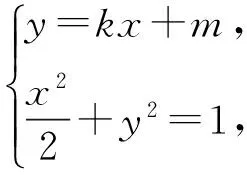
得(1+2k2)x2+4kmx+2m2-2=0,
所以Δ=16k2-8m2+8>0,
(*)
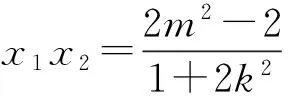
由C,D是線段MN的兩個三等分點,得線段MN的中點與線段CD的中點重合.
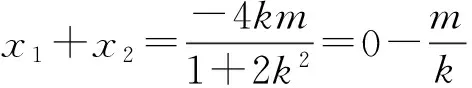
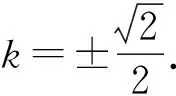
由C,D是線段MN的兩個三等分點,得|MN|=3|CD|.
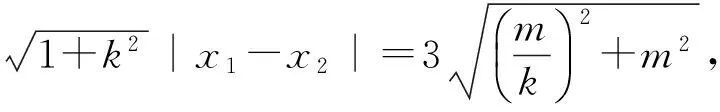
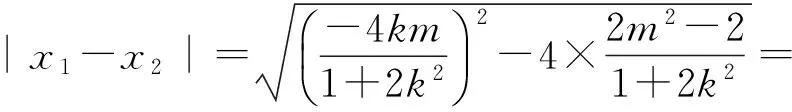
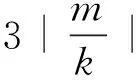
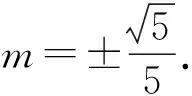
驗證知(*)成立.
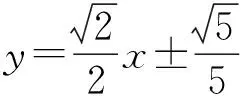
【教師引導與解題過程二】既然我們可以利用熟悉的中點解決問題,那是否可以將三等分點直接轉化為中點呢?實際上C,D是線段MN的兩個三等分點等價于|MD|=|DC|=|CN|,等價于C是DN的中點,且D是MC的中點,這樣利用中點坐標公式就可以直接求解.
解法二:假設存在直線l,使得C,D是線段MN的兩個三等分點.
由題意,設直線l的方程為y=kx+m(km≠0),M(x1,y1),N(x2,y2),

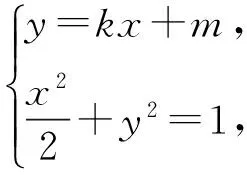
得(1+2k2)x2+4kmx+2m2-2=0,
所以Δ=16k2-8m2+8>0,
(*)
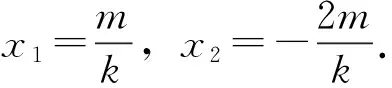
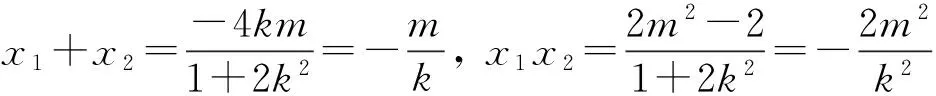
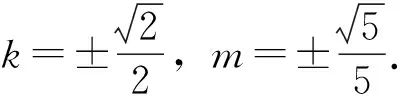
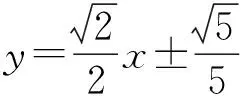
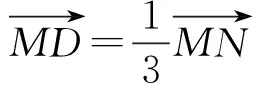
解法三:假設存在直線l,使得C,D是線段MN的兩個三等分點.
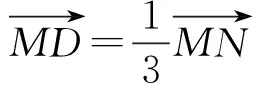
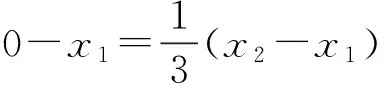
下同解法二.
【教師引導與解題過程四】上述三種解法都是先設出直線l的方程,進而表示出C,D的坐標,再將幾何條件轉化為代數問題,進行求解.求解本題是否還可以轉變一下思路呢?抓住C,D是坐標軸上的點,M,N是橢圓上的點這兩個條件,先設出C,D的坐標,再利用前面解法中轉化好的幾何條件表示出M,N的坐標,將其代入橢圓方程進行求解.
解法四:假設存在直線l,使得C,D是線段MN的兩個三等分點.
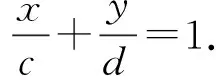
由C,D是線段MN的兩個三等分點,得C是DN的中點,且D是MC的中點,則M(-c,2d),N(2c,-d).
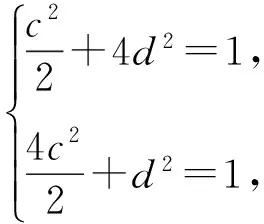
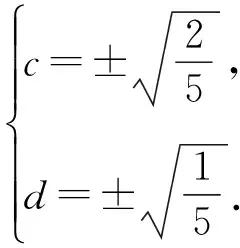
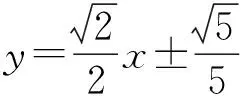
【案例總結】在高考中,解析幾何的解答題常與三角函數、向量、函數、不等式等內容綜合在一起考查,難度確實很大,如果我們能多花一些時間分析題目中的幾何問題,合理轉化題中涉及的幾何要素,先確定可行的解題方案,再動筆進行計算,就能輕松攻克解析幾何難關.
[1] 中華人民共和國教育部.普通高中數學課程標準(實驗) [S]. 北京:人民教育出版社,2003.
[2] 章建躍. 人教A版高中數學課標教材中的解析幾何[J]. 中學數學教學參考,2007(10).
[3] 王先進. 高三數學復習要抓實三個環節[J]. 中學數學月刊,2013(10).
[4] 張躍紅. 合理設計追求高效[J]. 數學通報,2013(10).
(責任編輯:李珺)

