基于拓撲優化的非均勻蜂窩結構設計與建模

文定良，金 鑫WEN Ding-liang， JIN Xin（.神華包頭煤化工有限責任公司，包頭 0400；.國防科學技術大學 機電工程與自動化學院，長沙 40073）

基于拓撲優化的非均勻蜂窩結構設計與建模

文定良1，金 鑫2
WEN Ding-liang1， JIN Xin2
（1.神華包頭煤化工有限責任公司，包頭 014010；2.國防科學技術大學 機電工程與自動化學院，長沙 410073）

蜂窩填充是實現結構輕量化的重要手段。針對均勻蜂窩結構未考慮最優傳力結構布局的缺點，提出了一種基于拓撲優化的非均勻蜂窩結構建模方法。對受力結構進行拓撲優化，將優化密度結果映射為蜂窩胞元的相對密度分布矩陣，通過用戶自定義特征以及參考基準的循環定義提高建模的自動化程度，實現非均勻蜂窩結構的快速建模。仿真結果表明，非均勻蜂窩結構力學性能更優，驗證了該方法的有效性。

蜂窩結構；拓撲優化；CAD建模；ANSYS仿真

0　引言

在航空航天、軌道交通等行業產品的設計中，結構的輕量化不僅可以減少產品制造與運行的能源消耗，而且可以為產品帶來更遠的射程、更高的機動性以及更優越的動靜態性能，是關系到產品競爭力的關鍵指標。近年來隨著材料制備和成形加工技術的迅速發展而出現的超輕蜂窩結構是以高孔隙率為特點，包含貫通或非貫通的二維或者三維孔隙的一類新穎多功能結構［1］。蜂窩結構具有低相對密度的特點，在結構減重的同時具有高比強度和比剛度，可以實現抗沖擊［2］、高效傳熱與隔熱［3］、電磁波吸收、吸聲降噪［4］，滿足多功能化的要求［5］。傳統蜂窩結構屬于周期性結構，相對密度分布均勻，制備工藝成熟，雖然從胞元尺度上來看其微結構是優化后的結構，但是從宏觀尺度上來說屬于未優化的均勻結構，這樣均勻分布的結構沒有考慮最優傳力路徑，輕量化效率不高。

拓撲優化是在滿足性能條件下實現輕量化目標的重要手段，其本質是在一定的外力和約束作用下，尋求具有最佳傳力路徑的結構布局形式［6］。拓撲優化在汽車、航空航天、土木工程以及工業裝備等領域的結構設計中發揮了越來越大的作用［7，8］，目前商業應用最成熟的是Rozvany［9］提出的SIMP（固體各向同性材料懲罰模型）方法，以設計空間每個單元的密度作為設計變量，最優設計結果是結構各部分的0～1之間的密度分布，可以將拓撲優化的最優密度結果向蜂窩胞元的相對密度進行映射，從而得到非均勻的蜂窩結構，在宏觀結構和細觀胞元兩個尺度實現結構的優化設計，提高結構輕量化效率。

蜂窩結構的建模有兩種方式，一是使用CAD平臺進行交互式建模，其問題在于：由于蜂窩胞元的非均勻特性，不便于使用陣列或鏡像等具有周期性的操作進行直接建模，手動建模復現難度大，成本高，時間周期長。二是使用快速成型前處理軟件，例如Magics。這一類軟件為基于STL格式模型的固定單元填充，該方案進行非均勻蜂窩結構建模的主要問題在于：非均勻結構實現困難，基本都只有均勻胞元填充功能，建模對象為STL格式，不利于優化設計后的結構處理調整，若結構生成后出現細節缺陷，需要返回CAD軟件中進行修改。因而，通過引入適當的方法對CAD軟件進行二次開發，提高建模自動化程度對于非均勻蜂窩結構的建模具有重要意義。

1　結構拓撲優化設計

對于非均勻蜂窩結構的拓撲優化，其參照結構是均勻密度的蜂窩結構，即通過拓撲優化實現在相同的減重比情況下的最大剛度。依據文獻［10］給出最小柔順性問題的一般性定義：在給定材料體積約束條件下，尋求設計域內材料的最優分布，實現最大化剛度的結構拓撲優化設計。因此對結構建立最小柔順度優化模型，以單元相對密度作為設計變量，在體積約束下求最大剛度，進行拓撲優化建模。

優化的目標函數為結構最大化剛度，也就是結構的柔度最小，柔度表達式為：

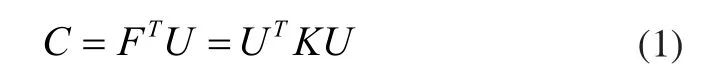
其中K是結構的整體剛度矩陣，可以表達為單元密度的函數，U是結構的位移矩陣，F是結構所受外力。約束條件包括體積約束、單元密度范圍約束以及其他約束。體積約束表示結構在固定的體積百分比范圍內進行單元密度排布，約束體積分數取初始均勻蜂窩結構的體積分數。單元密度范圍約束為考慮到密度過小單元胞壁過薄以及密度過大單元中心孔過小，都不利于制造，因此最小密度和最大密度取0.2和0.9。其他約束包括在設計時需要考慮的制造、使用方面的其他要求，以表示。由此可得，進行等效連續體結構拓撲優化的數學模型為：

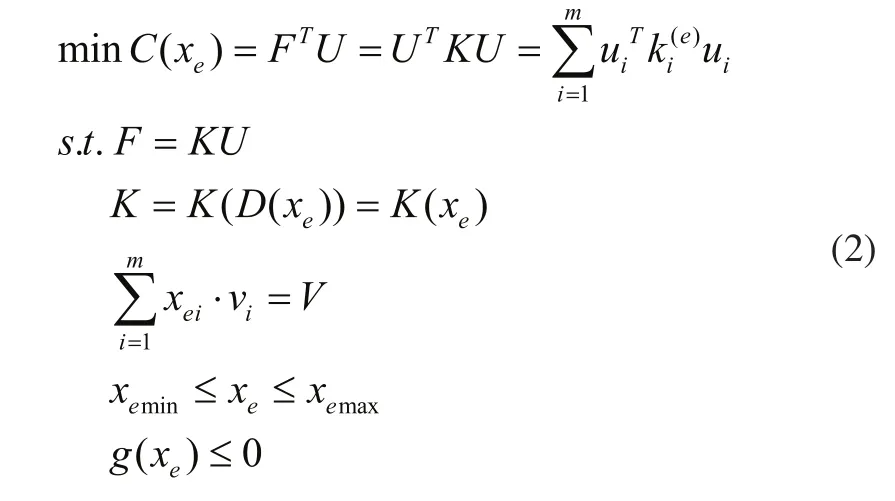
針對建立的優化模型，進行問題的求解的關鍵步驟是進行靈敏度分析，求得目標函數C對設計變量xe的靈敏度［10］：

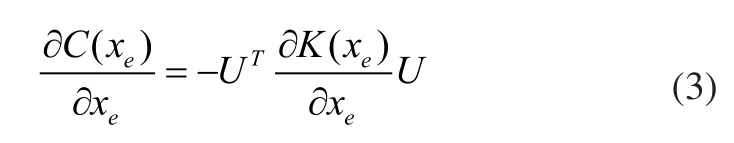
針對壁厚梯度約束等特定的設計要求，過濾并更新靈敏度函數，基于目標函數的靈敏度，采用優化準則算法優化更新設計變量［11］。

2　胞元密度矩陣映射

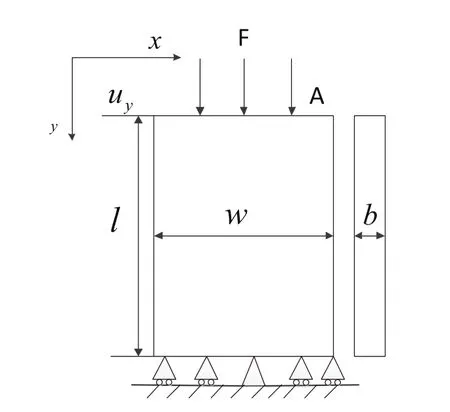
圖1　設計對象的幾何結構與受力狀況

針對具體設計對象如圖1所示，為長120lmm=，寬w=60mm，厚度b=10mm，頂端承受均布壓力F=60N的固體板狀設計域，胞壁實體材料彈性模量E=7.2×1010Pa，泊松比v=0.3。因為只承受蜂窩胞壁方向的力，參考Wang［12］進行的包括六邊形蜂窩、正方形蜂窩、全三角蜂窩在內的典型蜂窩結構力學性能對比分析，選擇正方形胞元構造變密度的蜂窩結構。以優化求解得到的單元密度矩陣為基礎，將胞元所在有限單元密度進行平均運算，映射求解胞元密度分布矩陣。具體過程如圖2所示，分為以下三步：

1）輸入參數確定。包括設計域長度length，設計域寬度width，胞元尺度a，拓撲優化有限單元尺寸r，拓撲優化單元密度矩陣xe。

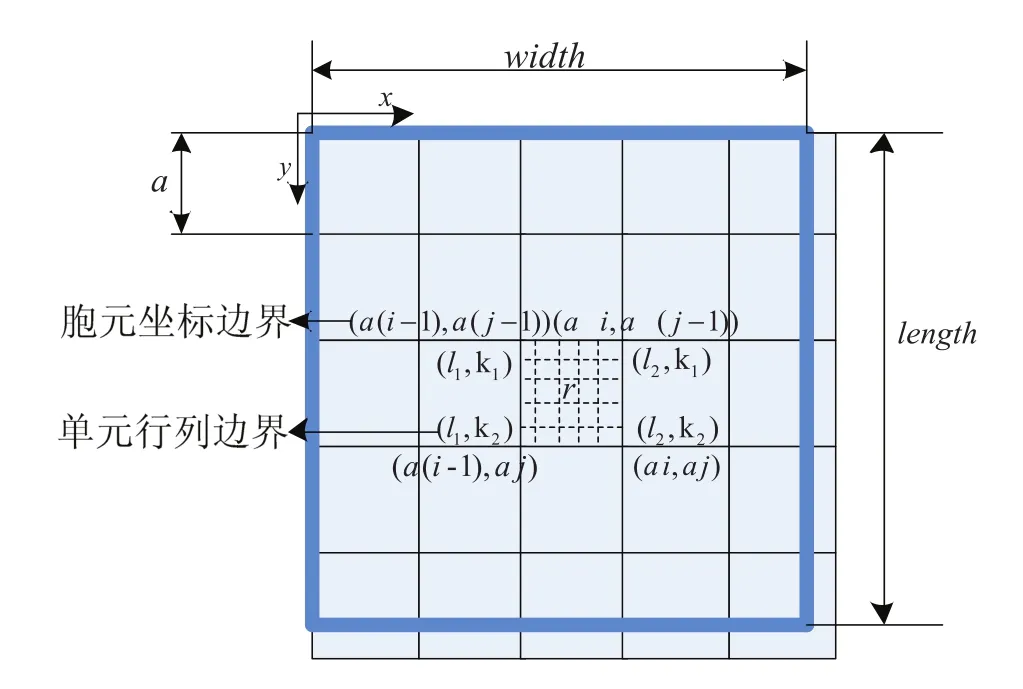
圖2　密度映射示意圖

2）胞元排布確定。以設計域左上角頂點作為胞元排布起始點，x方向胞元排布數目為y方向胞元排布數目為其中ceil表示可能出現邊緣胞元超出設計域情況，進行向上取整。

3）胞元密度矩陣求解。針對行為j、列為i的胞元。其胞元邊界坐標為：

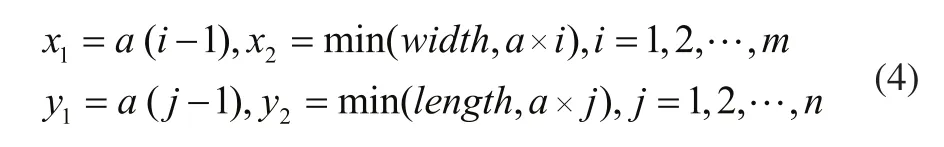
胞元所在有限單元密度矩陣的對應邊界行列為：

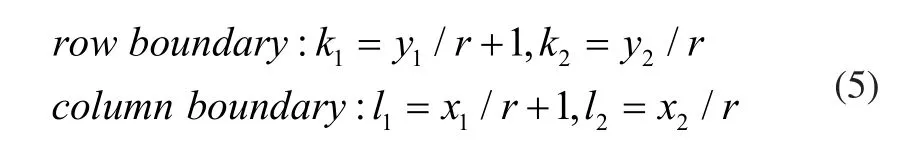
對行列范圍內的有限單元密度進行平均化求解，得到胞元的映射密度：

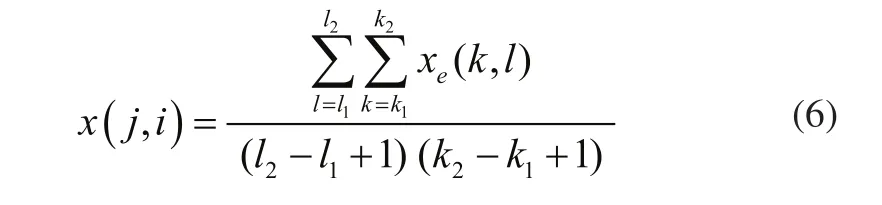
3　非均勻蜂窩結構建模

以映射得到的胞元排布和密度矩陣為輸入，進行變密度蜂窩結構的建模，本文選擇PTC公司的Creo作為結構建模CAD軟件，使用Creo中的用戶自定義特征（UDF）方法簡化建模過程，基于其功能豐富的Pro/ Toolkit函數庫進行Creo的二次開發，編寫變密度蜂窩結構自動建模生成的輔助應用程序。

非均勻蜂窩結構建模的總體流程如圖3所示，首先分析需要導入的蜂窩胞元特征，建立參數化模型與參考基準列表，依此完成胞元UDF的創建。正方形胞元結構UDF示意圖如圖4所示。圖中關鍵參數與參考基準如表1所示。構成參數化的UDF。

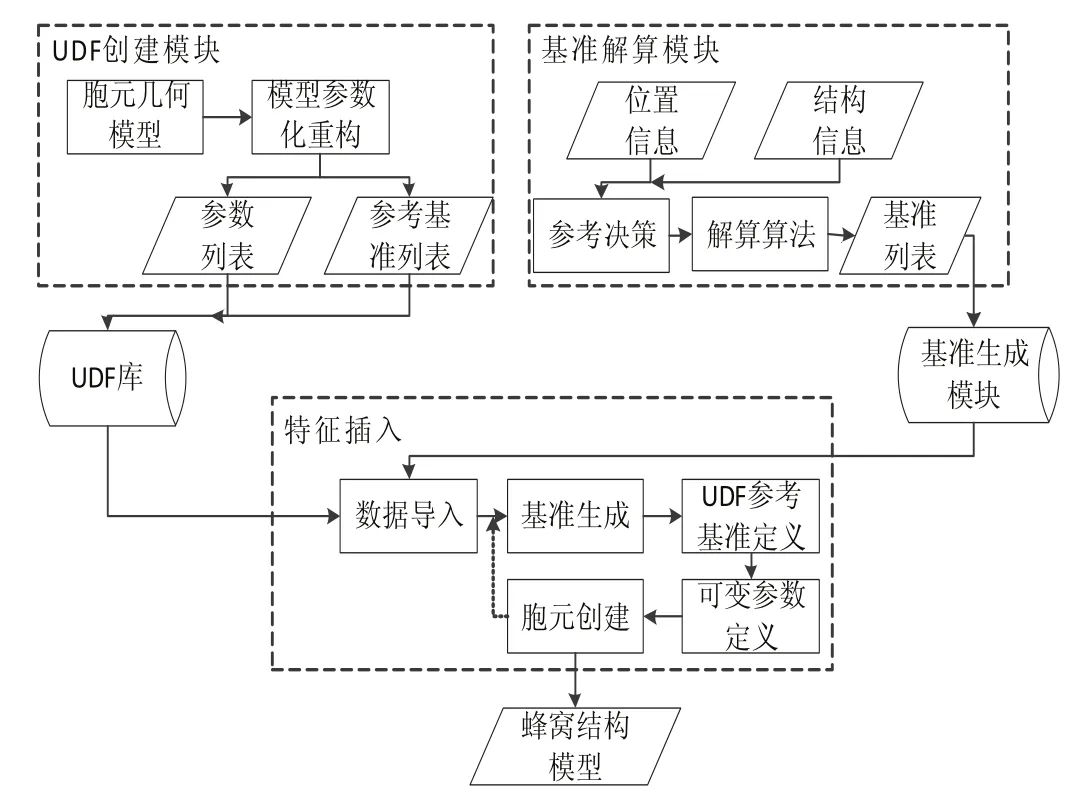
圖3　非均勻蜂窩結構建模流程圖

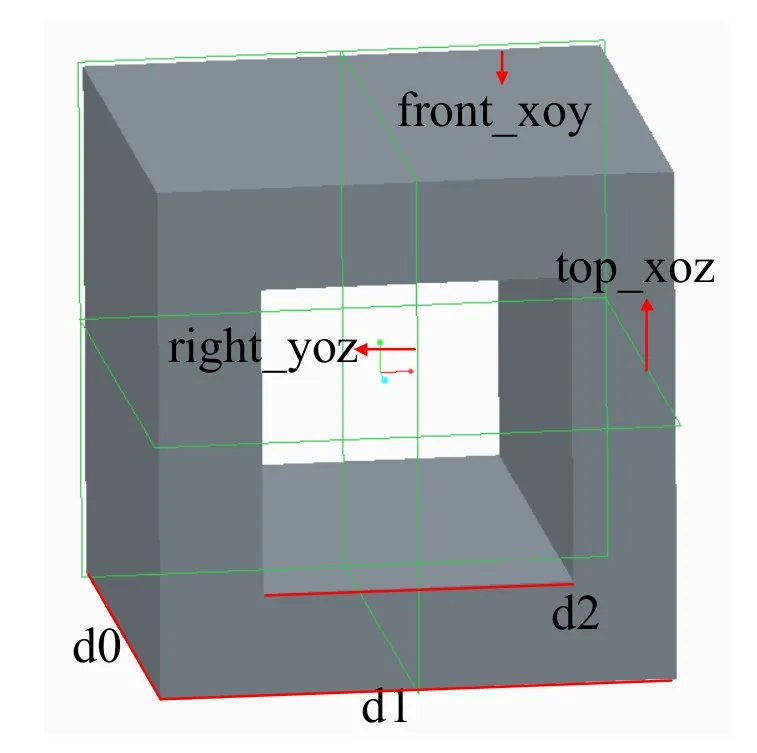
圖4　正方形胞元結構UDF

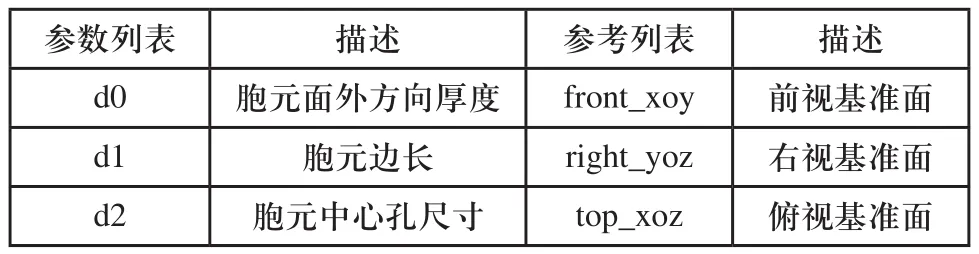
表1　正方形胞元參數與參考列表

胞元尺寸參數與胞元相對密度x之間滿足以下關系式，從而確定各胞元的基本參數取值。

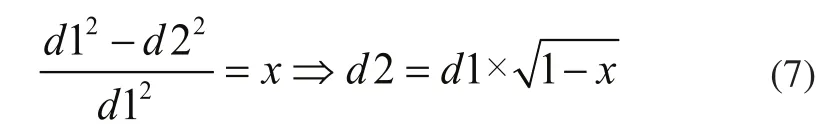
第二步將依據位置信息與胞元結構信息生成基準的功能封裝為基準生成模塊，基準面的類型包括默認基準面與偏距基準面。默認基準面是系統在默認初始坐標系下的三個標準正交平面，是起始胞元的參照；其他胞元的基準為偏距基準面，以默認基準面為參考，需要定義偏距值以及基準排布個數，其中偏距值為胞元邊長d1，基準排布為第2節中確定的x方向胞元排布數目和y方向胞元排布數目。

最后將胞元UDF與基準生成模塊結合，導入設計域尺寸、胞元外形尺寸以及胞元密度矩陣數據，基于這些數據進行參考基準的生成及可變參數的賦值，實現對各個單胞的空間位置及形狀的循環定義，生成變密度蜂窩結構模型。

4　結果及其分析

圖1所示對象的拓撲優化密度分布以及非均勻蜂窩結構建模結果如圖5所示。經過密度映射以及CAD建模后的蜂窩結構模型完整無缺陷，能夠較好地反映拓撲優化的密度分布。

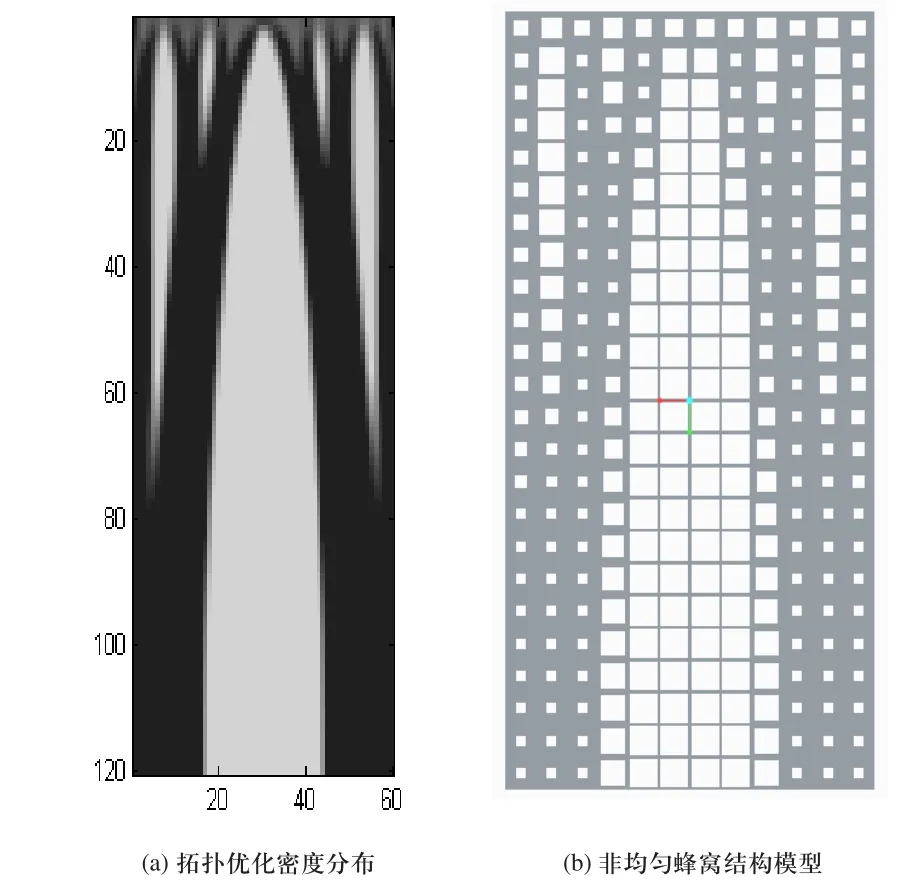
圖5　優化設計與蜂窩結構建模結果對比

采用ANSYS作為仿真分析工具，對均勻蜂窩結構以及非均勻蜂窩結構的抗壓剛度進行分析對比，其中uy為受壓頂部所有單元的y方向平均位移，F為頂部受到的壓力。蜂窩結構受壓變形如圖6所示。

圖6　蜂窩結構受壓變形對比

計算得到均勻蜂窩結構的抗壓剛度為145197N/ mm，非均勻蜂窩結構的抗壓剛度為164383N/mm，剛度提升幅度為13.2%，在相同減重比情況下，拓撲優化后的變密度蜂窩結構抗壓剛度相比均勻密度蜂窩結構剛度有明顯提高，驗證了基于拓撲優化的非均勻蜂窩結構建模的有效性。

5　結論

1）提出了一種基于拓撲優化的非均勻蜂窩結構建模方法。對受力結構進行拓撲優化，將優化密度結果映射為蜂窩胞元的相對密度分布矩陣，通過用戶自定義特征以及參考基準的循環定義提高建模自動化程度，實現非均勻蜂窩結構的快速建模。

2）經過密度映射以及CAD建模后的蜂窩結構模型完整無缺陷，能夠較好地反映拓撲優化的密度分布。

3）分析對比了均勻蜂窩結構以及非均勻蜂窩結構的抗壓剛度，結果表明優化后的非均勻蜂窩結構抗壓剛度性能更優，驗證了基于拓撲優化的非均勻蜂窩結構建模方法的有效性。

［1］ Wadley H N G.Multifunctional periodic cellular metals［J］.Phil Trans R Soc A，2006，364：31-68.

［2］ Elnasri I，Pattofatto S，et al.Shock enhancement of cellular structures under impact loading： Part I Experiments［J］.J Mech Phys Solids，2007，55（12）：2652-2671.

［3］ Tian J， Kim T，Lu T J， et al. The effects of topology upon fluidflow and heat-transfer within cellular copper structures［J］.Int J Heat Mass Transf，2004，47：3171-3186.

［4］ Wang J， Lu T J，Woodhouse J， et al. Sound transmission through lightweight double-leaf partitions： theoretical modeling［J］.J Sound Vibr，2005，286：817-847.

［5］ Fan H L， Jin F N， Fang D N.Mechanical properties of hierarchical cellular materials： Part I Analysis［J］.Compos Sci Technol， 2008，68：3380-3387.

［6］ 左孔天.連續體結構拓撲優化理論與應用研究［D］.長沙：國防科學技術大學，2010.

［7］ Zuo Kongtian. Research of theory and application about topology optimization of continuum structure［D］.Changsha：National University of Defense Technology，2010.（in Chinese）

［8］ Gil Ho Yoon.Maximizing the fundamental eigenfrequency of geometrically nonlinear structures by topology optimization based on element connectivity parameterization［J］.Computers and Structures，2010，88：120-133.

［9］ Soren Halkj?r， Ole Sigmund，Jakob S Jensen.Maximizing band gaps in plate structures［J］.Struct Multidisc Optim，2006，32：263-275.

［10］ Rozvany GIN， Zhou M，Birker T. Generalized shape optimization without homogenization［J］.Struct Optim，1992，4：250-254.

［11］ Bendsoe M P. Topology Optimization：Theory，Methods and Applications［M］.Berlin： Springer，2003.

［12］ Erik Andreassen，Anders Clausen，et al.Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip.Optim，2011，43（1）：1-16.

［13］ Wang A J， McDowell D L. In-plane stiffness and yield strength of periodic metal honeycombs［J］.ASME J Eng Mater Technol，2004，126：137-156.

Design and modeling of non-uniform honeycomb structures based on topology optimization

TN95

A

1009-0134（2016）08-0130-04

2016-07-29

文定良（1964 -），男，湖南人，高級工程師，工程碩士，主要工作內容為石油化工及煤化工的設備技術管理及工程管理。