基于NESSUS的兆瓦級永磁直驅風力發電機輪轂可靠性分析

周新建，李志強，涂宏斌ZHOU Xin-jian， LI Zhi-qiang， TU Hong-bin（.華東交通大學 機電工程學院，南昌 33003；.華東交通大學 軌道交通學院，南昌 33003）

基于NESSUS的兆瓦級永磁直驅風力發電機輪轂可靠性分析

周新建1，李志強1，涂宏斌2
ZHOU Xin-jian1， LI Zhi-qiang1， TU Hong-bin2
（1.華東交通大學 機電工程學院，南昌 330013；2.華東交通大學 軌道交通學院，南昌 330013）

輪轂的結構可靠性對于保障整套風力發電機系統的可靠性具有重要的作用。以1.5MW永磁直驅風力發電機的輪轂作為研究對象，利用有限元軟件對其進行初步的靜力分析，驗證其強度安全。考慮輪轂材料力學屬性的隨機性以及工作載荷的隨機性，將材料屬性參數（彈性模量Ex、泊松比Prxy、屈服強度σS）以及各葉片葉根工作載荷參數作為隨機變量引入到極限狀態方程中。利用專門的可靠性分析軟件NESSUS聯合ANSYS的靜力分析模型對輪轂結構強度進行可靠性分析，最終得到輪轂的結構可靠性指標以及各影響參數的靈敏度指標。

1.5MW永磁直驅風力發電機輪轂；靜力分析；可靠性分析；靈敏度指標；NESSUS

0　引言

兆瓦級風力發電機因其體型龐大、結構復雜、工作環境嚴酷（如曠野、海邊等），由此帶來的問題就是故障率的升高。根據行業要求，對于大型聯網運行的風機，可維修壽命需在20年以上，年利用率要在97%以上［1］，要實現如此高的可靠性指標，就須對風機進行可靠性和維修性設計，風機關鍵部件的可靠性設計就是其中重要的一部分。

輪轂作為風機的關鍵部件之一，它不僅需要承擔來自葉片的交變載荷，還需作為變槳系統的支撐以及將轉矩傳遞給直驅同步發電機的動軸。因此，在設計階段將輪轂的結構可靠性納入考慮之中對于保障整套風機的可靠性具有重要作用。現有對風力發電機輪轂的研究大多局限于對輪轂的結構強度或者疲勞強度進行分析計算［2～4］，少數涉及到對輪轂進行可靠性分析的，也僅僅是根據應力-強度干涉模型將輪轂的強度和應力簡單地設置成隨機正態分布，但兩者分布參數（均值μ和標準差σ）都是粗糙地根據經驗選取［5］，并沒有深入地分析輪轂應力和強度分布的影響因素。

本文對某1.5MW永磁直驅風力發電機的輪轂進行可靠性分析，根據強度-應力干涉理論，建立了輪轂的極限狀態模型，將輪轂的載荷參數以及材料的彈性模量Ex，泊松比Prxy以及屈服強度σS都作為隨機變量引入到極限狀態模型中，利用ANSYS聯合專門的可靠性分析軟件NESSUS，對風機輪轂進行了可靠性分析，定量地給出了輪轂的可靠性指標及各影響因素的靈敏度指標。其中，NESSUS作為專門的可靠性分析軟件，已經被廣泛地應用到諸多領域［6，7］。

1　風機輪轂功能簡介及模型建立

永磁直驅風力發電機內部主要的關鍵性零部件有：葉片、輪轂、永磁同步發電機（定子主軸+轉動軸+定子+轉子+轉子制動等）、機艙底座等，具體如圖1所示。

圖1　直驅風力發電機內部結構示意圖

其中，輪轂3聯接風力發電機的三個葉片，三個葉片對稱安裝在輪轂上，輪轂承擔來自葉片的交變載荷，同時將轉矩傳遞給永磁同步發電機的的轉軸，除此之外，輪轂上還安裝有三套獨立的葉片變槳系統，輪轂模型如圖2所示。

圖2　1.5MW永磁直驅風力發電機輪轂模型

2　基于ANSYS的輪轂有限元分析

將輪轂模型導入ANSYS軟件中，考慮到輪轂所受載荷主要來自于葉片，而葉片對輪轂的受力變形具有很大的影響，因此在對輪轂進行分析時，在輪轂的三個葉片接口處分別放置一段葉片的假體。由于后續可靠性分析需要調用輪轂有限元分析的過程和結果文件，因此葉片假體的添加以及后續的網格劃分、邊界條件施加等都通過ANSYS的參數化語言APDL完成。

2.1輪轂有限元分析模型的建立

風力發電機輪轂和三組葉片都采用10節點四面體單元SOLID187單元劃分網格，其中輪轂單元共計69910個，節點共計115278個，總體單元共計112455個，節點共計192874個，輪轂有限元模型如圖3（a）所示。

2.2輪轂及葉片假體材料力學屬性的賦予

輪轂及葉片的材料直接決定其屈服強度等力學屬性，輪轂及葉片所選用材料的材料參數如表1所示。

表1　輪轂及葉片的材料屬性參數

2.3載荷以及邊界條件的施加

風力發電機葉片以及變槳系統的重力，旋轉的離心力和慣性力、風吹過葉片產生的氣動載荷以及輪轂本身的重力構成了輪轂載荷。其中，葉片對輪轂的載荷都是集中在葉片和輪轂的聯接位置，也就是葉根中心位置，因此在施加葉片對輪轂的載荷時，在葉片-輪轂的聯接面中心建立節點，葉片對輪轂的載荷施加在其中心節點上，中心節點通過剛性梁單元MPC184與葉片假體上截面節點聯接，模擬葉片傳力，輪轂與主軸屬于剛性聯接，因此直接限制輪轂與轉動主軸法蘭聯接面的所有自由度，同時為了約束葉片的軸向旋轉，因此約束三個葉根聯接面中心（即載荷加載點）的Z向的旋轉，具體如圖3（b）所示。

對輪轂的強度分析涉及到風機的全部工況，根據GH Bladed軟件的仿真結果，可以得到葉片對輪轂的作用載荷，選取12種極限工況的載荷條件作為輪轂應力分析的基礎，而載荷大小和方向都是根據葉根坐標系給出的。

2.4輪轂靜力分析結果

根據輪轂的有限元分析結果，得到輪轂在各工況載荷條件下的最大等效應力情況如表2所示。

表2　各工況載荷輪轂最大等效應力數值

由此可以得到輪轂應力最大的為工況6，即1.318-yz 的83.91MPa，其中最大極限工況的具體載荷參數如表3所示，表中彎矩為kNm，力為kN，工況6載荷下輪轂的應力云圖以及變形云圖如圖3（c）、圖3（d）所示。

表3　最大極限工況載荷參數

圖3　輪轂有限元模型及應力分析結果

分析得到輪轂最大極限應力σmax= 83.91MPa，輪轂材料的屈服強度為σs= 200MPa，安全系數n=1.5，因此n×σmax<σs，輪轂強度符合靜力學強度要求。

3　結構可靠性分析理論及分析方法

3.1 結構可靠性計算

系統可靠性都是由其部件的可靠性組成，在計算單一部件的結構可靠度時，一般是基于應力-強度干涉模型，通過分析其主要失效模式，從而建立如式（1）所示的極限狀態方程。

其中，S為應力，代表能夠導致部件失效的因素；R為強度，代表相應的該部件所能承受極限值；g<0為失效區域，g>0是安全區域。考慮到工作載荷、尺寸參數以及材料參數的隨機性影響，方程中的應力S，強度R也都是在一定范圍內變化的隨機變量，兩者的干涉如圖4所示。

圖4　應力-強度干涉模型

由應力-強度干涉模型可知，應力S在［x， x+dx］范圍內的概率為A1陰影部分面積fs（x）dx。若強度R>x，則為可靠區域，其概率為A2陰影部分面積，具體如式（2）所示。如果將x變為在應力S范圍內的隨機變量，則強度R

始終大于應力S的概率如式（3）所示。

3.2基于設計驗算點（MPP）的可靠性指標的定義

在實際的結構可靠性計算的過程中，零部件的極限狀態方程可能由n個基本變量共同決定，如式（4）所示。

其中x1～xn一般是呈正態分布的隨機變量，利用當量正態法將X轉化為標準的正態分布U，則極限狀態函數g（X）變換成g（U），在標準正態分布的U空間中，f（u1，u2，…，un）=0為失效面，從坐標原點到失效面f（U）=0的最短距離β，即為所求可靠性指標，部件的失效概率Pf=Φ（-β）。

圖5為二維的標準化坐標系中可靠性指標定義的情況示意圖，由二維推及到n維，其中P為設計驗算點（MPP），其坐標為即為坐標原點到失效面的最短距離β，為設計驗算點P處的單位法線向量，三者之間的關系如式（5）所示。在實際工程計算中，αi和β可以通過迭代的方式求解出來。

靈敏度因子為失效狀態函數在設計點處的變化梯度，在確定性分析中，靈敏度的定義為在概率分析中，靈敏度定義為，表示概率隨分布參數（如均值和方差）的改變而變化的程度，同時概率靈敏度分析還可以用于確定每個隨機變量的重要性，而設計驗算點P處的單位法線向量在U方向上來的投影，即其矢量的余弦值即可代表靈敏度，如式（6）所示。

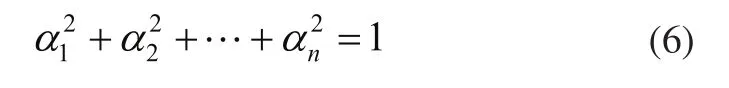
在U空間中：

在X空間中：

這里σi表示正態分布（或者是非正態分布的近似正態）的標準方差，可見靈敏度因子為確定性靈敏度和不確定性因素（方差）的函數。

圖5　二維情況下可靠性指標的定義

3.3概率分析軟件NESSUS介紹

NUSSUS是美國西南研究院為NASA專門研發的一款主要用于航天飛機發動機零部件失效概率分析以及風險評估的計算機軟件。后經過不斷發展，現NESSUS集成了隨機抽樣法、解析法、組合法以及替代法等四大類，17種概率計算方法；針對隨機變量，NESSUS提供17種概率密度分布函數，包括正態分布，威布爾分布，指數分布等。同時，NESSUS為用戶提供了廣泛的第三方接口，其可以與ANSYS、ABQUES、LS-DYNA等眾多的CAE軟件聯合使用。NESSUS聯合ANSYS進行可靠性計算的流程如圖6所示。

圖6　NESSUS聯合ANSYS工作流程

4　基于NESSUS的輪轂可靠性分析

4.1輪轂極限狀態方程的建立

考慮到輪轂極限工作載荷以及材料屬性參數的隨機性，將輪轂的工作載荷參數以及輪轂材料屬性參數（屈服強度σS、彈性模量Ex、泊松比Prxy及材料密度Density）都作為隨機變量引入到極限狀態方程中，根據應力-強度干涉模型建立輪轂的極限狀態方程如式（9）所示。

式中，f代表ANSYS有限元計算的函數；

S通過調用有限元求解的結果文件得到；

Mxi，Myi，Mzi，Fxi，Fyi，Fzi為輪轂載荷參數。

4.2各隨機變量分布參數的確定

輪轂載荷參數如表3所示。根據經驗，載荷參數的標準差取均值的8%，屈服強度Ex和泊松比Prxy的標準差均值的2%。屈服強度σS的標準差等于均值和輪轂材料的屈服強度變異系數的乘積，球墨鑄鐵的屈服強度變異系數為CS=0.04。由此可以得到輪轂各隨機變量的分布參數如表4所示，其中力矩的單位為kNm，力為kN，密度為kg/m3，強度為MPa。

表4　各隨機變量的分布參數

（續）

4.3概率分析方法的選擇

NESSUS提供包括蒙特卡洛法（MC）、一階矩法（FORM）、二階矩法（SORM）、均值法（MV）及其改進方法等17種概率分析方法，在此選用一階矩法（FORM）先進行計算，考慮到單種分析方式的計算誤差，在后面采用改進均值法（AMV）以及改進均值+法（AMV+）進行驗算，其中置信度設置為95%，取樣誤差設置為0.01。

4.4查看分析結果

利用一階矩法（FORM），改進均值法（AMV）以及改進均值+算法（AMV+）分別求得的輪轂的可靠度結果如表5所示。運用一階矩法（FORM）求得的輪轂的設計驗算點P在X（R，Mx1，…，Prxy， Density）空間的坐標以及設計點P處的單位法線的方向參數如表6所示，表6中力矩的單位為Nm，力為N，密度kg/ m3，強度為Pa，各隨機參數的靈敏度水平如圖7所示。

表5　可靠性指標結果

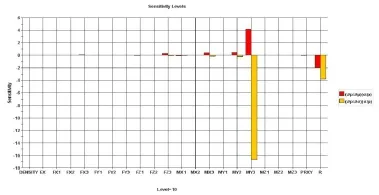
圖7　靈敏度水平結果

5　結論

輪轂的靜強度分析得到最大等效應力值為83.91MPa，其與安全系數的乘積小于輪轂的屈服強度，符合輪轂的強度要求。通過NESSUS聯合ANSYS對輪轂進行可靠性分析，得到該風機輪轂在極限工況下的可靠度指標為0.999996450，符合設計對輪轂可靠度的要求，對輪轂可靠性影響最大的兩個隨機變量分別是輪轂材料的屈服強度σS以及載荷參數My3，其余因素對輪轂的可靠度影響較小。對于屈服強度σS，靈敏度因子為=0.182，dPf/du1=-0.8449×10-12；對于載荷參數My3，靈敏度因子為=0.794，dPf/du20=0.3827× 10-10，可知屈服強度的均值增加會增加輪轂的可靠度，載荷參數My3的均值增加會降低輪轂的可靠度，這與實際情況相符。

表6　靈敏度分析結果

［1］ 吳佳梁，王廣良，魏振山.風力發電機可靠性工程［M］.北京：化學工業出版社，2010.

［2］ 鄭甲紅，杜翠.2MW風力發電機輪轂優化設計［J］.機械設計與制造，2011，（7）：7-9.

［3］ 張立剛.MW級風力發電機輪轂結構分析及優化方法的研究與應用［D］.重慶：重慶大學，2009.

［4］ 范光良，麥云飛，陳俞廷.大型風力發電機組輪轂強度分析［J］.制造業自動化，2012，34（16）：120-124.

［5］ 岳勇，謝建華，李振輝.復雜工況下風力機輪轂可靠性設計方法研究［J］.制造業自動化，2014，（2）：47-50.

［6］ 穆慧娜，張利敏，溫玉全，等.基于NESSUS的空氣隙傳爆界面可靠性分析［J］.北京理工大學學報，2013，33（4）：331-334.

［7］ 周新建，萬正平，周長國.基于NESSUS的汽車后橋可靠性靈敏度分析［J］.機械設計與制造，2009，（1）：68-70.

The reliability analysis of MW scale permanent magnet direct-drive wind generator's hub based on NEssUs

TM315

A

1009-0134（2016）08-0124-06

2016-06-22

永磁直驅風力發電機系統可靠性與維修性技術研究（20122BAB206027）

周新建（1963 -），男，教授，博士，研究方向為機械CAD/CAM和機械可靠性設計。