多元函數幾個概念的關系的研究

徐麗君，廖永志

多元函數幾個概念的關系的研究

徐麗君，廖永志

(攀枝花學院數學與計算機學院，四川攀枝花617000）

多元函數的連續性、可微性、偏導數、方向導數等概念比較抽象，關系復雜，是教學中的四大難點，難以理解，難以掌握。為了理清這些概念的內涵與關系，通過具體實例，充分利用有關概念與定理，詳細討論每一個概念的條件與結論之間的因果關系，以及這些基本概念之間的內在聯系，給高等數學的教學降低難度，讓初學者容易接受這些知識。

多元函數；關系；連續性；可微性；偏導數；方向導數

0 引言

高等數學是國家教育部規定的理工科經管類專業學生必學的一門課程，學習高等數學，不僅是在后續的課程的學習中將反復應用這些數學知識，更主要的是將會提高我們的邏輯思維能力，幫助學生養成嚴謹的治學態度，提高綜合素質。高等數學具有很強的抽象性，正是這一點使一些初學者有畏懼該課程的學習，缺乏自信，對一元函數的學習還好，多元函數的學習很困難，尤其對于多元函數的連續性、可微性、偏導數、方向導數幾個概念集中出現的時候，有些學生就把這些概念混淆了。本文將以實例為主，重點分析這幾個概念的內涵及其關系，希望能夠降低教學難度，減少讀者學習的抽象性。

1 幾個概念的定義和定理

下面給出函數的連續、可微、偏導數及方向導數的定義，以及顯示他們之間的關系定理，這是后面部分必須用的。

定義1[1]：設函數z=f（x，y）在區域D上有定義，點P0（x0，y0）∈D，若有成立，則稱函數z=f（z，y）在點P0處連續。

定義2[1]：設函數z=f（x，y）在點P0（x0，y0）附近有定義，固定y＝y0，當自變量x在x0處有增量△x時,函數z有相應的改變量f（x0+△x，y）-f（x0，y0）。如果

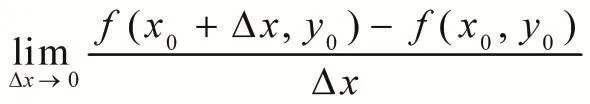
存在，則稱此極限為函數z=f（x，y）在點P0（x0，y0）處對x的偏導數。記為：P'x（x0，y0），z'x（x0，y0），

同樣,定義函數z=f（x，y）在點P0（x0，y0）對y的偏導數

定義3[1]：設z=（fx，y）在P（0x0，y0）的某鄰域內有定義，如果函數的全增量可表示為△z＝（fx0＋△x，y0＋△y）-f（x0，y0）=A△x+B△y+o(p)。其中，A與B是與△x和△y無關的常數，稱函數z=（fx，y）在點P0（x0，y0）可微，把△x，△y的線性函數A△x+B△y叫做函數z=（fx，y）在點P（0x0，y0）的全微分，記為：dz=A△x+ B△y。

定義4[1]：在點P（0x0，y0）的一條射線l上任取一點P（x0＋△x，y0＋△y），設，如果極限存在，稱此極限是函數z=（fx，y）在點P（0x0，y0）沿著l的方向導數，表示為，即

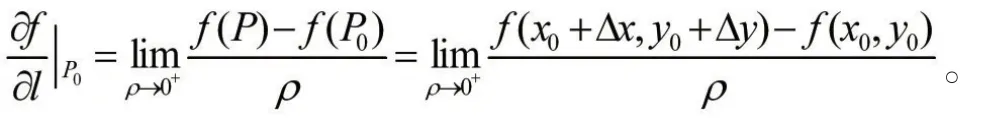
定理1[1]（可微的必要條件）：如果函數z=f（x，y）在點P0（x0，y0）可微，則在該點偏導數f'x（x0，y0），f'y（x0，y0）存在，且函數z=f（x，y）在點P0（x0，y0）全微分

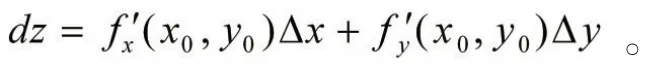
定理2[1]（可微的充分條件）：如果函數z=f（x，y）在點P0（x0，y0）的偏導數在點P0（x0，y0）處連續，則函數f（x，y）在點P0（x0，y0）有可微分。

定理3[1]：若函數z=f（x，y）在點P0（x0，y0）可微，則函數z=f（x，y）在該點沿任意方向l的方向導數都存其中cosα，cosβ是射線l的方向余弦。

2 幾個概念及其關系

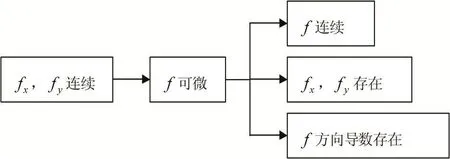
多元函數連續、可微、偏導數、方向導數四個概念比較抽象，要想弄明白它們之間的關系很不容易。具體來講“連續”表達的是函數的增量與每一個自變量的增量之間的關系，“偏導”表達的是函數變化率的問題，“微分”反應的是對函數的局部變化率的一種線性描述，“方向導數”體現了函數在某個射線方向上變化時對于距離的變化率，這四個問題共同點是求極限，不同點是求極限的內容不一樣，比如P(x,y)→P（x0，y0）的路徑不一樣，“連續”的路徑是任意方向，“偏導”的路徑是平行于x,y軸的直線方向，“微分”的路徑是P(x,y)→P（x0，y0）沒有方向，“方向導數”的路徑是射線方向。表面上看四個概念關系不大，但實質上相互之間關系相當密切。例如，關于x,y軸的正半軸的偏導數就是各自方向的方向導數，而關于x,y軸的負半軸的偏導數就是各自方向的方向導數的相反數。又如上面給出的3個定理可以充分反映他們之間的聯系，圖1形象地描述了這一點。

3 實例闡述

在上述關系中，反方向均不成立。下面取（x0，y0）=(0,0)點為例，充分利用定義1—定義4，定理1—定理3，從6個方面逐一討論函數的連續、可微、偏導數、方向導數四個概念之間的關系。

3.1 函數在某點偏導數存在，但不連續，不可微

解：因為f（x，0）=0，f（0，y）=0

即其偏導數存在。

當點P(x,y)沿x軸趨于點(0，0)時，有

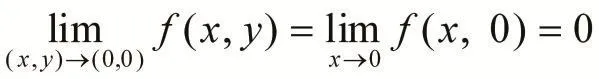
當點P(x,y)沿直線y＝kx趨于點(0，0)時，有

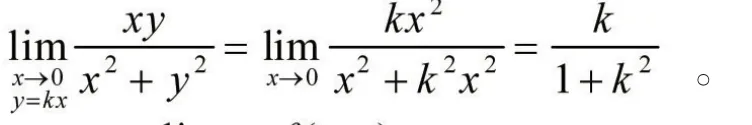
3.2 函數在某點連續，方向導數存在，但偏導數不存在，不可微

例2：求證：函數，在(0，0)點連續，方向導數存在，但偏導數不存在，不可微。

即該函數在（0，0）點存在方向數。但

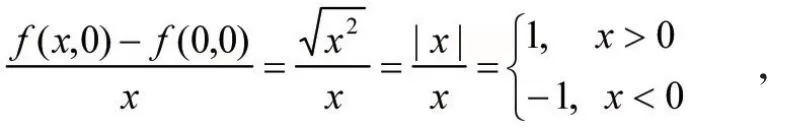
故，f（x0，0）不存在。由x，y的對稱性，f（y0，0）不存在。從而，（fx，y）在（0，0）點不可微（否則，f（x0，0），f（y0，0）均存在）。

3.3 函數在某點可微，但偏導數不連續

航保通信基建工程是在財政資金撥付下進行的固定資產投資項目建設，屬于公益性建設項目，本文所指的基建工程主要指基礎設施建設項目。財政資金撥付項目往往存在投資金額固定，建設周期短的問題，這就需要針對一些重點環境加強管理，以實現工程建設的高效推進。

因為，當x→0，y→0時，

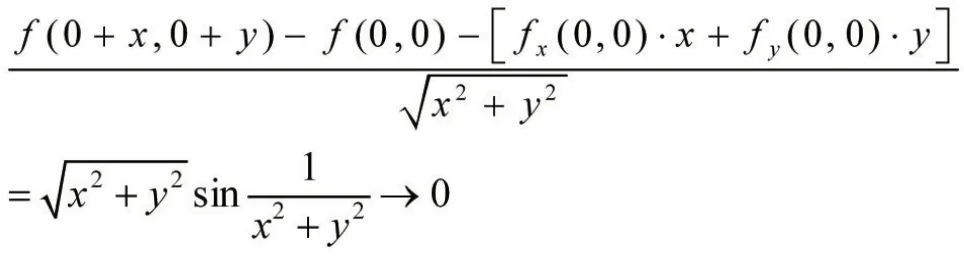
所以f（x，y）在（0，0）點可微，且df（0，0）=fx（0，0）dx+fy（0，0）dy=0

取點列Pn（xn，yn），yn=0，顯然。

這個例題也說明，上述定理1與定理2不可逆。

3.4 函數在某點連續，偏導數存在，但不可微

由定義

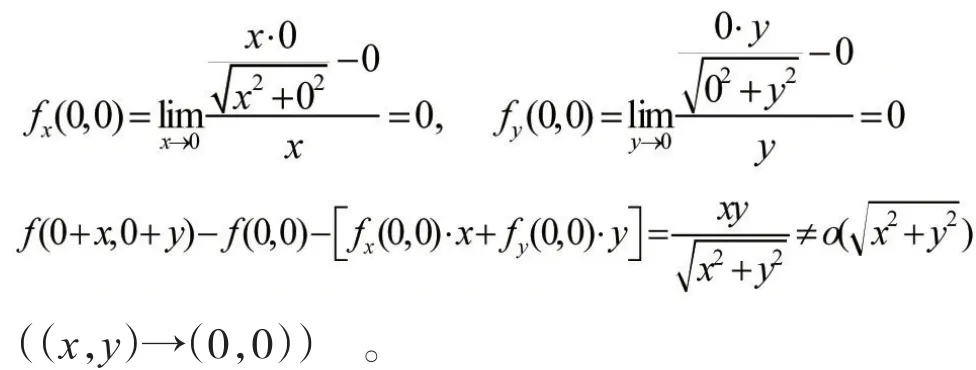
所以，函數f（x，y）在點（0，0）連續，偏導數存在，但不可微。

3.5 函數在某點的方向導數存在，但不連續，不可微

證明：函數沿方向l=（cosα，sinα）的方向導數為

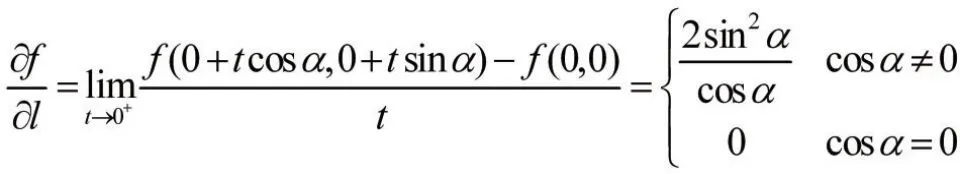
所以，函數在原點（0，0）處沿各個方向的方向導數存在。但當（x，y）沿曲線x=ky2趨于（0，0）時，又因為，此結果與k有關。所以，函數f（x，y）在原點（0，0）不連續，因而不可微。

3.6 函數在某點的方向導數存在，連續，但不可微

函數沿方向l=（cosα，sinα）的方向導數為

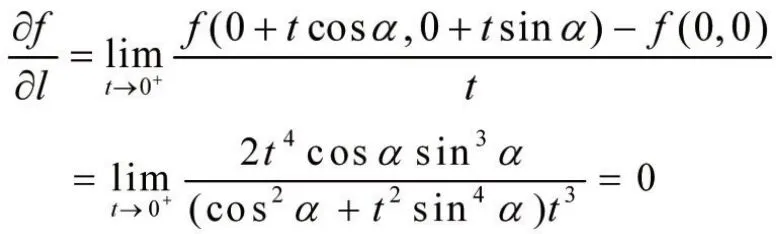
所以函數在原點（0，0）處沿各個方向的方向導數存在。又

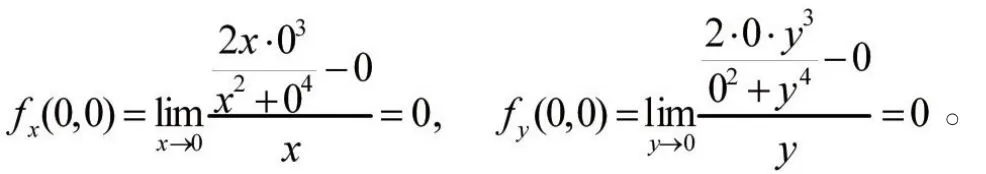
但因為

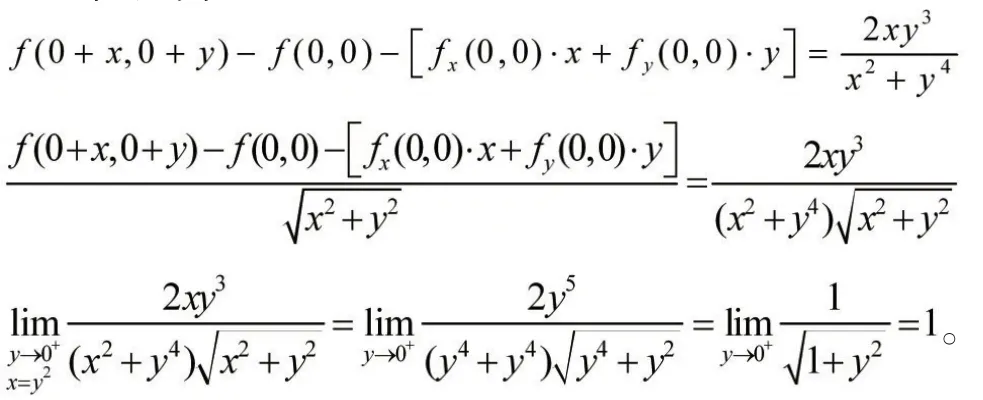
所以函數在原點（0，0）不可微。

4 結語

綜合上面的例子，說明函數的連續性、可微性、偏導數、方向導數等基本概念之間的關系復雜，特別抽象，極易混淆，難以理解，難以掌握。本文以具體實例為主，詳細研究這些概念之間的內在關系，得到下面的“結論圖”，這個圖可以給高等數學的教學降低難度，可以讓初學者能夠容易理清這些概念的內涵，從而學好高等數學這門課程。

[1]華東師范大學數學系.數學分析[M].北京：高等教育出版社，2004．

[2]同濟大學應用數學系.高等數學[M].北京：高等教育出版社，2005．

[3]陳紀修．數學分析[M].北京：高等教育出版社，2006．

The Study on the Connection of Several Concepts of Multivariate Function

XU Li-jun，LIAO Yong-zhi
(School of Computer Science and Technology，Panzhihua University，Panzhihua,Sichuan 617000,China)

The concept of multiple functions,such as continuity,differentiable,partial derivative,directional derivative,is abstract and complex.They are the four special difficulties in teaching.In order to comprehend the connotation and concept of them,through concrete examples,we make full use of the concepts and theorems,and discuss in detail the causal connection between the conditions and conclusions of each concept,and the inner link between these basic concepts,which reduce the difficulty of teaching higher mathematics,which help beginners accept these knowledge easily.

multivariate function;connection;continuity;differentiability;partial derivative;directional derivative.

O174.1

A

1673-1891（2016）01-0023-03

10.16104/j.issn.1673-1891.2016.01.007

2015-11-01

徐麗君（1965—），女，副教授，學士，研究方向：微分方程。