立體幾何中的探索開放型的解法

◇　山東　王世雙(特級教師)

?

重點輔導

立體幾何中的探索開放型的解法

◇山東王世雙(特級教師)

所謂探索開放型題是相對于有明確條件和明確結論的封閉型問題而言的．開放型問題在立體幾何的試題中常見的形式有以下幾種.

1結論探索型

給出條件,沒有給出明確結論(或者結論不唯一)的問題,需要解題者探索出結論,并加以證明.

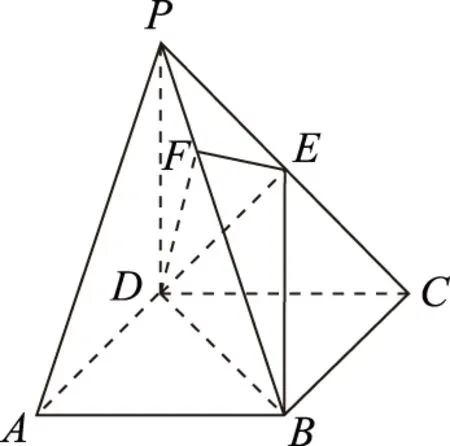
圖1

(1) 證明:PB⊥面DEF. 試判斷四面體DBEF是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;

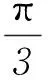
因為PD=CD,點E是PC的中點,所以DE⊥PC.而PC∩BC=C,所以DE⊥平面PBC. 而PB?平面PBC,所以PB⊥DE.

又PB⊥EF,DE∩EF=E,所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF,可知四面體BDEF的4個面都是直角三角形,即四面體BDEF是一個鱉臑,其4個面的直角分別為∠DEB、∠DEF、∠EFB、∠DFB.

圖2

(2) 如圖2所示,在面PBC內,延長BC與FE交于點G,則DG是平面DEF與平面ABCD的交線. 由(1)知,PB⊥平面DEF,所以PB⊥DG.

又因為PD⊥底面ABCD,所以PD⊥DG. 而PD∩PB=P,所以DG⊥平面PBD.故∠BDF是面DEF與面ABCD所成二面角的平面角.

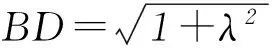
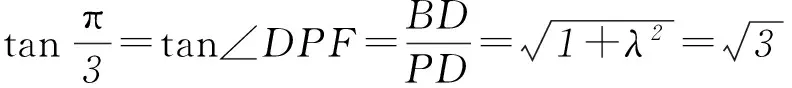
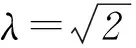
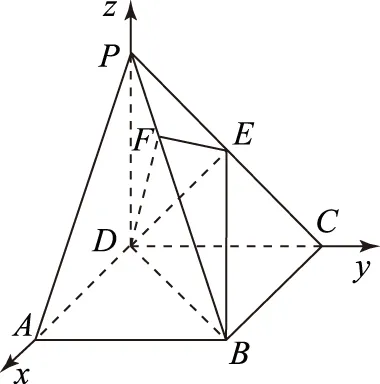
圖3

解法2坐標法.

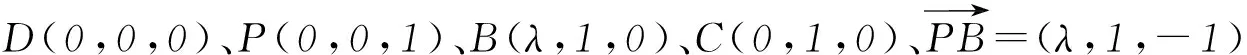
又已知EF⊥PB,而DE∩EF=E,所以PB⊥平面DEF.

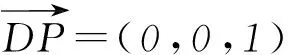
2條件探究型

給出結論,沒有給出條件的問題,要解題者分析出應具備的條件,并加以證明.

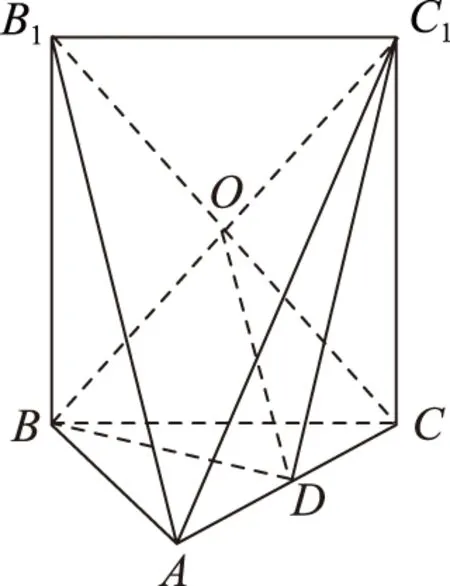
圖4

3“是否存在”型

此種題型的解法常常從最簡單、最特殊的情況出發．有時也可借助直覺觀察或判斷,推測出命題的結論,必要時給出嚴格證明;有時需逆向思維尋找思路．

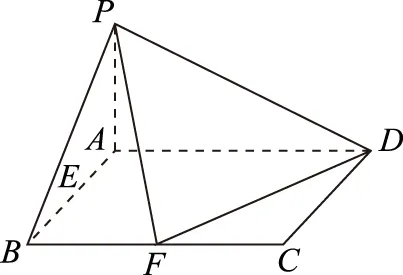
圖5

(1) 證明:PF⊥FD;

(2) 判斷并說明PA上是否存在點G,使得EG∥平面PFD;

(3) 若PB與平面ABCD所成的角為45°,求二面角A-PD-F的余弦值.

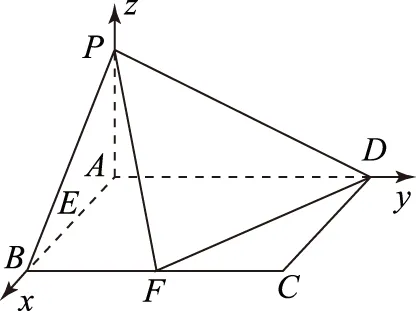
圖6

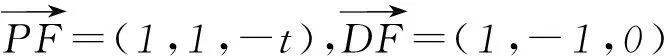
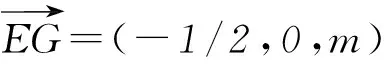
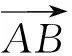
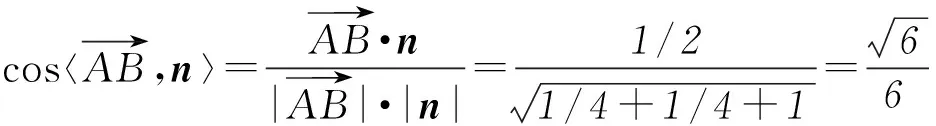
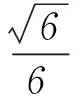
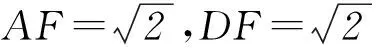
又PA⊥平面ABCD,所以DF⊥PA.又PA∩AF=A,所以DF⊥平面PAF,又PF?平面PAF，所以DF⊥PF.

圖7

(3) 因為PA⊥平面ABCD,所以∠PBA是PB與平面ABCD所成的角,即∠PBA=45°，故PA=AB=1.如圖7所示，取AD的中點M,則FM⊥AD,FM⊥平面PAD,在平面PAD中,過M作MN⊥PD于N,連接FN,則PD⊥平面FMN,則∠MNF即為二面角A-PD-F的平面角.

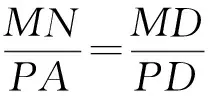
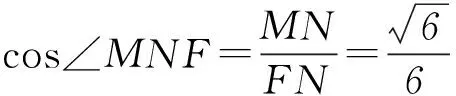
探索型問題取材廣泛,形式活潑,涵蓋知識面廣,解題方法靈活,需要同學們在觀察、猜想、推理、論證、總結、歸納、實踐、創新等方面多加強練習,從而提升數學能力．

(作者單位：山東省淄博第五中學)