關于一道函數題的初步探討
2016-07-28 06:36:30山東藝璇北京童嘉森特級教師
高中數理化 2016年7期
關鍵詞:性質
◇ 山東 藝璇 北京 童嘉森(特級教師)
?
童嘉森數學之窗
關于一道函數題的初步探討
◇山東藝璇1北京童嘉森2(特級教師)

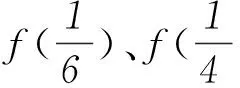

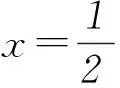
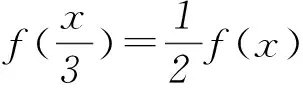
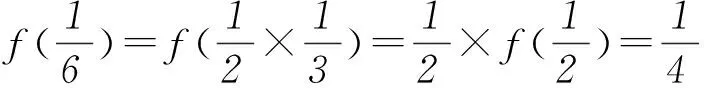
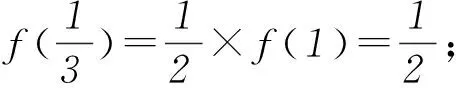
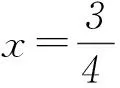
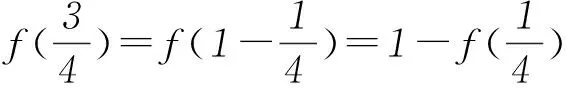
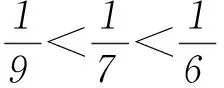
當采集一個信號后,通過控制系統直接數字頻率合成,輸出與該頻率相關的信號,然而輸入和輸出信號間的相位差是可控的.從聲場的線性疊加原理可知,頻率相同、同向傳播的兩列聲波會在空間中產生相加或者相消的干涉現象,干涉后的波峰波谷,完全取決于兩列聲波的相位和幅值的關系[11-12].
解答完該題后,不妨研究一下這個函數.由于f(x)是非減函數,并且具有題設的3條性質,在此我們嘗試對函數f(x)的性質作進一步探討.
1函數f(x)的對稱性
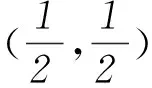
2函數f(x)部分特殊點的通項公式
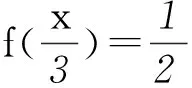
……
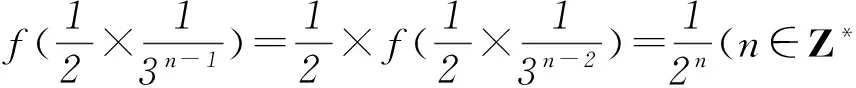
同時還有:
……
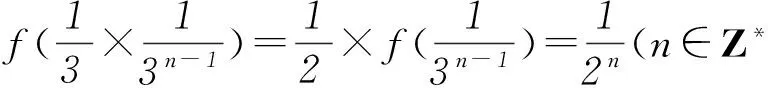
同時,能夠得出
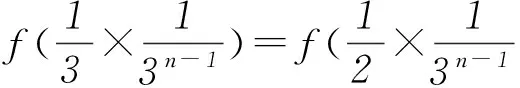
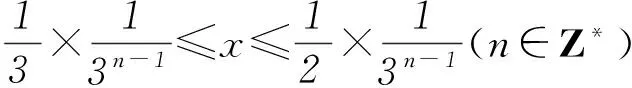

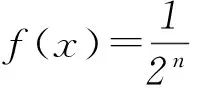
按照這個思路繼續推算下去,我們發現:
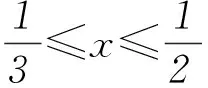
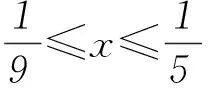
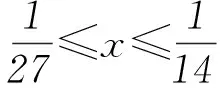
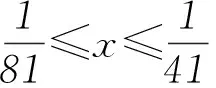
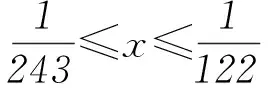
……
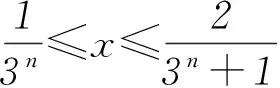
3函數f(x)的不連續性及大致圖象
根據函數f(x)部分特殊點的通項公式以及計算過程可以看出,任意一個位于區間[0,1]上的有理數都可由性質②、③和非減函數的特性求出對應的函數值. 而對于無理數來說,雖然部分無理數能通過比較相鄰2個有理數的大小,來求出對應的函數值,但存在部分無理數,無法根據題設性質求得函數值.因此,函數f(x)是不連續的. 對于這一結論,我們可以通過反證法證明.
假設對于任意無理數x0∈[0,1],都能由題設條件求得唯一確定的函數值f(x0)與之對應.因為無理數無法借助性質②、③求值,那么必然存在與x0接近的2個有理數x1、x2(x1< x0 但是我們為了能夠初步了解函數f(x)的上述性質,不妨作出其大致的圖象(圖1). 圖1 (作者單位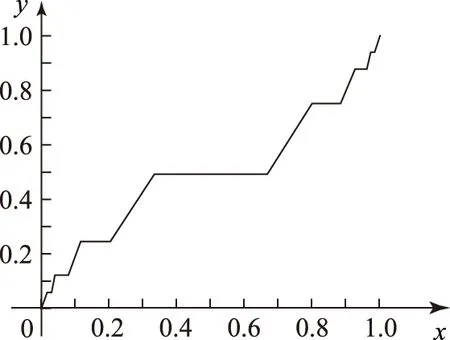
猜你喜歡
中學生數理化·高三版(2023年6期)2023-07-19 11:17:53
數學物理學報(2022年6期)2022-12-15 08:45:02
上海師范大學學報·自然科學版(2022年3期)2022-07-11 03:05:59
數學雜志(2021年6期)2021-11-24 11:12:00
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
數學年刊A輯(中文版)(2021年1期)2021-06-09 09:31:56
中等數學(2020年6期)2020-09-21 09:32:38
山東農業工程學院學報(2019年11期)2020-01-19 02:49:10
數學物理學報(2019年6期)2020-01-13 06:07:52
中等數學(2019年6期)2019-08-30 03:41:46

