隔震結構損傷性能與可靠度研究

杜東升， 王曙光， 劉偉慶， 李威威

(南京工業大學 土木工程學院，南京　210009)

?

隔震結構損傷性能與可靠度研究

杜東升， 王曙光， 劉偉慶， 李威威

(南京工業大學 土木工程學院，南京210009)

摘要：提出隔震結構的地震損傷模型，并采用概率密度演化理論分析隔震結構地震損傷指數的概率統計特征，為隔震結構性態目標的量化提供依據。考慮隔震支座的壓剪相關性和拉壓性能的差異，給出隔震層的損傷指數模型，再利用Park-Ang損傷指數描述上部結構的損傷狀況，建立隔震體系的損傷指數模型；將隔震結構簡化為雙質點模型，采用Bouc-Wen模型和剛度退化的Bouc-Wen模型分別描述隔震層與上部樓層的滯變特性，建立隔震結構的狀態方程，應用四階龍格-庫塔法迭代求解出隔震結構的位移反應和滯變耗能，進而求解隔震結構的損傷指數；建立隔震結構損傷指數的概率密度演化方程，求解損傷指數的統計特征和概率密度函數，然后根據極值分布理論計算損傷指數超過不同性能水準的可靠度。該研究為以可靠度為理論基礎的隔震結構損傷分析提供可借鑒的方法。

關鍵詞：可靠度；隔震結構；損傷指數

隔震結構在超烈度地震作用下可能會遭受一定程度的損傷，如何評價其損傷程度，特別是隔震層的損傷程度，是工程抗震和結構振動控制領域內一個重要問題，另外由于地震動的隨機性隔震結構的損傷必然會存在明顯的概率特征，因此研究隔震結構的損傷模型并對其進行可靠度評價將對隔震結構的推廣具有重要意義。

在結構基于性態的抗震設計研究中，損傷是性態目標量化的一個主要研究內容，常規結構的地震損傷目前很多學者傾向于采用Park和Ang[1]提出的損傷指數模型，該模型具有較好的試驗基礎，形式表達簡潔，是基于規格化最大位移和規格化滯回耗能線性組合的雙參數模型，可以近似反應構件的位移首次超越和塑性累計損傷聯合作用的地震破機理，因此該模型提出以后得到了工程抗震領域的廣泛認同和應用。但該模型未將結構損傷和加載路徑相關聯，且存在上下界不收斂的問題[2]，所以該模型與一些擬靜力試驗結果吻合不理想[3]，因此很多學者[4-6]都對該模型進行了修正和改進。Park-Ang地震損傷模型是針對鋼筋混凝土構件提出的，對于隔震結構的上部結構仍然適用，但是無法適用于隔震層的損傷描述，隔震層的損傷和失效必須要考慮隔震支座的剪壓相關性，并且豎向受拉損傷是隔震層損傷描述必須要考慮的內容，提出隔震層的損傷模型是對隔震結構進行地震損傷研究的必要條件。

隔震結構的地震損傷模型是對其進行性態目標量化的基礎，而損傷指數由于地震作用的隨機性必然會有明顯的概率特征，在計算隔震結構的地震響應和損傷時確定性地震動輸入很難把握結構隨機地震響應全面精細的信息，從而很難對隔震結構的性態進行全面有效的把握與控制。因此很多學者將隨機分析方法引入到隔震結構分析中去，隔震結構是一種典型的非線性結構體系，瞿偉廉等[7]根據隨機最優控制理論提出了將隔震結構地震反應控制在彈性范圍內的設計計算方法，但該方法無法適用于隔震結構在罕遇地震下的性能評價；杜永峰等[8]將隔震結構進行等效線性化處理，并采用虛擬激勵法計算了隔震結構的平穩地震響應和動力可靠度；李杰等[9]提出和發展了概率密度演化方法，該方法很好的解決了非線性結構的非平穩隨機地震反應，利用該方法，彭勇波等[10]對隔震結構的非平穩地震反應和動力可靠度進行了系統的研究。這些研究都是對結構的隨機地震反應進行分析，很少涉及到結構的隨機損傷和損傷可靠度的研究。

本文以Park-Ang地震損傷模型的基本思想為基礎，考慮隔震層的剪壓相關性和隔震支座拉壓的差異性，提出適合隔震層的地震損傷模型，并采用概率密度演化理論研究隔震結構的隨機損傷和損傷可靠度。本研究為以可靠度為理論基礎的隔震結構損傷分析提供了可借鑒的方法。

1隔震結構損傷模型

目前對結構地震損傷的研究主要是綜合考慮結構的最大位移響應和塑性累積損傷，1985年Park和Ang提出的地震彈塑性變形和累積滯變耗能線性組合的地震損傷模型比較符合結構在罕遇地震作用下的損傷情況，其可以表示為：

(1)

式中：Di為地震作用下結構第i層的損傷指數，δmaxi為地震下結構第i層的最大位移；δui為單調加載下結構第i層的極限變形；Qyi為結構第i層的屈服強度；∑Ei為結構第i層的累計滯回耗能；β為一非負常數，根據Bertero等[11]的建議本文取0.2。該模型也是適用于隔震結構上部各層的損傷量化，但對于隔震層，該模型是無法反映其壓剪相關性對隔震層損傷的影響，也無法反映隔震支座拉壓特性的差異及支座的受拉損傷，而這兩個方面是影響隔震層損傷必須考慮的，綜合隔震層彈塑性變形和累積滯變耗能，提出隔震層的損傷模型：

對于隔震結構整體損傷指數模型，可以采用加權平均值法建立的整體結構的損傷模型：

(3)

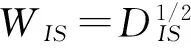
2隔震結構損傷響應

隔震層的滯變恢復力模型是建立隔震結構振動控制方程的關鍵因素，Bouc于1967年首先提出用微分方程描述光滑滯變恢復力過程，后Wen等又提出了光滑滯變位移的微分方程，式(4)給出了Bouc-Wen模型的表達式：

(4)

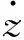
式中：Al、ν和η均是累積滯變耗能的函數，并根據滯回耗能確定結構退化的程度。

根據隔震結構的特點，可以采用Bouc-Wen模型描述隔震層的滯變特性，用剛度退化的Bouc-Wen模型描述部樓層的滯變特性，從而可以建立隔震結構的振動控制方程：

(6)

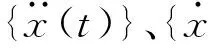
式中：kb、αb分別為隔震層一次剛度和二次剛度系數，k1～kj、α1～αj分別為上部各層的一次剛度和二次剛度系數。為了求解方程(6)，將位移、速度和滯變位移共同形成狀態空間，建立隔震結構狀態方程：

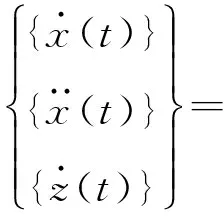
(7)

式(7)可以簡寫為：

(8)

采用四階龍格-庫塔方法求解上述狀態方程，可以得出隔震結構的地震反應和滯回耗能，將計算結果代入方程(2)和方程(3)即可以求解出隔震結構的損傷指數隨時間變化的情況。圖1給出了隔震結構和非隔震結構在202條地震波作用下各層及整體的損傷指數，可以看出，隔震結構的整體損傷指數最大0.47，遠小于非隔震結構的1.92，從損傷的角度也說明隔震結構在具有較好的抗震性能，另外也可以看出，對應于非隔震結構，隔震結構上部結構的損傷指數都很小，結構整體的損傷指數受隔震層損傷指數的影響較大。另外需要說明的是非隔震結構的損傷指數都超過了認為倒塌的0.8，主要是由于該模型損傷指數的最大值不收斂造成的。

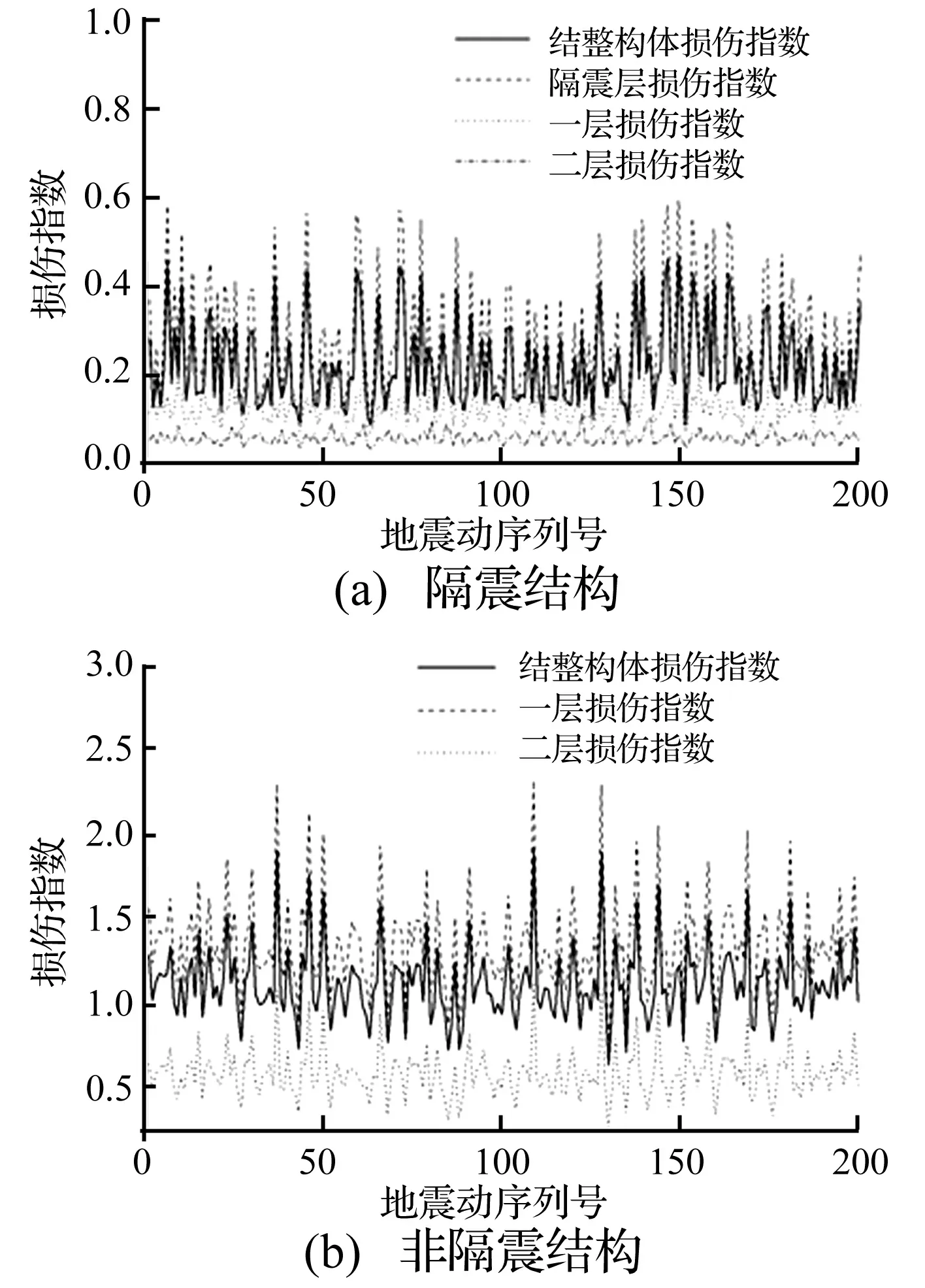
圖1　隔震結構和非隔震結構的損傷指數Fig.1 Damage index of base isolated structure and base non-isolated structure

圖2給出了隔震結構在不同地震動作用下整體損傷指數、隔震層及上部結構損傷指數隨時間的變化曲線。可以看出隔震結構的整體損傷指數受到壓剪和塑性累計損傷的共同影響，呈波動逐漸增加的趨勢，而上部結構由于塑性累計損傷很小，損傷指數主要受位移超越的影響而僅隨時間波動，且損傷指數遠小于隔震層，說明隔震結構的隔震層是容易首先損傷失效的部位。另外從圖2(a)可以看出，不同地震動作用下隔震結構的損傷指數離散性較大，這與地震動幅頻特性和時頻特性的差異有很大關系。

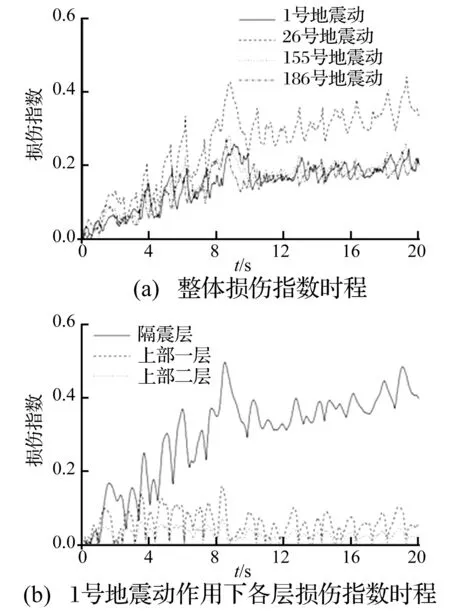
圖2　隔震結構損傷指數時程Fig.2 Time history ofdamage index of base isolated structure

3隔震結構損傷指數的概率密度演化

隔震結構的地震損傷模型是對其進行性態目標量化的基礎，而損傷指數由于地震作用的隨機性必然會有明顯的概率特征，目前雖然對結構隨機地震反應已經進行了大量的研究，但對于非線性結構的隨機反應的解答仍存在一定困難。2008年，李杰、陳建兵將概率密度演化方法與物理隨機地震動模型相結合，從概率密度演化的基本思想出發，建立廣義概率密度演化方程，在線性與非線性多自由度結構系統的隨機反應分析、動力可靠度和體系可靠度計算以及基于可靠度的結構控制方面能進行較為廣闊的應用。

采用概率密度演化方法同樣也可以分析隔震結構損傷指數的概率密度演化過程，首先仍然是選取離散的代表點，考慮地震動的隨機性，選用基底譜幅值、場地基本圓頻率以及場地等價阻尼比三個參數作為隨機變量，然后合成具有概率意義的多條人工地震動，并利用其進行隔震結構的損傷響應的計算，得到具有概率意義的損傷響應時程，如圖1所示，然后再利用下式對其進行微分：

(10)

將式(10)代入到概率密度演化方程中：

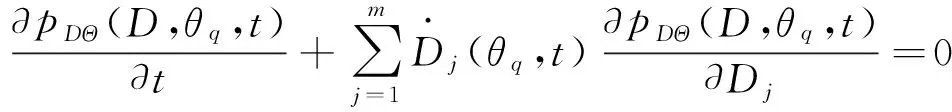
q=1,2,…,nsel

(11)

采用有限差分法的LW或TVD格式求解該偏微分方程，將上述求得的pDΘ(D,θq,t),q=1, 2, …,nsel累計求和，即得到隔震結構損傷指數的的概率密度函數PD(D,t)的數值解。

(12)

圖3給出了隔震結構整體和各層損傷指數的均值與標準差隨時間變化的過程，從圖中可以看出，整體和各層損傷指數的均值與標準差隨時間的變化規律基本同步，上部結構的損傷明顯小于隔震層。由于地震動的強隨機性造成了損傷指數的不確定性，隔震層損傷指數的離散性較上部結構大很多，而且隨著時間和損傷程度的增加損傷響應的離散性增加。

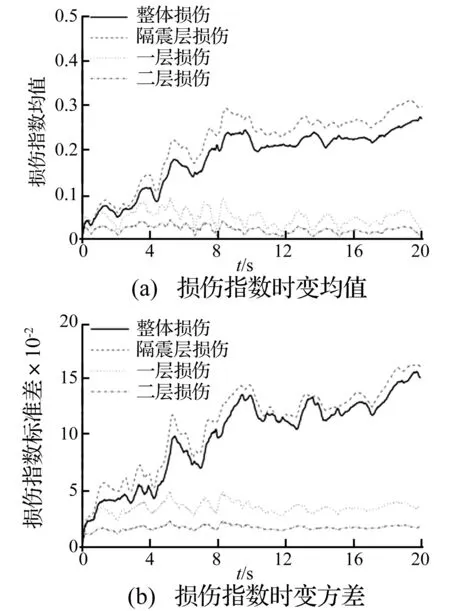
圖3　隔震結構損傷指數的時變均值與標準差Fig.3 Time-varying average and standard deviation of damage index of base isolated structure

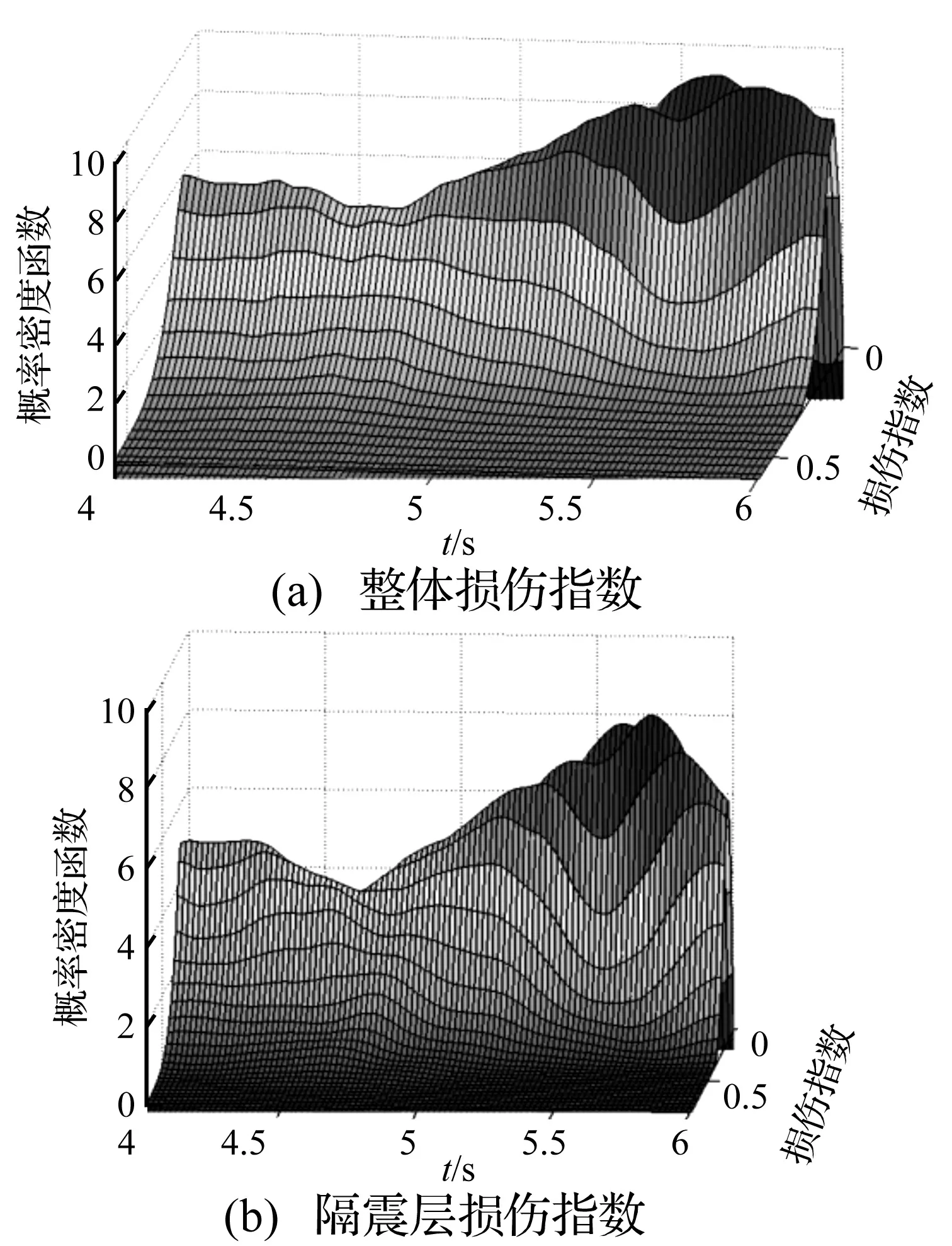
圖4　隔震結構損傷指數的概率密度演化曲面Fig.4 Probability density evolution curved surface of damage index of base isolated structure

圖4和圖5給出了隔震結構整體損傷指數和隔震層損傷指數的概率密度函數演化曲面和概率密度等值線，可以看出損傷指數的概率密度函數及其隨時間的演化過程與通常假定的正態分布等規則分布不同，其概率分布是非規則曲線，這也是概率在狀態空間中流動的結果。從圖中也可以看出，隔震結構整體的損傷指數的概率密度演化規律主要受隔震層損傷指數概率密度演化規律的影響，另外隔震結構整體損傷指數的概率分布基本上集中在0.3以內，而隔震層損傷指數的概率分布集中在0.4以內，這樣精細化的結論能為隔震結構的性態評估和設計提供充分的依據。

圖5　隔震結構損傷指數的概率密度等值線Fig.5 Probability density isoline of damage index of base isolated structure

4基于極值分布的隔震結構損傷可靠度

基于跨越過程理論的方法是計算結構可靠度應用最為廣泛的方法，但由于要對跨越事件的性質需要進行假定，會使得基于跨越過程理論計算的結構動力可靠度的分析精度又難以確保[13]。李杰等[14]基于隨機結構動力反應概率密度演化的思想，提出了施加吸收邊界條件進行結構動力可靠度分析的概率密度演化方法，在得到反應量的極大值分布之后直接積分給出結構的動力可靠度。

該方法同樣可以應用于隔震結構損傷的可靠度分析中，構造一個虛擬的隨機過程，使得隔震結構隨機損傷的極值為該虛擬隨機過程的截口隨機變量，建立概率密度演化方程并求解給出隔震結構損傷指數的極值概率分布，并在安全域內積分給出隔震結構損傷的動力可靠度。求出隔震結構各層損傷指數的概率密度函數PD(D)后，各層損傷指數的動力可靠度為：

(13)

圖6給出了隔震結構損傷指數的極值概率分布，其中6(a)圖給出了整體結構損傷指數按照概率密度演化方法和假定損傷指數服從正態分布得到的概率分布曲線，可以看出二者在損傷指數較小時差別較大。圖6(b)圖給出了整體結構、隔震層和上部樓層損傷指數的極值概率分布曲線，可以看出，隔震結構損傷指數的可靠度主要受隔震層損傷指數可靠度的影響，上部結構損傷指數的可靠度遠遠小于隔震層，所以提高隔震層的可靠度是提高隔震結構可靠度的主要途徑。

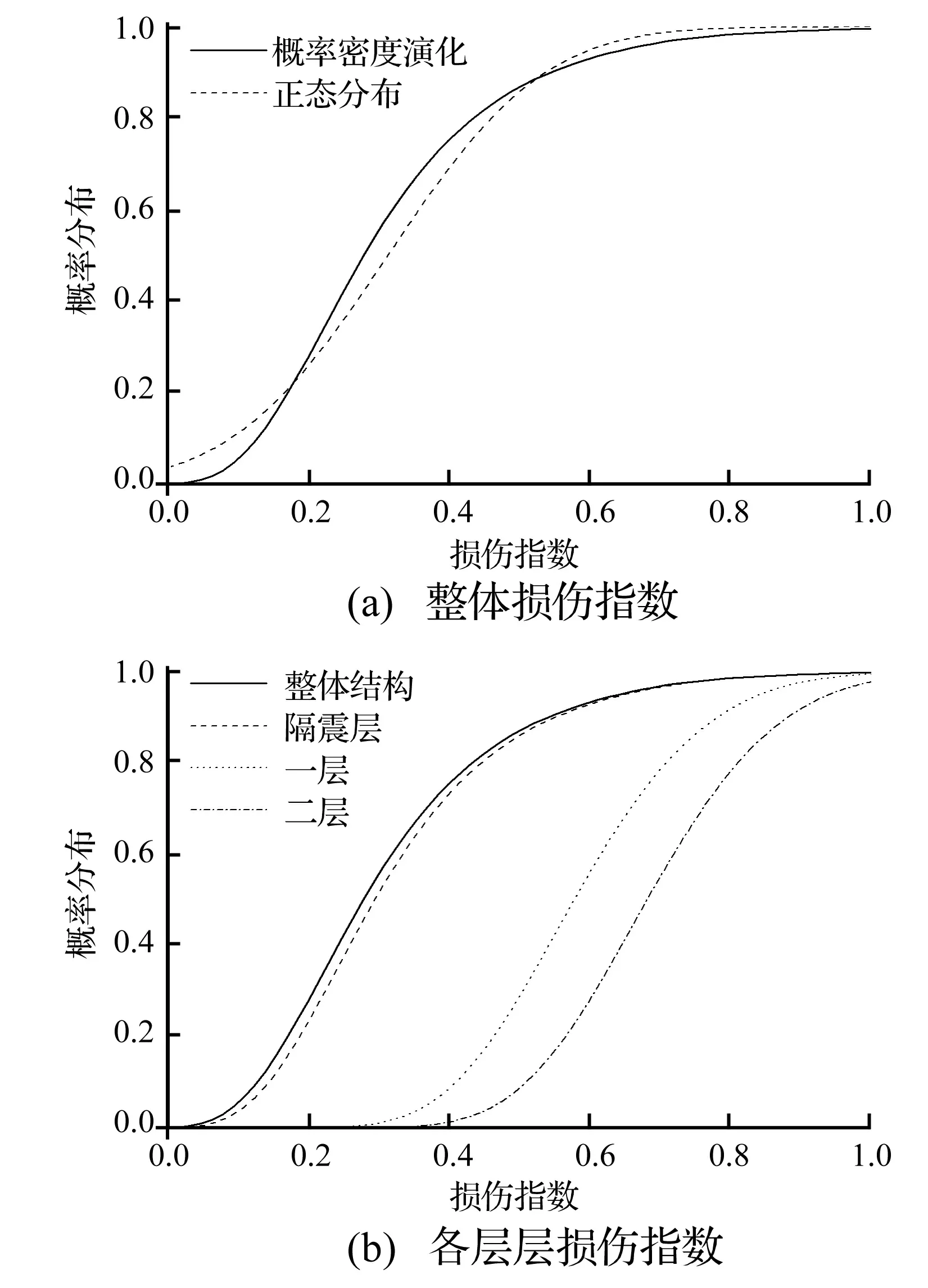
圖6　隔震結構損傷指數的極值概率分布Fig.6 Probability distribution of the largest value of damage index of base isolated structure

5結論

本文提出隔震結構的地震損傷模型，并采用概率密度演化理論分析了隔震結構地震損傷指數的概率統計特征，主要得到如下結論：隔震層上部結構的損傷指數較非隔震結構小很多，結構整體的損傷指數受隔震層損傷指數的影響較大；地震動的隨機性造成了損傷指數的不確定性，損傷指數的離散性隔震層較上部結構大很多；隔震結構整體損傷指數的概率密度演化規律和可靠度主要受隔震層特性的影響，隔震層上部結構損傷指數的可靠度遠遠小于隔震層，提高隔震層的可靠度是提高隔震結構可靠度的有效途徑。

參 考 文 獻

[1] Park Y J, Ang A H S. Mechanistic seismic damage model for reinforce concrete[J]. Journal of Structural Engineering, ASCE, 1985, 111(4): 722-739.

[2] Bozorgnia Y, Bertem V V. Damage spectra characteristics and applications to seismic reduction[J]. Journal of Structural Engineering, 2003,129(10):1330-1332.

[3] Chai Y H,Romstall K M, Bird S M. Energy-based linear damage model for high-intensity seismic loading[J]. Journal of Structural Engineering, 1995,121(5): 857-858.

[4] 王東升，司炳君，艾慶華，等. 改進的Park-Ang地震損傷模型及其比較[J]．工程抗震與加固改造，2005，27(增刊1):138-143.

WANG Dong-sheng, SI Bing-jun,AI Qing-hua,et al．A comparative study of modified Park-Ang model and park-ang model for structural seismic damage evaluation[J]. Earthquake Resistant Engineering Retrofitting, 2005，27(Sup1):138-143.

[5] 陳林之，蔣歡軍，呂西林，等. 修正的鋼筋混凝土結構Park-Ang損傷模型[J]. 同濟大學學報:自然科學版，2010，38(8): 1103-1107.

CHEN Lin-zhi, JIANG Huan-jun, Lü Xi-lin. Modified Park-Ang damage model for reinforced concrete structures[J]. Journal of Tongjiun 2versii’y:Natural Science, 2010，38(8): 1103-1107．

[6] Park S W,Wen W P,Cooper J D,et al. A comparative study of US-Japan seismic; design of highway bridges:II. shake table model tests[ J].Earthquake Spectra, 2003, 19(4):933-958.

[7] 瞿偉廉，陶牟華，李桂青． 基底滯后隔震層對建筑結構隨機地震反應的控制[J]． 應用力學學報，1989，6(3): 69-78．

QU Wei-lian，TAO Mou-hua，LI Gui-qing． Control for earthquake responses of architectural structures with hysteresis isolation systems in base[J]． Chinese Journal of Applied Mechanics，1989，6(3): 69-78.

[8] 杜永峰，張恩海，李慧，等． 隔震結構“小震不壞”的動力可靠度分析[J]． 地震工程與工程振動，2006，24(5): 84-89．

DU Yong-feng，ZHANG En-hai，LI Hui，et al． Dynamic reliability of isolated structure for “undamaged under minor earthquake”[J]．Earthquake Engineering and Engineering Vibration，2006，24(5): 84-89.

[9] 李杰，陳建兵． 隨機振動理論與應用新進展[M]．上海: 同濟大學出版社，2009: 60-94．

[10] 彭勇波，陳建兵，劉偉慶，等． 隔震結構的隨機地震反應與抗震可靠度評價[J]． 同濟大學學報，2008，36(11): 1457-1461.

PENG Yong-bo， CHEN Jian-bing， LIU Wei-qing， et al． Stochastic seismic response and aseismic reliability assessment of baseisolated structure[J]． Journal of Tongji University，2008，36(11): 1457-1461.

[11] Bertero R D, Bertero V V. Performance-based seismic engineering: the need for a reliable conceptual comprehensive approach [J]. Earthquake Engineering and Structural Dynamics,2002, 31(3): 627-52.

[12] 歐進萍，王光遠． 結構隨機振動[M]．北京: 高等教育出版社，1998: 295-301.

[13] 陳建兵, 李杰. 隨機結構動力可靠度分析的極值概率密度方法[J]. 地震工程與工程振動, 2004, 24(6): 39-44.CHEN Jian-bing, LI Jie. The extreme value probability density function based method for dynamic reliability assessment of stochastic structures[J]. Earthquake Engineering and Engineering Vibration，2004, 24(6): 39-44.

[14] 陳建兵, 李杰. 結構動力隨機反應的極值分布[J]. 福州大學學報:自然科學版, 2005, 33(增刊1): 11-15.

CHEN Jian-bing, LI Jie. The extreme value distribution of dynamic stochastic response of structures[J]. Journal of Fuzhou University:Natural Science，2005, 33(Sup1): 11-15.

基金項目：江蘇省前瞻性聯合研究項目(BY2015005-14)；國家自然科學基金(51178219)

收稿日期：2014-02-01修改稿收到日期：2015-09-06

通信作者王曙光 男，教授，博士生導師，1972年生

中圖分類號:TU311.3

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2016.01.035

Reliability-based damage performance of base-isolated structures

DU Dong-sheng, WANG Shu-guang, LIU Wei-qing, LI Wei-wei

(College of Civil Engineering, Nanjing University of Technology, Nanjing 210009, China)

Abstract:The seismic damage model of base-isolated structures was proposed. The stochastic characteristics of damage index of base-isolated structures were analyzed with the probability density evolution method. This study provided a basis for performance objective quantification of base-isolated structures. The damage index model of the isolation story was proposed considering the compression-shear correlation and tension-compression difference of isolators. The Park-Ang damage index was used to describe damage status of the superstructure, then the damage index model of base-isolated structures was established, and the simplified two-mass calculation model of base-isolated structures was established. Bouc-Wen model was used to simulate the isolation layer and Bouc-Wen model with stiffness degradation was used to simulate the superstructure, and the state equation of base-isolated structures was established. The displacement response and the hysteretically dissipated energy of base-isolated structures were iteratively solved with the fourth-order Runge-Kutta method. As a result, the damage index of base-isolated structures then was solved. The probability density evolution equation of base-isolated structures was established. The stochastic characteristics and probability density function of the damage index were solved. The reliabilities of the damage index not exceeding different performance levels were calculated with the extreme value distribution theory. The reliabilities of base-isolated structures affected by different yield force ratios and period ratios were also analyzed. This study provided a reference method for performance-based aseismic design of base-isolated structures on basis of the reliability theory.

Key words:reliability; base-isolated structure; damage index

第一作者 杜東升 男，博士，副教授，1977年生