變分模態分解在軸承故障診斷中的應用
岳應娟,孫鋼,蔡艷平,劉長江,張世雄
(第二炮兵工程學院,西安 710025)
軸承振動信號具有非線性、非平穩的特性,傳統的信號分析方法難以處理,經驗模態分解(Empirical Mode Decomposition,EMD)[1-5]能夠較好地處理此類信號,但也存在端點效應、包絡擬合及模態混疊等問題[6-9],仍需進一步優化。
變分模態分解(Variational Mode Decomposition,VMD)[10]是一種新的自適應信號處理方法,其本質上是多個自適應維納濾波組,有著良好的噪聲魯棒性。VMD可實現信號頻域內各個分量的自適應剖分,有效克服EMD算法分解過程中的模態混疊及偽分量等不足,比EMD有更強的噪聲魯棒性及較小的端點效應。因此,嘗試將VMD與譜峭度相結合,用于軸承故障信號的診斷。
1 變分模態分解算法
VMD通過迭代搜尋變分模型的最優解來確定每個本征模態分量(Intrinsic Mode Function, IMF)的中心頻率和帶寬,實現信號頻域和各個IMF的自適應剖分,是一種完全非遞歸的信號分解方法。
信號經過VMD處理被分解成一系列IMF,每個IMF都可以表示為一個調幅-調頻uk(t)信號,表達式為
uk(t)=Ak(t)cos(φk(t)) ,
(1)
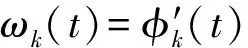
為估算每個IMF的帶寬,可分3個步驟:1)通過 Hilbert 變換計算與每一個模態uk(t)相關的解析信號;2)通過加入指數項調整各自估計的中心頻率,將uk(t)的頻譜變換到基帶上;3)對解調信號進行 H1高斯平滑,估計帶寬。
假設信號經VMD處理后分解為K個IMF,則變分約束模型為
(2)
式中:δ(t)為Dirac分布;*表示卷積;k=1,2,…,K;f為原始信號。
為求取變分約束模型的最優解,引入二次罰函數項α和Lagrange乘子λ可得
L({uk},{ωk},λ)=
(3)
VMD采用乘法算子交替的方法求取上述變分約束模型,得到最優解將信號分解成為K個窄帶IMF,其實現流程如下:
2)令n=n+1,執行整個循環。
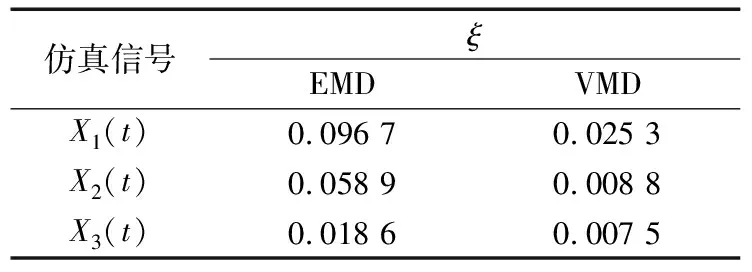
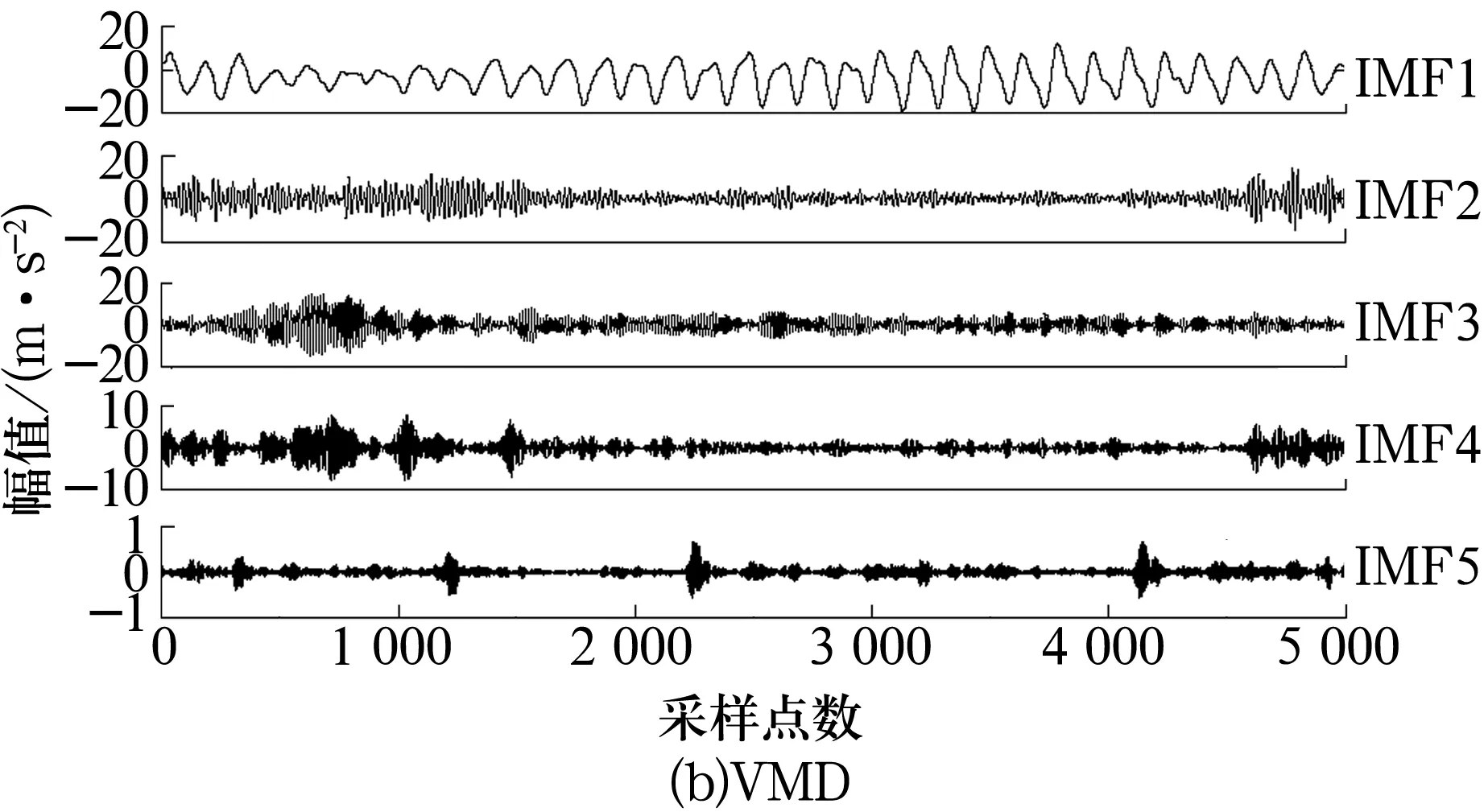
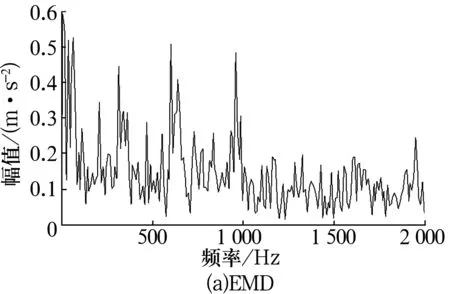
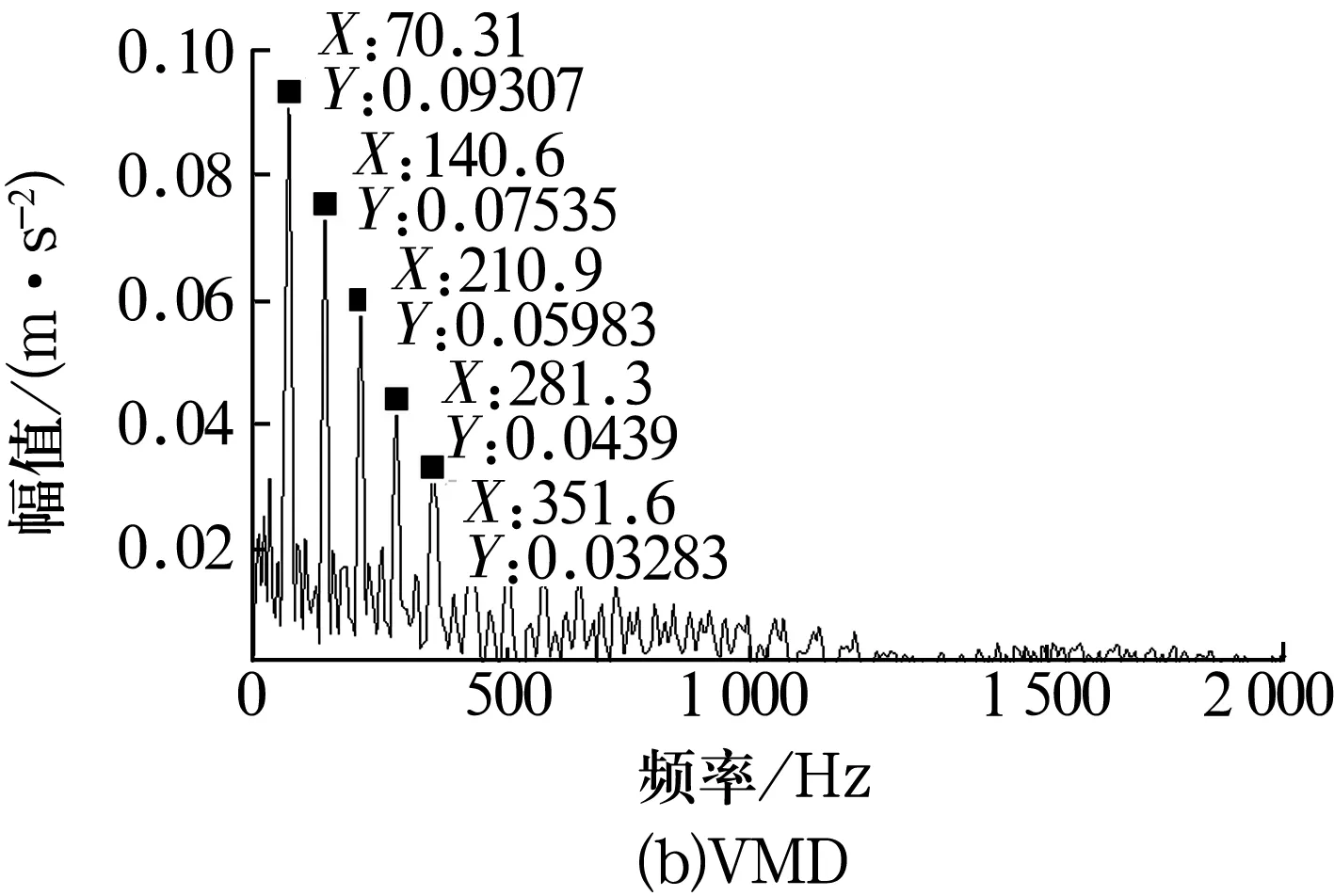
3)令k=0,k=k+1,當k 4)令k=0,k=k+1,當k 。(5) 5)更新λ為 (6) 使用MATLAB2011進行仿真分析,為算法比對的合理性,降低端點效應的影響,在EMD和VMD處理過程中均采用了鏡像延拓。VMD算法中的α取默認值2 000;K的取值采用觀察中心頻率的方法確定[11]。 仿真信號采用多頻信號X1(t)和標準差為1的隨機噪聲信號疊加所得,表達式為 X1(t)=[1+cos(2π×30t)]×cos(2π×125t)+[1+cos(2π×30t)]×cos[2π×155t+cos(2π×5t)]+[1+cos(2π×30t)]×cos(2π×185t)。(7) 采樣處理后的仿真信號如圖1所示,分別采用EMD(分解過程中采用基于互信息的方法去除了偽分量)和VMD算法進行處理,分解結果如圖2所示,分解后IMF的頻譜分析結果如圖3所示。 圖1 仿真信號 圖2 不同算法分解后的信號 圖3 分解后信號的頻譜圖 從圖3a中可以看出,IMF1中主要包含了155和185 Hz的頻率成分;IMF2中主要有125和155 Hz的頻率成分;IMF3則混合了65~95 Hz的頻率成分。結果表明,對于多分量加噪合成仿真信號,EMD算法的分解效果并不理想,模態混疊嚴重。這是由于一些微弱的信號和噪聲淹沒在待分解信號中, EMD在篩分過程中的3次樣條包絡擬合導致了分解偏差。微弱信號嵌入到強信號的絕大多數地方,EMD均能篩選并提取出,但當微弱信號僅出現在強信號的最大斜率范圍上時,微弱信號會以波內頻率調制的形式出現,并不產生額外的局部極值點,EMD很難提取,進而產生嚴重的模態混疊和偽分量。 從圖2b和圖3b可以看出, VMD不僅能有效去除偽分量,而且每個IMF均表現出某一尺度范圍的模態,彼此之間沒有模態混疊現象,實現了對仿真信號的多尺度表征,分解效果好于EMD,且具有很好的噪聲魯棒性。 EMD和VMD算法的分解結果都是正交的,即分解后各IMF的能量之和等于分解前信號的能量。但EMD和VMD的分解結果都不同程度地存在端點效應,影響信號的分解精度,導致虛假分量的產生,致使分解后IMF的總能量發生變化。在此,通過分析信號分解前后能量值的變化對比端點效應對EMD和VMD的影響[13]。 求取給定信號X(t)經過EMD和VMD分解后產生的IMF分量的能量 (8) 式中:E為給定信號X(t)或分解后各IMF的能量;x(i)為信號序列;n為信號的采樣點數。 比較各IMF能量總和與給定信號能量值之間的偏差,得到評價指標為 (9) 式中:Ex為給定信號的能量;Ep為第p個IMF的能量;K為IMF總數,包括分解的殘余項。 由定義可知,ξ越大,分解后的能量泄漏就越大,端點效應越強。ξ=0表示端點效應對分解結果幾乎沒有影響。構造仿真信號為 X2(t)=sin(2π×3t)+0.3sin(2π×11t)+ 0.8sin(2π×25t)+sin(2π×40t)+0.6cos(2π×100t), (10) X3(t)=[1+0.5cos(2π×4t)]×cos[2π×100t +2cos(2π×5t)]+[1+sin(2π×5t)]×sin[2π× 50t+0.5cos(2π×5t)]。 (11) 分別對3個仿真信號進行分析,采用EMD和VMD處理時不進行鏡像延拓,且分解時不去除偽分量,分解后求取的ξ見表1。由表可知,VMD的能量泄漏小,端點效應不明顯,結果優于EMD算法。 表1 能量泄漏評價指標 依據實測軸承振動信號,進一步對比分析EMD與VMD算法的分解結果。采用某變速箱軸承內圈故障振動信號,故障軸承型號為KOYO 1205,鋼球數Z=12,鋼球直徑Dw=7.12 mm,接觸角α=0,球組節圓直徑Dpw=38.5 mm,變速箱運行時軸的轉速約為600 r/min(fr=10 Hz),計算得內圈故障特征頻率為71.1 Hz。 利用電火花在軸承內圈溝道設置面積約3.58 mm2的點蝕,變速箱裝置簡圖如圖4所示,通過B&K3560數據采集儀采樣,傳感器布置如圖5所示,數據長度為65 536,選用變速箱軸承座的垂直振動信號(圖5中垂直振動傳感器采集的信號)作為故障診斷的研究對象。 圖4 變速箱裝置簡圖 圖5 傳感器布置圖 實測振動信號的時域波形如圖6所示,從圖中可以看出,正常信號波形與內圈故障信號波形類似,很難直接分辨軸承是否存在故障。 圖6 實測信號時域波形 截取信號前5 000個采樣點的數據作為研究對象。為增強故障脈沖信號,減小噪聲干擾,采用基于譜峭度和EMD/VMD的方法進行故障信號的預處理并進行故障診斷的分析對比。 在實測振動信號中,往往包含著故障信號及強烈的加性噪聲。由譜峭度的定義[14]可知,在信噪比很高的頻率處,譜峭度值大;而在噪聲強烈的頻率處,譜峭度值趨于0。因此,可以通過譜峭度對IMF進行篩選,尋找出包含故障信號的頻帶。計算故障信號經EMD或VMD算法分解后各IMF的譜峭度Ki(f),對Ki(f)進行歸一化處理,令 (12) 式中:λi為歸一化信息值,0≤λi≤1。利用信噪比高譜峭度值大的特點,將λi作為評判故障信號頻帶存在的指標,并設置故障頻帶分量的判斷閾值為δ,如果λi>δ,則認為該IMF為故障頻帶分量,否則予以剔除。基于譜峭度和EMD/VMD故障診斷算法流程如圖7所示。 圖7 基于譜峭度和EMD/VMD的包絡譜故障診斷流程圖 分別使用EMD和VMD算法對軸承內圈故障信號進行分解,結果如圖8所示。從圖中可以看出,分解結果非常復雜,很難分辨出具體的故障特征,分別計算各IMF的譜峭度值并歸一化處理,結果見表2。 設定閾值δ為0.8,選取EMD算法分解后的IMF2,IMF3和VMD算法分解后的IMF4,IMF5分別進行故障信號重構,并對重構后信號進行包絡譜分析,結果如圖9所示。 從圖9a可以看出,EMD算法分解重構后信號的解調效果欠佳,雖能觀察到70 Hz及部分倍頻,但軸承內圈故障信號的調制特征沒有解調出來,仍存在一定的模態混疊現象。 而從圖9b可以看出,經VMD算法分解重構后信號的包絡譜中有明顯的規律性沖擊成分,由于損傷點隨內圈轉動不斷變化,在70.3 Hz及倍頻 圖8 內圈故障信號的分解結果 表2 各IMF的譜峭度值歸一化結果 處(140.6,210.9,281.3 Hz等)有幅值逐漸下降的譜線,并且各倍頻處的兩邊有對稱的調制譜線。雖然與理論計算的內圈故障特征頻率(71.1 Hz)存在一定差值,但也要考慮鋼球在旋轉過程中并非是純滾動,而且軸承存在幾何誤差和裝配誤差等因素,因此,可認為VMD算法處理后信號的包絡譜圖呈現出了典型的軸承內圈故障特征,從而判定軸承存在內圈故障。同理,對軸承外圈及鋼球故障進行分析,也取得了很好的效果。 圖9 重構信號的包絡譜圖 VMD和EMD算法均可對信號進行不同尺度的表征,但VMD算法避免了模態混疊以及偽分量的產生,能較好地在不同尺度下表征原信號,且在噪聲魯棒性和避免端點效應方面均優于EMD算法。將VMD和EMD分別與譜峭度相結合,對實測軸承振動信號的故障診斷結果表明,VMD算法的包絡譜能更好地反映故障頻段的變化及軸承故障的包絡譜特征。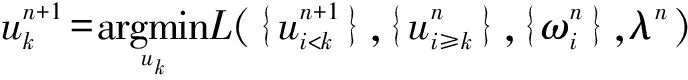
2 仿真分析
2.1 仿真信號的分解對比

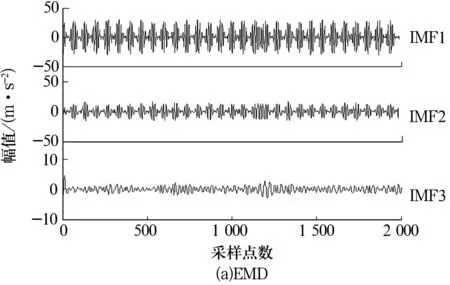
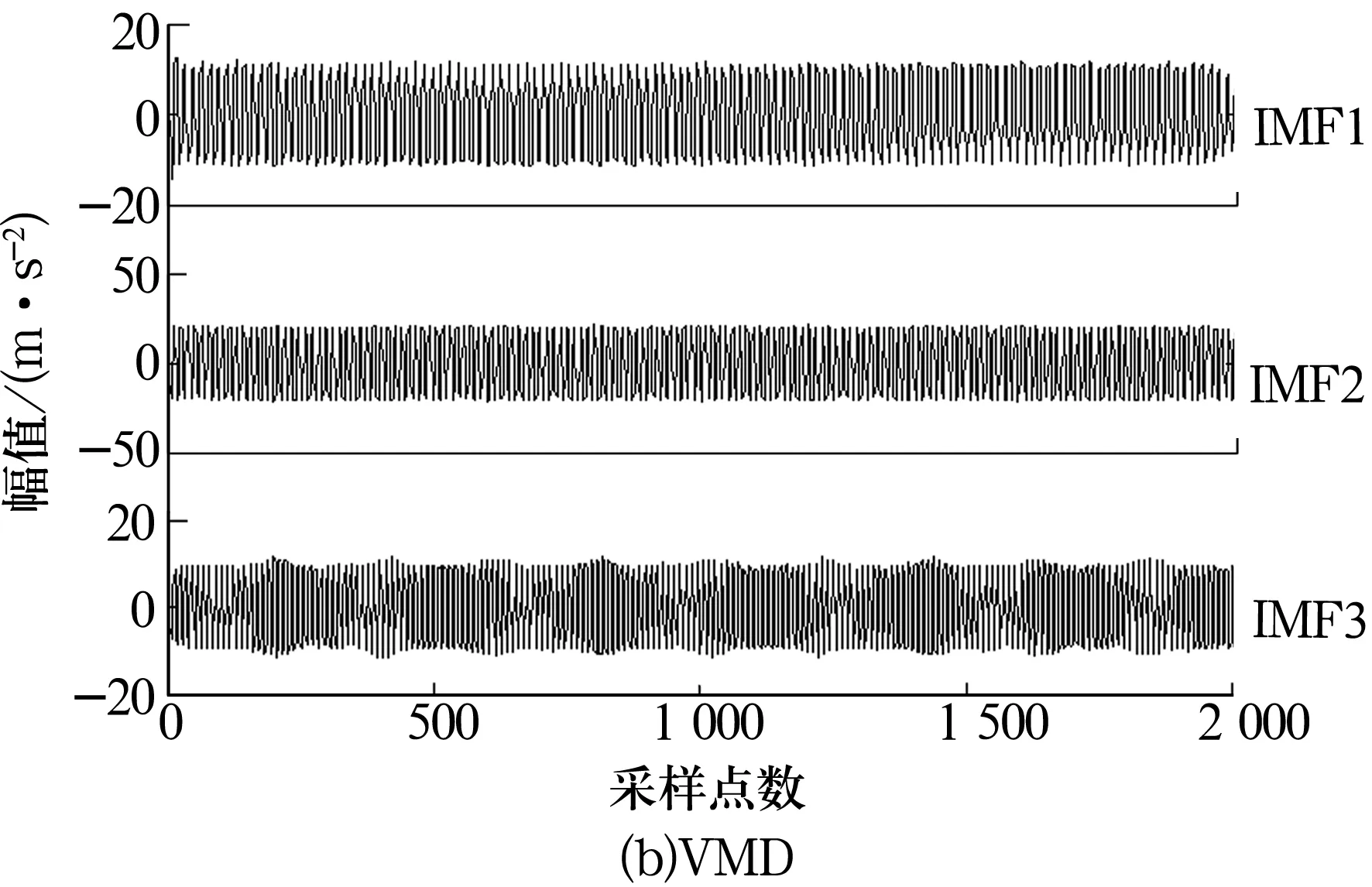

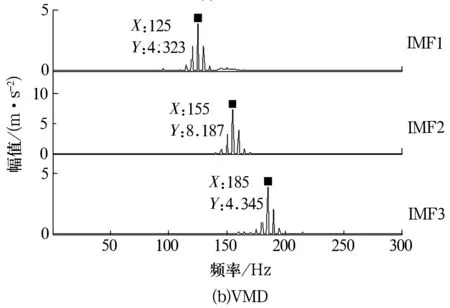
2.2 端點效應的影響
3 基于譜峭度和VMD算法的包絡譜故障診斷方法
3.1 試驗條件
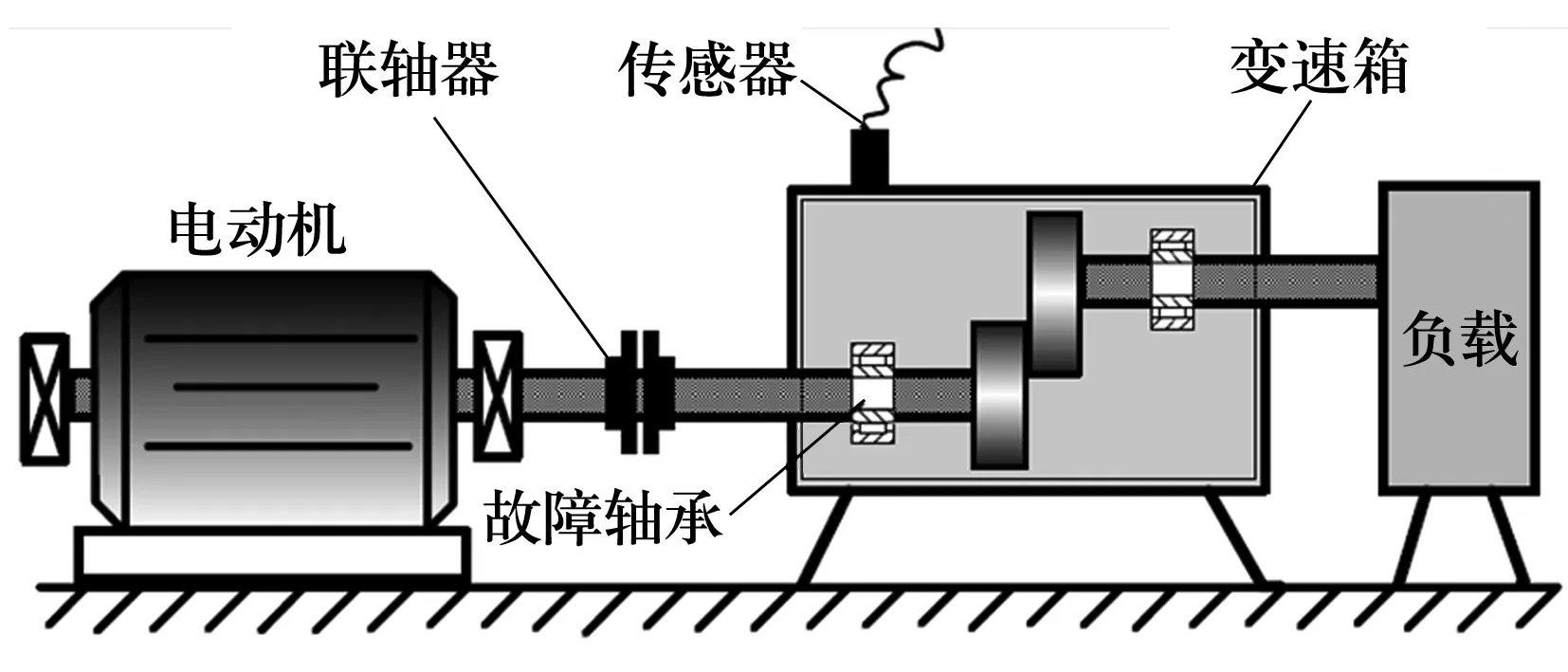

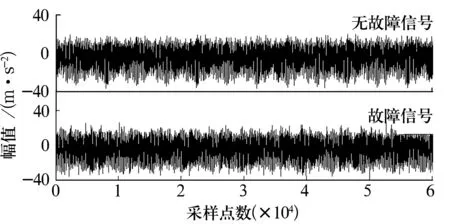
3.2 診斷流程
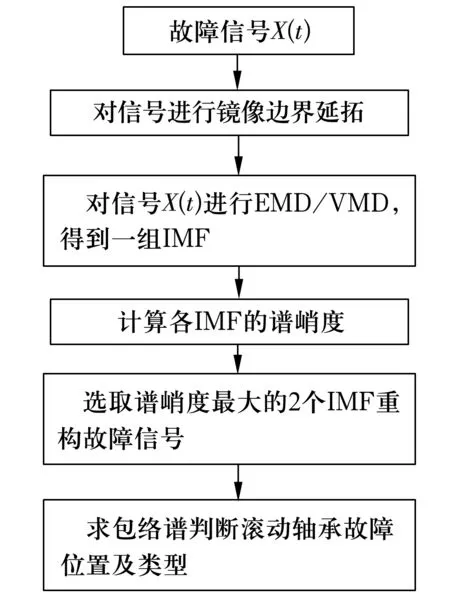
3.3 對比分析


4 結束語

