基于顯式動力學的推力滾針軸承振動分析與試驗研究

余光偉，王嘉鑫，陳曉陽，盧俊，黃迪山

(上海大學 機電工程與自動化學院，上海 200072)

推力滾針軸承因安裝所需軸向空間小等優點，廣泛應用于機械電子儀器、電動工具、汽車變速器等機械設備中[1]。隨著對機械動力性能和噪聲要求的提高，推力滾針軸承的振動性能顯得非常重要,故有必要進行專門分析。

基于軸承運轉時滾針與滾道接觸處產生的能量損失最小的假設，推導出推力滾針軸承各零件速度的計算方法。以AXK2542推力滾針軸承為例，在ANSYS/LS-DYNA中建立模型，并采用顯式動力學有限元法對其進行仿真分析，得到了軸承各零件的速度，與理論計算結果相比誤差較小。通過該有限元法分析了轉速、軸向載荷對推力滾針軸承振動加速度的影響，并進行了試驗驗證。說明采用ANSYS/LS-DYNA軟件建立的有限元模型可用于對推力滾針軸承的振動分析。

1 顯式動力學

ANSYS/LS-DYNA是一個以顯式動力學為主，隱式動力學為輔的有限元求解器。顯式動力學采用中心差分方法，既不需要求解切線剛度，也不需要進行平衡迭代，可節省大量計算資源和時間。系統的求解方程為

(1)

中心差分法解的穩定條件為

(2)

式中：Δter為臨界時間間隔；Tn為有限元系統的最小固有振動周期。

2 軸承各零件速度計算模型

滾針與墊圈速度示意圖如圖1所示，假設軸承座圈固定，軸圈以角速度ωh旋轉，保持架和滾針公轉角速度為ωc，滾針自轉角速度為ωr。r為滾針半徑，re和ri分別為滾針兩端面到軸承軸線的距離。

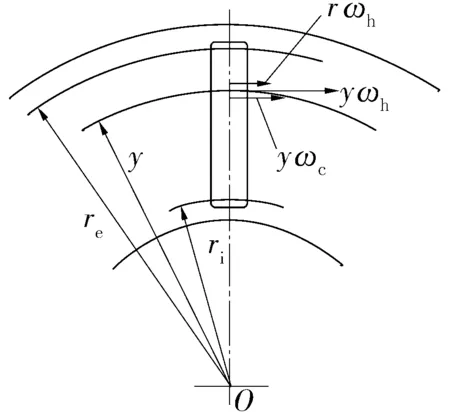
(a) 滾針與軸圈

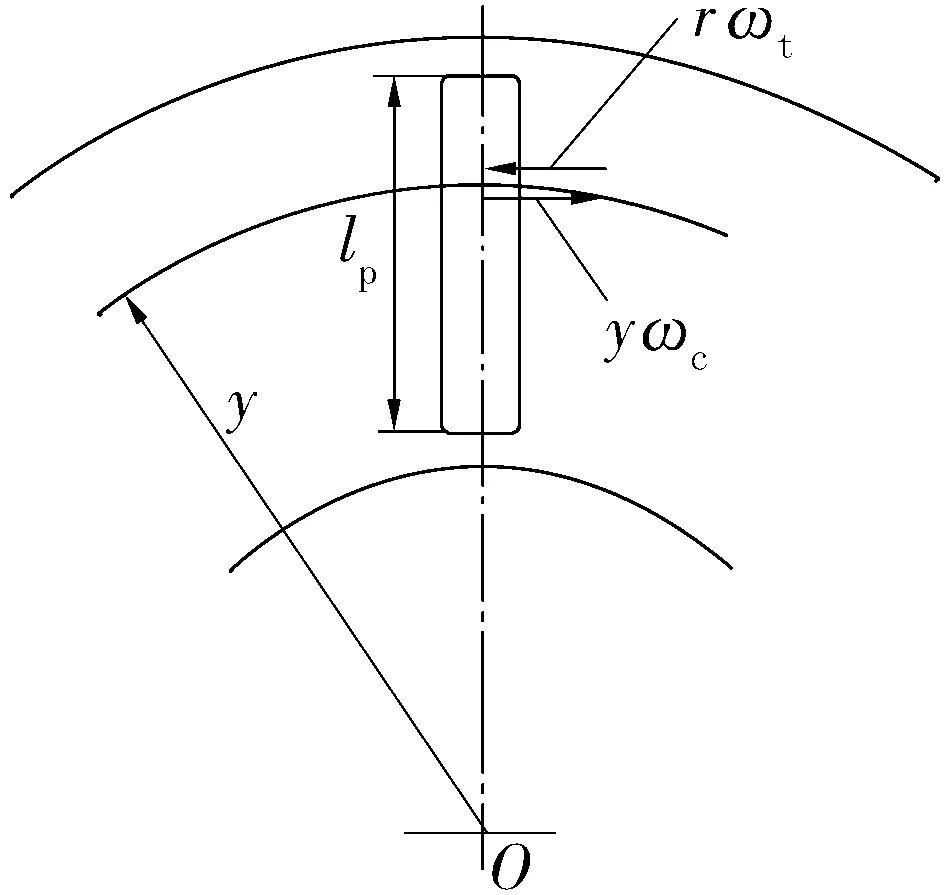
(b) 滾針與座圈

由圖1可知，在半徑y處滾針與軸圈接觸面的相對滑動速度為

Sr1=yωh-(yωc+rωr)，

(3)

由于滾針與軸圈和座圈之間的相對滑動造成的能量損失[2]為

(4)

式中：Z為滾針數；μ為滾針與軸圈和座圈之間的動摩擦因數；pm為平均接觸應力；b為接觸橢圓半寬。

根據Hertz理論得[3]

Q1=Fa/Z,

(5)

式中：Q1為單個滾針上的載荷；Fa為軸向載荷；lp為滾針有效長度。

由(4)式、(5)式得

(6)

同理可得，滾針與座圈接觸面之間的相對滑動速度為

Sr2=yωc-rωr，

(7)

能量損失為

(8)

則總能量損失為

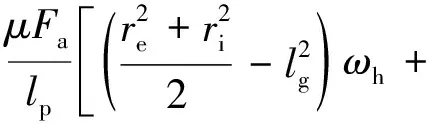
(9)

式中：lg為滾針和墊圈之間無相對滑動處到軸承軸線的距離。

滾針的自轉角速度和公轉角速度ωr取決于能量損失Et，當能量損失最小時

(10)

由(10)式可得

(11)

由此可見，無相對滑動的位置位于滾針中點。將(11)式代入(3)式和(7)式得

(12)

(13)

3 有限元模型

3.1 建立模型

以AXK2542推力滾針軸承為例，其主要結構參數見表1。

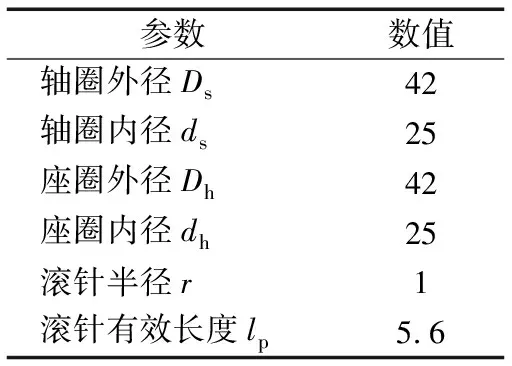
表1 主要結構參數

采用自下而上的方式建立推力滾針軸承的幾何模型,并對模型做如下簡化：1)忽略軸承的倒角和邊棱對內部應力的影響；2)不考慮墊圈波紋度和表面粗糙度的影響；3)不考慮潤滑油膜的影響。將幾何模型通過標準圖形輸入接口導入到ANSYS/LS-DYNA前處理器中，有限元單元選用Solid164，采用掃略分網、映射分網和自由分網相結合的方式劃分網格。軸圈、座圈上表面設置為Shell163單元，以便施加轉速和載荷。

軸圈、座圈和滾針采用六面體單元，保持架采用四面體單元。建立的有限元模型如圖2所示。

圖2 推力滾針軸承有限元模型

3.2 材料參數

由于軸承塑性變形很小，因此將軸圈、座圈和滾針均設為線彈性材料。在仿真模型中，假設軸圈、座圈和滾針材料[4]均為GCr15鋼，保持架材料為3Cr13鋼，其材料力學參數見表2。

表2 材料力學參數

3.3 載荷與約束

參照試驗，壓力簡化為均布壓力，同轉速一起施加在軸圈上表面，座圈設為全約束。

3.4 接觸與邊界條件

推力滾針軸承運轉過程中，滾針與軸圈、座圈之間的接觸設為自動面-面接觸，靜摩擦因數均為0.35[5]，動摩擦因數均為0.16；保持架與滾針、 軸圈和座圈之間的接觸設為自動面-面接觸，靜摩擦因數均為0.002，動摩擦因數均為0.001；座圈與底座之間的接觸設為自動面-面接觸，靜摩擦因數均為0.35，動摩擦因數均為0.16。試驗測量推力滾針軸承振動時，軸圈連接在剛性很大的軸上，座圈固定在軸承座上，由于Solid164單元沒有旋轉自由度，因此將軸圈上表面和座圈下表面設置為剛性面，模擬軸承的邊界條件。

4 試驗驗證

推力滾針軸承測振儀如圖3所示，被測軸承置于底座上，通過氣壓裝置使其與主軸壓緊，主軸帶動軸圈轉動，壓電加速度傳感器的傳振桿與座圈底面接觸測量振動，將被測軸承的振動加速度信號轉換成電信號，經信號調理模塊放大、濾波后，傳至數據采集卡，再由工控機進行分析處理。通過調節主軸電動機轉速來改變軸承轉速，通過雙螺母調節彈簧壓縮量來改變軸向載荷。

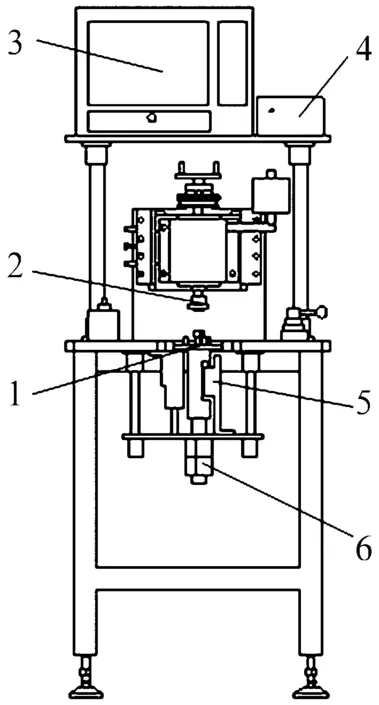
1—底座；2—主軸；3—工控機；4—信號調理模塊；5—傳感器；6—雙螺母

5 結果分析

5.1 速度分析

對軸圈施加400 N的軸向載荷，轉速為1 800 r/min，為方便與理論值對比，取軸圈外側面節點49 726、保持架外側面節點43 540和滾針外端面邊沿節點300(圖4)，各節點的速度曲線如圖5所示。

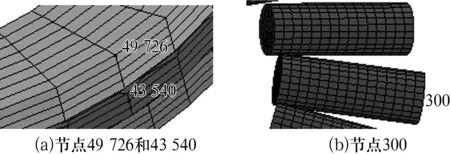
圖4 節點49 726，43 540和300的位置

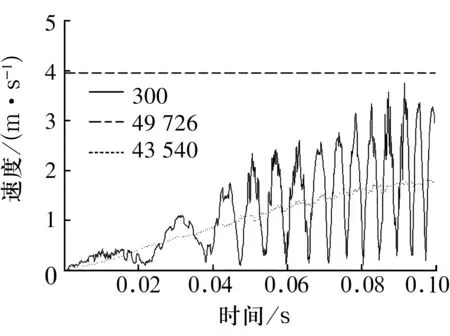
圖5 各節點速度

由圖5可知，軸圈速度保持恒定，保持架轉速隨時間增長而增大，經過約0.08 s后穩定，滾針外端面邊沿的線速度呈周期性變化。

軸承各零件速度計算值與仿真值對比見表3，由表可知，仿真值與理論計算值相差不大。

表3 軸承零件速度計算值與仿真值對比

5.2 振動加速度分析

選取座圈底面邊沿的節點40 916(圖6)，當施加在軸圈上的軸向載荷為400 N、轉速為1 800 r/min時，節點加速度曲線如圖7所示。

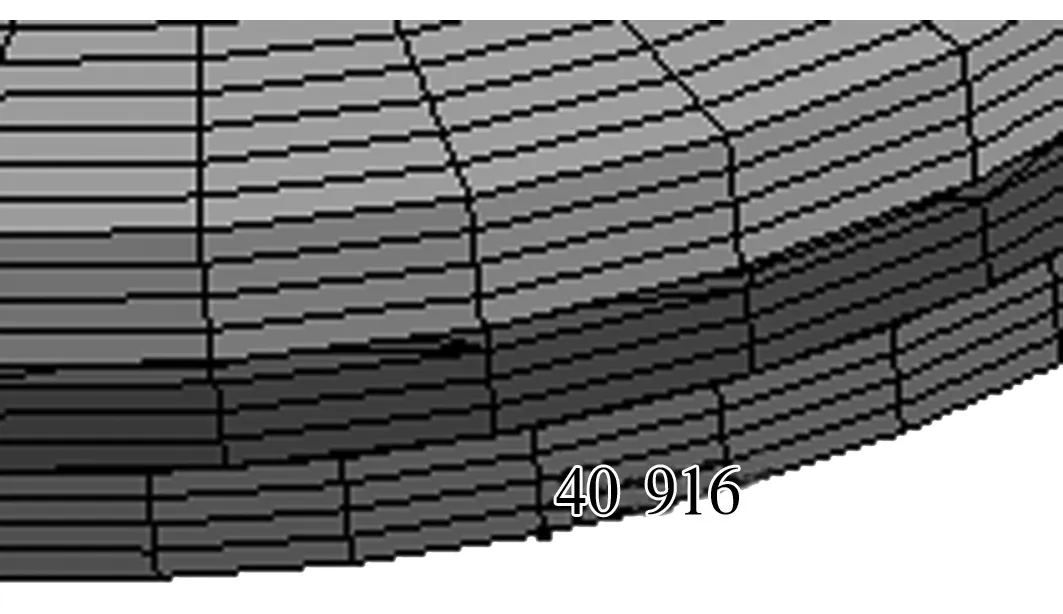
圖6 節點40 916的位置

圖7 節點40 916的加速度

軸承振動加速度值[6]為

(14)

式中：a為振動加速度均方根值；g為重力加速度。

5.2.1 轉速對振動加速度的影響

軸向載荷為400 N時，軸承振動加速度隨轉速的變化如圖8所示。由圖8可知，隨轉速增大，振動加速度的仿真值和測量值均無明顯變化，仿真值比測量值小約4 dB。其原因為：1)仿真時忽略了墊圈波紋度和材料表面粗糙度等工藝參數的影響;2)試驗測試系統中不可避免地存在噪聲干擾。

圖8 振動加速度隨轉速的變化

5.2.2 軸向載荷對振動加速度的影響

轉速為1 800 r/min時，軸承振動加速度隨軸向載荷的變化如圖9所示。由圖9可知，隨軸向載荷增大，軸承振動加速度也增大，仿真值的增幅明顯大于測量值，這是由于仿真時忽略了潤滑油膜的影響，在實際工況中，滾針與滾道之間會形成潤滑油膜，可以起到減振隔振的作用，緩解了軸向載荷對振動加速度的影響。

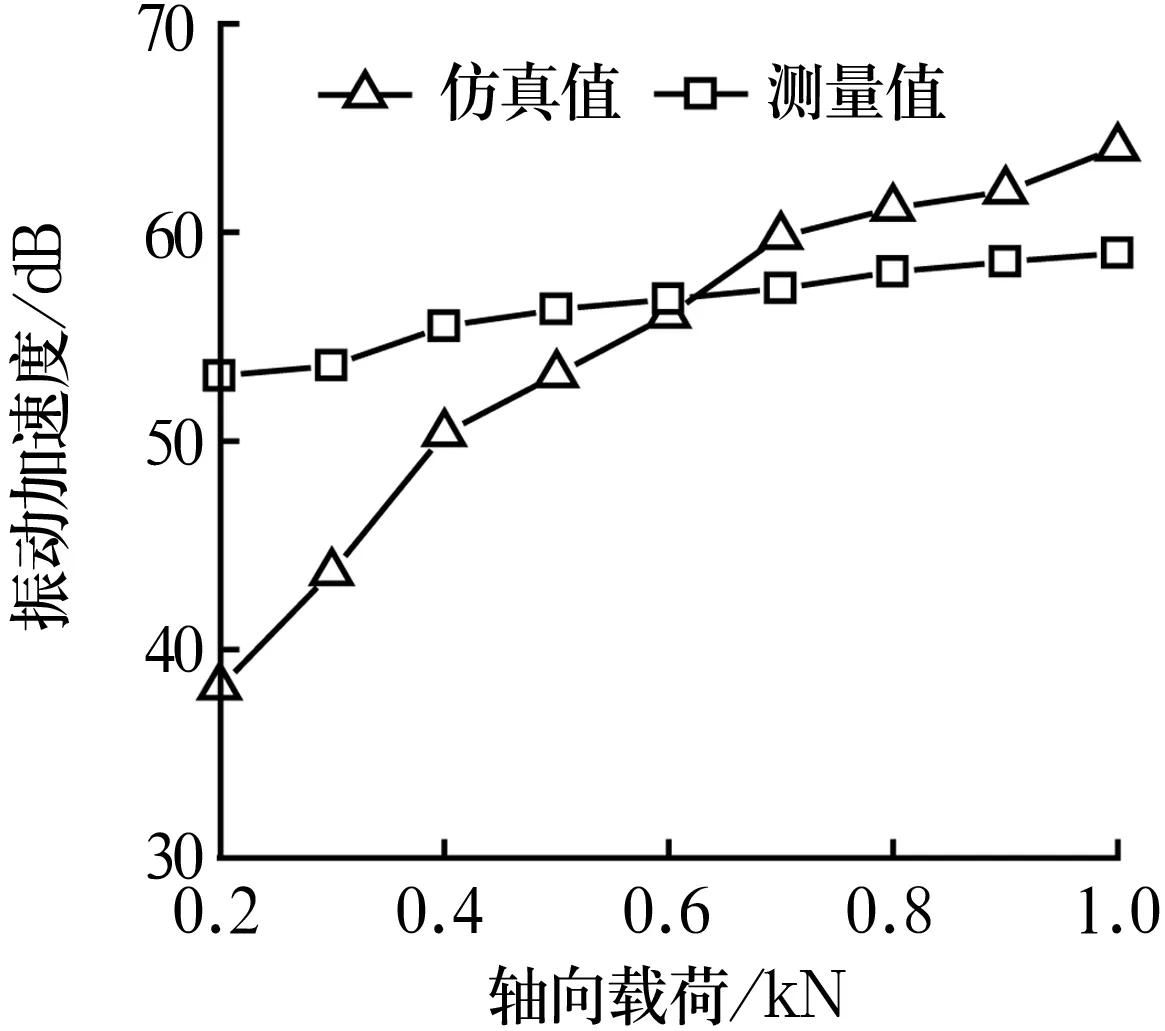
圖9 振動加速度隨軸向載荷的變化

5.2.3 滾針個數對振動加速度影響

軸向載荷400 N、轉速1 800 r/min時，軸承振動加速度隨滾針個數的變化如圖10所示。由圖10可知，當滾針個數小于35時，軸承振動加速度隨著滾針個數的增加而減小，這是由于滾針個數增多使得單個滾針所受軸向載荷減小；但當滾針個數為40時，其振動加速度值有所上升，這是因為隨著滾針個數的增多，滾針與保持架間的耦合作用增強，滾針與保持架接觸頻繁[7]，導致軸承的振動增大。

圖10 振動加速度隨滾針個數的變化

5.2.4 滾針直徑對振動加速度的影響

軸向載荷400 N、轉速1 800 r/min時，軸承振動加速度隨滾針直徑的變化如圖11所示。由圖11可知，隨著滾針直徑的增大，軸承的振動加速度也增大。

圖11 振動加速度隨滾針直徑的變化

6 結論

1)在所研究的速度范圍內，轉速對推力滾針軸承的振動加速度影響很小。

2)隨軸向載荷的增大，推力滾針軸承的振動加速度也增大。

3)存在一個最佳的滾針個數，使得推力滾針軸承的振動加速度最小。

4)隨滾針直徑的增大，推力滾針軸承的振動加速度也增大。