立體幾何中策略創造的培養

羅莎

【摘要】數學的學習是一個再創造的過程，教師提供學生數學學習中再創造的平臺.學生的策略創造培養，是一個長期的過程，對于策略創造的培養，可能是一種思想方法的遷移應用，也可能是一個基本知識點的發散訓練.本文就立體幾何中空間直角坐標系的方法的應用，可將學生無法入手的問題，變成有法可解，有規律可循；

【關鍵詞】策略創造；空間直角坐標系

數學的學習是一個再創造的過程，教師提供學生數學學習中再創造的平臺.張奠宙教授認為：“數學教學的任務之一，是將邏輯演繹編寫的教材還原成生動活潑的思維創造活動”[1].同時張奠宙教授認為：“數學思維是策略創造和邏輯演繹的結合，而且策略創造處于主導方面，邏輯演繹是基礎方面”[1].對于學生創新思維的培養，離不開學生的策略創造.學生的策略創造培養，是一個長期的過程，逐步生成，它有可能是“觀察實驗，引發猜想；數形結合，萌生構想；類比模擬，積極聯想；發散求異，多方設想；思維設計，允許幻想；直覺頓悟，突發奇想；群體智力，民主暢想”[2].在教學過程中，實現培養學生的策略創造，教師就要提供再創造的階梯，以一步一步的培養和激勵學生策略創造的活動.

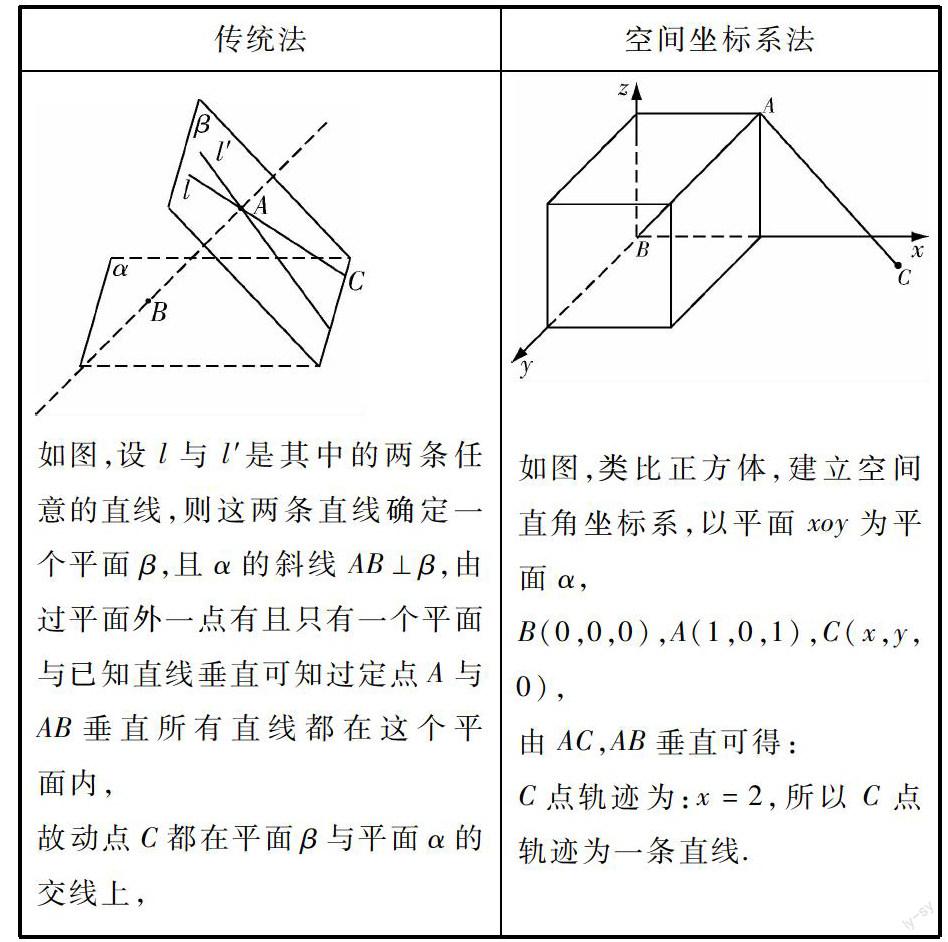
教師提供再創造的一個環節，可以是一種思想方法的針對性滲透.比如，立體幾何中的傳統法需要很強的空間感，解決有的問題時學生感到吃力.向量方法或空間坐標系法在課本中，主要解決線線，線……