函數(shù)的導(dǎo)數(shù)易錯(cuò)題分析研究*

景慧麗（火箭軍工程大學(xué)理學(xué)院，陜西西安710025）

?

函數(shù)的導(dǎo)數(shù)易錯(cuò)題分析研究*

景慧麗
（火箭軍工程大學(xué)理學(xué)院，陜西西安710025）

摘要：函數(shù)導(dǎo)數(shù)的計(jì)算是微積分學(xué)中的一個(gè)重點(diǎn)，大部分學(xué)員在求函數(shù)的導(dǎo)數(shù)時(shí)經(jīng)常出錯(cuò)。本文分析了學(xué)員在求導(dǎo)數(shù)過程中經(jīng)常出現(xiàn)的錯(cuò)誤，歸納了錯(cuò)誤類型，并且就每種錯(cuò)誤類型給出了相應(yīng)的例題、錯(cuò)誤解法，重點(diǎn)分析了錯(cuò)解原因，最后給出了正確解法和注意事項(xiàng)。

關(guān)鍵詞：導(dǎo)數(shù)；易錯(cuò)題；分析

Abstract:Calculating the functional derivative is one of the most important concepts of the calculus. But most of the students often make mistakes when calculating the functional derivative. The error that students have in the process of problem solving is concluded in this paper. Furthermore，corresponding examples of each type of error are given，and the wrong solution is analyzed，and the correct solution and some matters needing attention are discussed.

Keywords:derivative；easy wrong topic；analysis.

導(dǎo)數(shù)是微積分學(xué)中最基本的概念也是最重要的概念之一，相應(yīng)地，求函數(shù)的導(dǎo)數(shù)也是微積分學(xué)中的重點(diǎn)和難點(diǎn)。求函數(shù)的導(dǎo)數(shù)常用的方法有：利用導(dǎo)數(shù)的定義、利用四則運(yùn)算求導(dǎo)法則、利用復(fù)合函數(shù)求導(dǎo)法則等等，每種方法都有自己的使用條件和適用范圍。但是，作者在教學(xué)中發(fā)現(xiàn)，大部分學(xué)員尤其是初學(xué)者，遇到求導(dǎo)數(shù)的題目，不管是否滿足條件就直接利用運(yùn)算法則來計(jì)算，有時(shí)結(jié)果盡管“碰巧”正確，但求解方法卻是錯(cuò)誤的。為了幫助學(xué)員掌握函數(shù)導(dǎo)數(shù)的求法，并能熟練、正確地求函數(shù)的導(dǎo)數(shù)，作者結(jié)合教學(xué)實(shí)踐就學(xué)員在解題過程中經(jīng)常出現(xiàn)的錯(cuò)誤進(jìn)行了分析，歸納了學(xué)員解題過程中所出現(xiàn)的錯(cuò)誤類型，分析了出錯(cuò)的原因，并給出了正確解法。常見的錯(cuò)誤主要有以下幾種。

一、在應(yīng)用導(dǎo)數(shù)的定義式時(shí)常犯的錯(cuò)誤

例1.設(shè)f'（x0）存在，求極限

［錯(cuò)解分析］上述解法錯(cuò)在

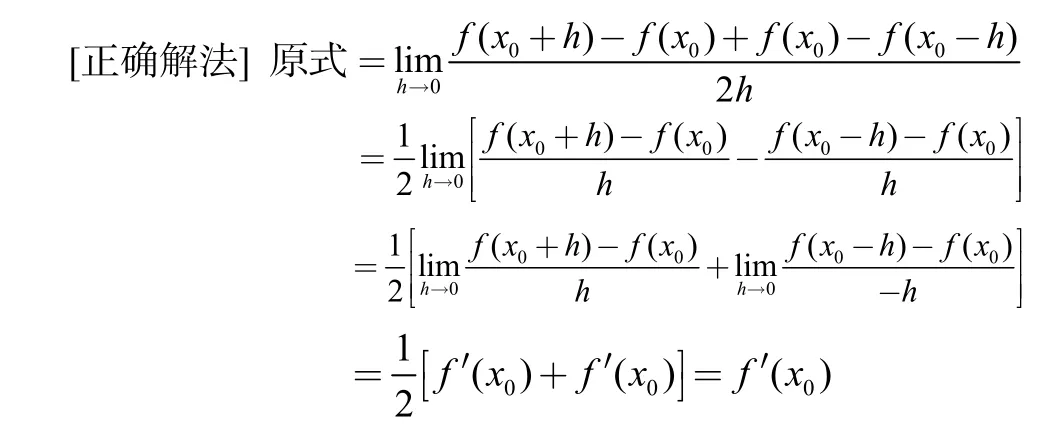
注1上述解法出錯(cuò)的根本原因是不理解導(dǎo)數(shù)定義式的實(shí)質(zhì)。函數(shù)f（x）在點(diǎn)x0處的導(dǎo)數(shù)f'（x0）的定義式中必有f（x0）這一項(xiàng)，如果沒有這一項(xiàng)，絕對不是f'（x0）的定義。另外，從定義式中可以看出f（x）在點(diǎn)x0處的導(dǎo)數(shù)f'（x0）是否存在以及f'（x0）的值的大小都與f（x）在點(diǎn)x0處的函數(shù)值f（x0）有關(guān)［1］。

注2由f'（x0）存在可以得到極限存在，但是，絕對不能由極限存在，得到f'（x0）存在，此時(shí)f'（x0）也可能不存在，例如函數(shù)f（x）=|x|在x=0處就屬于這種情況，具體解題過程不再贅述。

二、求函數(shù)在一點(diǎn)的導(dǎo)數(shù)時(shí)常犯的錯(cuò)誤

求函數(shù)在一點(diǎn)處的導(dǎo)數(shù)通常有兩種方法：方法一是直接利用導(dǎo)數(shù)的定義來求，方法二是先求出導(dǎo)函數(shù)再代值。但是，大部分同學(xué)經(jīng)常是看到這類題目會(huì)不假思索地應(yīng)用方法二，導(dǎo)致錯(cuò)誤。

例2［2］.設(shè)f（x）=（x-a）φ（x），其中φ（x）在x=a處連續(xù)，求f'（a）。

［錯(cuò)解］因?yàn)閒'（x）=φ（x）+（x-a）φ'（x），所以f'（a）=φ（a）+（a-a）φ' （a）。

［錯(cuò)解分析］上述結(jié)果正確，但是解題方法是錯(cuò)誤的，即步驟“f'（x）=φ（x）+（x-a）φ'（x）”是錯(cuò)誤的。因?yàn)轭}目只說φ（x）在點(diǎn)x=a處連續(xù)，沒說其可導(dǎo)，所以φ'（x）是否存在是不知道的，當(dāng)然由于φ（x）是抽象函數(shù)，其可導(dǎo)性也是不能判斷的，因此f'（x）也不一定存在，所以上述解法是錯(cuò)誤的。

［正確解法］本題只能用導(dǎo)數(shù)的定義來求，即

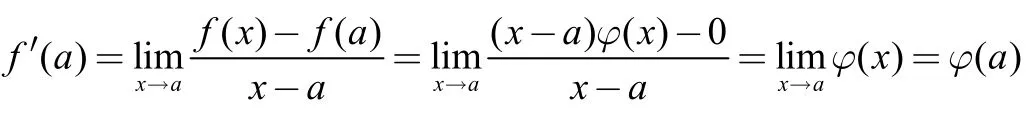
注3求抽象函數(shù)在連續(xù)點(diǎn)處的導(dǎo)數(shù)必須用導(dǎo)數(shù)的定義求。

注4利用導(dǎo)數(shù)的定義求函數(shù)在一點(diǎn)的導(dǎo)數(shù)是一種常用的方法，即便是初等函數(shù)，有時(shí)候?yàn)榱饲蠼夥奖悖残枰枚x來求導(dǎo)。例如，設(shè)f（x）=x（x+1）（x+2）…（x+2015），顯然利用乘積求導(dǎo)法則求f'（0）是比較麻煩的，但是利用導(dǎo)數(shù)的定義求f'（0）是非常簡便的，這里具體解題步驟不再贅述。

三、求分段函數(shù)在分段點(diǎn)處的導(dǎo)數(shù)時(shí)常犯的錯(cuò)誤

求分段函數(shù)在分段點(diǎn)處的導(dǎo)數(shù)是一個(gè)難點(diǎn)也是重點(diǎn)。一般地，求分段函數(shù)在分段點(diǎn)處的導(dǎo)數(shù)都需要應(yīng)用導(dǎo)數(shù)的定義來求，但是在教學(xué)中筆者發(fā)現(xiàn)，大部分學(xué)員還是掌握不了這類題目的求解方法，遇到這類題目就“隨心所欲”，想怎么做就怎么做，經(jīng)常出錯(cuò)。

例3［1］.設(shè)。

且f'（x）在x=0處無定義，所以f'（0）不存在。

［錯(cuò)解分析］上述解法錯(cuò)在錯(cuò)用了先求導(dǎo)函數(shù)再代值這個(gè)方法來求函數(shù)在一點(diǎn)的導(dǎo)數(shù)值。當(dāng)函數(shù)f（x）在點(diǎn)x0處可導(dǎo)，即f'（x0）存在，并且導(dǎo)函數(shù)f'（x）在點(diǎn)x0處有定義時(shí)，要求f'（x0），可以先求出導(dǎo)函數(shù)f'（x），再把點(diǎn)x0代入。但是絕對不能由f'（x）在點(diǎn)x0處沒有定義，得出f'（x0）不存在的結(jié)論，f'（x0）也有可能存在，此時(shí)必須用導(dǎo)數(shù)的定義來判斷。因此本解法是錯(cuò)誤的。［正確解法］本題只能用導(dǎo)數(shù)的定義來求，即

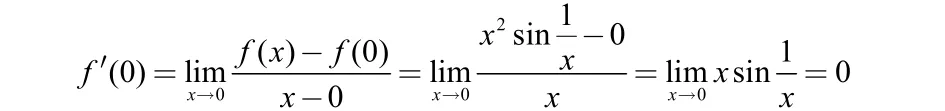
注5分段函數(shù)在分段點(diǎn)處的導(dǎo)數(shù)一般需要用定義來求，如果在分段點(diǎn)的左右兩側(cè)函數(shù)的表達(dá)式不一樣，還需要求左、右導(dǎo)數(shù)，如例3如果改為，則需要分別求出左導(dǎo)數(shù)f'（0）和右導(dǎo)數(shù)（0），再判斷f'（0）是否存在。

注6例3只是學(xué)員在求分段函數(shù)在分段點(diǎn)處的導(dǎo)數(shù)時(shí)出現(xiàn)的錯(cuò)誤之一，其實(shí)學(xué)員在解這類題目時(shí)還經(jīng)常犯例4中所出現(xiàn)的3類錯(cuò)誤。

例4［3］.設(shè)，求f′（1）。

當(dāng)x>1時(shí)，f'（x）=（x2）'=2x，所以f'（1）=2，

綜上，f'（1）=2。

所以，f'（1）=2。

［錯(cuò)解分析］錯(cuò)解1錯(cuò)誤的原因是這種解法是沒有理論依據(jù)的，是毫無意義的，該解法是學(xué)員“隨心所欲”地“創(chuàng)造”出來的，但是這種錯(cuò)誤解法也是學(xué)員經(jīng)常所出現(xiàn)的。

所以，f'（1）不存在。

注7分段函數(shù)在分段點(diǎn)處的導(dǎo)數(shù)最好用定義來求，盡管也可以利用導(dǎo)函數(shù)極限定理來求，但是需要判斷函數(shù)是否滿足定理的條件，這個(gè)過程有時(shí)也是比較麻煩的，所以不建議大家利用導(dǎo)函數(shù)極限定理來求段函數(shù)在分段點(diǎn)處的導(dǎo)數(shù)。

四、求參數(shù)方程所確定的函數(shù)的高階導(dǎo)數(shù)時(shí)常犯的錯(cuò)誤

例5［5］.設(shè)函數(shù)y=y（x）由所確定，求。

［錯(cuò)解分析］上述解法錯(cuò)在“（y'）'=（tant）'”這一步。因?yàn)楹瘮?shù)的自變量是x，而不是t，且二階導(dǎo)是一階導(dǎo)再對x求導(dǎo)，而不是對t求導(dǎo)，因此上述解法所以是錯(cuò)誤的。其實(shí)，上述解法中是等于（tant）'的。

［正確解法］

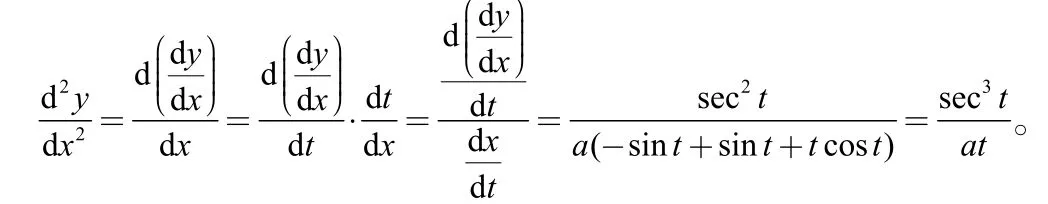
以上就是學(xué)員們在求函數(shù)的導(dǎo)數(shù)時(shí)經(jīng)常出現(xiàn)的錯(cuò)誤，其實(shí)只要學(xué)員真正理解了導(dǎo)數(shù)的概念，掌握了求導(dǎo)數(shù)的各種方法的本質(zhì)及使用范圍和技巧，上述錯(cuò)誤是完全可以避免的。當(dāng)然，教員也應(yīng)允許學(xué)員在學(xué)習(xí)過程中出錯(cuò)，學(xué)員對概念理解有偏差、解題過程出現(xiàn)錯(cuò)誤都是正常的，都是符合實(shí)際情況的。另外，教員也要正確看待這些“錯(cuò)題”資源，這些資源都是非常寶貴的教學(xué)資源，心理學(xué)家蓋耶曾說過：“誰不考慮嘗試錯(cuò)誤，不允許學(xué)生犯錯(cuò)誤，就將錯(cuò)過最富成效的學(xué)習(xí)時(shí)刻。”［6］所以，在教學(xué)中，教員要主動(dòng)挖掘?qū)W員“錯(cuò)題”中的“閃光點(diǎn)”，及時(shí)進(jìn)行探究、分析和講評，這不但可以為學(xué)員創(chuàng)造新的學(xué)習(xí)機(jī)會(huì)，而且還可以培養(yǎng)學(xué)員的問題意識［7］，培養(yǎng)和提高學(xué)員發(fā)現(xiàn)問題的能力。

參考文獻(xiàn)

［1］馬知恩，王綿森.高等數(shù)學(xué)疑難問題選講［M］.第一版.北京：高等教育出版社，2014：77-80.

［2］陳文燈，武海燕，李冬紅.高等數(shù)學(xué)復(fù)習(xí)指導(dǎo)-思路、方法與技巧［M］.第二版.北京：清華大學(xué)出版社，2011：103.

［3］同濟(jì)大學(xué)應(yīng)用數(shù)學(xué)系.高等數(shù)學(xué)（上）［M］.第七版.北京：高等教育出版社，2014：83.

［4］華東師范大學(xué)數(shù)學(xué)系.數(shù)學(xué)分析（上）［M］.第三版.北京：高等教育出版社，2002：122.

［5］高等學(xué)校工科數(shù)學(xué)課程教學(xué)指導(dǎo)委員會(huì)本科組.高等數(shù)學(xué)釋疑解難［M］.第一版.北京：高等教育出版社，1992：48.

［6］錢怡杰.基于錯(cuò)題的高三基礎(chǔ)會(huì)計(jì)教學(xué)探究［J］.經(jīng)營管理者，2015，2：372-373.

［7］景慧麗.第二類曲面積分易錯(cuò)題分析研究［J］.商丘職業(yè)技術(shù)學(xué)院學(xué)報(bào)，2015，5：4-8.

中圖分類號：O172

文獻(xiàn)標(biāo)志碼：A

文章編號：2096-000X（2016）10-0260-03

*基金項(xiàng)目：火箭軍工程大學(xué)2015年度教育教學(xué)立項(xiàng)課題（項(xiàng)目編號：EPGC2015008）

作者簡介：景慧麗（1983-），女，漢族，河南平頂山人，碩士，講師，研究方向：大學(xué)數(shù)學(xué)教育，最優(yōu)化理論與應(yīng)用。