讓思維在探究中放飛

張秒

蘇科版《義務教育課程標準實驗教科書·數學》在每一章節之后所設置的“復習題”共分為“復習鞏固”、“靈活應用”、“探索研究”三個層面，以供教師在本章復習教學時選用.在教學實踐中，我們發現：不少教師尤其是一些年輕的教師對“探索研究”層面的復習題往往沒有主動探究的意識，從不知道如何探究到無可奈何放棄探究，教師在課堂上怎么能引導學生進行探究性學習呢？本文將結合八年級上冊第一章復習題中的第15題談談自己的一些做法.

原題 （1）野營活動中，小明用一張等腰三角形的鐵皮代替鍋，烙一塊與鐵皮形狀、大小相同的餅.烙好一面后把餅翻身，這塊餅仍能正好落在“鍋”中.這是為什么？

（2）小麗用如圖①的一張直角三角形的鐵皮代替鍋，烙一塊與鐵皮形狀、大小相同的餅.如果烙好一面后就把餅翻身，那么這塊餅不能正好落在“鍋”中.如圖②，小麗將餅切了一刀，然后將兩小塊都翻身，結果餅就能正好落在“鍋”中.這又是為什么？

（3）如果用來烙餅的鐵皮既不是等腰三角形也不是直角三角形（如圖③），那么烙好一面后，怎樣將烙餅翻身，才能使烙餅仍能正好落在“鍋”中？

解：問題（1）學生容易根據本章學習的內容想到：因為等腰三角形是軸對稱圖形.

問題（2）畫直角三角形斜邊上的中線.因為直角三角形斜邊上的中線把直角三角形分成了兩個等腰三角形.由（1）可知，問題得以解決.

問題（3）如圖④，作△ABC的高AD，又可以把△ABC分成兩個直角三角形，由（2）可知，問題得以解決.

【評析】 本題很有趣味，主要考查軸對稱圖形的性質.問題（2）中畫出斜邊上的中線，分成兩個等腰三角形，由于等腰三角形是軸對稱圖形，分割成功.課本圖③是一個任意三角形，課本的意圖是先把三角形分成兩個直角三角形，轉化為問題（2），進而轉化為問題（1）.蘇科版教師用書給出的答案充分體現了化歸的思路（等腰三角形——直角三角形——任意三角形）.

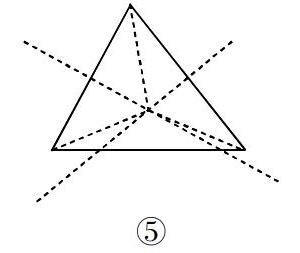
在教學過程中發現，有部分學生把問題（3）中的三角形畫成銳角三角形，于是他們去畫兩條邊的垂直平分線，其交點與三角形的三個頂點相連，得到三個等腰三角形（如圖⑤）.

因此，我們在復習時重新審視，改造成如下問題：

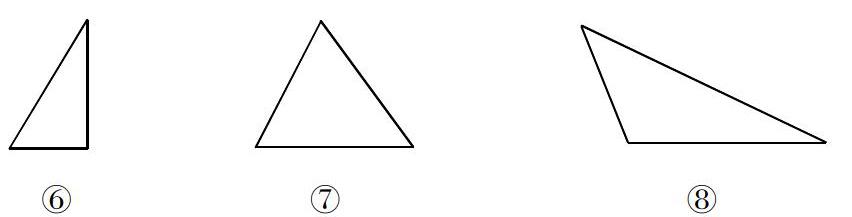
變式：（1）如圖⑥是一個直角三角形，請你把它分割成兩個軸對稱圖形.畫出分割線，說明特征.

（2）如圖⑦是一個銳角三角形，請你把它分割成若干個軸對稱圖形.畫出分割線，說明特征.

（3）如圖⑧是一個銳角三角形，請你把它分割成三個軸對稱圖形（不同于⑦中的分割）畫出分割線，說明特征.

【評析】 因為鈍角三角形時，畫垂直平分線的方法就行不通，但是有的學生（2）中用了此法，就想不到（3）中不同于（2）中的分割成三個軸對稱圖形的方法.事實上，課本中先作一條高，分成兩個直角三角形，然后畫兩個直角三角形斜邊上的中線，只要高不分割，可以分割成兩個等腰三角形以及由兩個等腰三角形拼成的四邊形，它們都是軸對稱圖形.

總 結

1. 探究活動讓學生學會學習，迅速成長；一次次體驗，讓學生自我完善，健康發展；在視野轉向生活的同時，思維得以放飛；在生活中尋求答案，讓他們的想法富有創意！探究活動的確讓師生都有了全新的體驗，激勵我們繼續尋找合適的課題開展新的探究，讓數學課堂成為探究學習的源頭活水.

2. 以問題探究課. 數學實驗課和調查研究課這些不同模式開展的研究性學習，最終的目的是幫助學生形成一種對知識主動探究、重視實際問題解決的積極的學習方式，促使教師轉變教學觀念，更加關注學生思維能力和實踐能力的培養，使他們能對所學知識加以選擇、判斷、解釋、運用，從而有所發展，有所創造.這種教育思想、方法給我們帶來的啟迪和思考是深遠的，有待于在今后的教學實踐中總結更多的經驗，以便更好地推廣實施.