以問叩學

[摘 要] 傳統數學復習課的教學模式比較單一，多以教師提問、講評和學生回答、練習為主，學生的思維易被教師所禁錮，學生的課堂主體性得不到有效體現. 把課堂還給學生，學生根據已有的認知，在教師的引導和鼓勵下，在教師創設的問題情境中發現問題、提出問題、解決問題，自主建構知識，從而打造高效的數學復習課.

[關鍵詞] 問題；復習課；高效

問題的提出

筆者有幸參與了浙江省“浙派”名師初中數學班關于復習課的八節研討課，以及浙派名師暨全國名師經典課堂教學展示的6節復習課的研討.這14節課中，或多或少地體現了把課堂還給學生，把提問題的權利還給學生，讓學生來提問題，以學定教，從而打造高效的復習課. 那么在初中數學課堂中，怎么把問題還給學生，教師又充當了什么樣的角色呢？而復習課是一種重要的教學課型，是對已學知識的再回顧、再整理、再應用和再反思，承擔著查漏補缺，夯實四基，促進學生發展的責任，是實現知識系統化，發展數學素養的核心平臺. 因此，數學復習課是數學教學中不可或缺的重要組成部分.

1. 培養學生提問題的能力的必要性

問題是數學的心臟、思維的起點（P.R.Halmos），而提出一個問題往往比解決一個問題更為重要. 在實際教學的全部過程中要始終貫穿提問的藝術. 教育家約翰·S·布魯巴克認為：“最精湛的教學藝術要遵循的最高準則是學生自己提問題. ”因此，教師在教學實踐中要注重引導學生發現問題和提出問題. 當學生自己會發現問題和提出問題的時候，數學課就不再是枯燥的思維活動了，數學教學也就充滿了趣味和活力，學生也就真正成為了學習的主體. 所以，把問題還給學生，如何讓學生“提好”問題，提“好”問題，這是值得思考的地方.

為學生創設問題情境，引導學生提出問題，有利于因材施教，使每位學生得到發展；給學生提供更多的交流、合作的機會；促進智力因素與非智力因素的協同發展；消除學生模仿解題的習慣，改進學習方法；培養學生的創新素質和探究能力，增強數學應用意識；有利于提高教學活動效率；有利于課堂開展研究性學習.

2. 當前初中數學復習課存在的問題

（1）注重知識講解，忽視學生能力. 在初中數學復習課中，有部分教師只注重知識的講解，卻忽視了學生能力的培養，從而無法真正提高復習效率. 另外，在復習課中，許多教師都是采用一刀切的復習方式，忽視了學生們存在的差異性，從而使基礎差的學生無異于聽天書. 這樣的復習無論多少遍，都是沒有效率可言的.

（2）注重題海戰術，忽視知識結構. 在初中數學的復習課中，側重于讓學生大量做練習，采取題海戰術，卻忽視了知識結構的梳理，導致整個復習雜亂無章. 這樣一來，學生因為沒有及時梳理知識結構，知識也就無法系統化，建立不起系統性的知識網絡，從而嚴重影響了知識的運用，復習效率自然也就難以提高.

（3）注重復習進度，忽視復習效率. 就初中數學而言，教學內容很多，因而教師的教學任務也很重. 等課程上完之后，已經沒有太多時間進行復習，所以許多教師就只能根據自己的教學計劃進行忙碌的復習. 而在復習課中，如果復習內容不根據學生的實際情況而進行進度上的調整的話，基本上所謂的復習就成了一個沒有多大價值的教學環節. 所謂“欲速則不達，過猶則不及”，教師在制訂復習計劃時，只注重進度，而不管實際中學生對知識的掌握情況，那么這樣的復習無疑是浪費時間，毫無效率可言.

“以問叩學”復習課案例分析

新課程改革倡導“要以學生發展為中心，把課堂還給學生”，同時數學新課程標準也認為學生的數學學習活動應當是一個生動活潑的、主動的和富有個性的過程. 在這一學習過程中，既要有效發揮教師的主導作用，又要使學生成為學習的真正主人. 把課堂還給學生，把問題還給學生，讓學生自主來發現問題和提出問題.

例1：溫州外國語學校章才岔？搖《由二次函數向動點問題漫溯》.

環節1：

師：你能否求出如圖1所示的二次函數的圖像？

生：不能.

師：需要添加什么條件？

生1：可以添加圖像與坐標軸的三個交點.

生2：可以添加頂點坐標和圖像上的另一個點的坐標.

生3：添加圖像與坐標軸的兩個交點坐標以及對稱軸直線.

……

環節2：

師：如圖2，點P（m，0）是線段OC上的一個動點，過點P做x軸的垂線，與直線BC相交于點E，與直線CD相交于點F，與拋物線相交于點Q，你能提出什么問題呢？

生4：若∠BCF=90°，求m的值.

生5：用m的代數式表示△CBF的面積.

生6：當m為何值時，△FCB為等腰三角形？

生7：當m為何值時，QF=EF？

生8：當FC=FB時，F是否為CD的中點？

生9：m為何值時，△BEF與△CFB相似？

設計意圖：本節課是二次函數的復習課，授課教師通過環節的設計，復習了二次函數的三種表達式. 通過開放式的條件添加，有利于培養學生的發散性思維，同時基于學生的學情，讓問題從學生中來，并由學生加以解決. 其中生3的提法是求不出解析式的，為什么不能求呢？學生通過思考得出結論，從而復習了拋物線的軸對稱性，因此也關注到課堂的生成. 環節2在環節1的基礎上，給出一種情況求出解析式，由鋪墊問題入手給學生創設熟悉的問題情境，以動點問題的展開作為鋪墊，讓學生感受到身邊的數學，激發學生學習數學的好奇心和求知欲. 以二次函數為載體，將簡單的動點問題分析轉化，提出待解決的問題. 當教師把提問題交給學生的時候，我們看到學生的能力是很強的，學生提出的探究線段、面積、形狀等問題，通過解決這些問題，滲透轉化、分類、方程等數學思想方法，提高學生分析問題與解決問題的能力，于潤物無聲中培養學生的數學素養. 更可貴的是章老師在最后小結的環節提煉出點動引起線動、面動，進而使圖形的形狀發生改變，使學生對動點問題的思考有了更深刻的理解，對如何來提出問題有了新的思路.

例2：中國人民大學附屬中學朝陽學校孫紅強《第三章〈實數〉小結與復習》.

環節1：師：從小學到現在，我們學習了很多數，請你寫出三個不同類型的數.

環節2：師：利用下列數據0，4，8，

3.14-π，，，-，，結合實數知識生長圖， 請你提出3個以上不同類型的數學問題.

設計意圖：環節1中一般的教師會寫出一些數讓學生進行歸類，但是孫老師是讓學生自己寫出三個不同類型的數，這樣的開放性設計能夠讓學生從實數這樣一個大的范圍對已認識的數進行分類和小結. 本節課通過類比有理數知識結構圖和無理數知識結構圖，整合形成實數知識結構圖，是本節課的一大亮點. 在環節2中，孫老師引導學生圍繞給定的數據，應用實數知識，提出問題、解決問題，加深理解實數以及相關的概念，理解在進行實數運算時，有理數的運算法則及運算性質同樣適用. 孫老師的知識生長樹不僅吸引了大家的眼球，而且使所學的知識網絡化，形成系統，是很值得大家學習和借鑒的.

例3：金華南苑中學胡艷《等腰三角形中的分類思想》.

方案1：

熱身訓練1：

（1）已知等腰三角形的腰長為4，底邊長為5，則它的周長等于______.

（2）已知等腰三角形的兩邊長分別為4和5，則它的周長等于______.

（3）已知等腰三角形的兩邊長分別為2和5，則它的周長等于______.

注意：等腰三角形是一類比較特殊的三角形，邊有腰與底之分.

熱身訓練2：

（1）已知等腰三角形的一個底角為80°，則它的頂角為______.

（2）已知等腰三角形的一個內角為80°，則它的頂角為______.

（3）已知等腰三角形的一個內角為100°，則它的頂角為______.

注意：等腰三角形是一類比較特殊的三角形，角有頂角與底角之分.

方案2：

師：（請了生1）1到10中哪個數據是你的幸運數字？

生1：7.

師：（請了生2）1到10中哪個數據是你的幸運數字？

生2：5.

師：（請了生3）你能說出一個數字，使得與前面的2個數據成為等腰三角形的三邊嗎？

生3：5或7.

師：為什么會有兩種情況？

生：等腰三角形的邊有腰和底邊之分.

師：非常好，也就是說對三角形的邊要進行分類.那么是不是一定有兩種情況呢？

生：不一定.

師：為什么？

生：要考慮能否構成三角形.

師：非常好！那誰能來舉個例子？

……

師：你能隨意地說一個0到180°之間的角嗎？

生：100°.

師：如果100°是等腰三角形的一個內角，誰能說出其余的兩個角呢？

生：40°，40°.

師：你能隨意地說一個0到180°之間的角嗎？

生：70°.

師：如果70°是等腰三角形的一個內角，誰能說出其余的兩個角呢？

生：70°，40°或55°，55°.

師：為什么有的時候是一種情況，有的時候是兩種情況呢？

生：因為等腰三角形的角分為頂角和底角，100°只能做頂角.

師：那么等腰三角形的頂角和底角有什么要求呢？

……

設計意圖：這是一節等腰三角形的復習課，對于課程的開頭片段，方案1是初稿，方案2是最后的課堂呈現，那么這兩種方案的區別在哪里呢？方案1是傳統的復習課給出形式，教師精心設計問題，從給定邊角求解，到有兩解，再到考慮能否構成三角形，檢驗兩解是否存在，歸納小結得出等腰三角形按邊、按角分類的思想. 學生按照教師的指引，按部就班地思考. 在方案2中，教師沒有指定具體的數據，而是讓學生自己來說，教師可以根據情況多舉幾個例子，學生在具體數據中感受到等腰三角形的邊角的分類，并通過感受進一步探索得出邊角分類的條件. 這種開放式的問題設計，引導學生進行探究，是打造高效復習課的重要途徑.

例4：溫州市繡山中學蔡梅園《圓的基本性質復習》.

問題1：墨子曰“圓，一中同長也”，你能用自己的語言進行解釋嗎？

問題2：在一個圓上，你添上什么能夠讓我感受到它的軸對稱性呢？

問題3：你能畫出一些與圓中的角有關的圖形嗎？

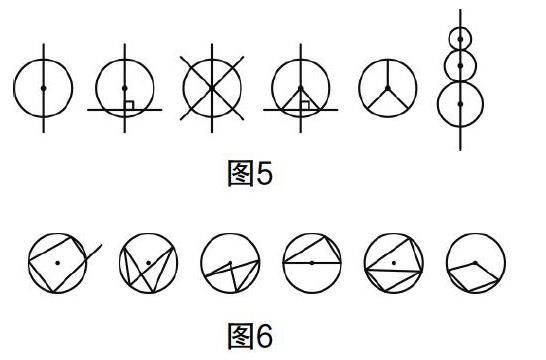
設計意圖：蔡老師在這節課中沒有像傳統的復習課一樣把知識點單獨地羅列出來，也沒有通過設計基礎題進行回顧，而是通過三個問題的設計，大膽地放手讓學生自己畫圖. 而這三個問題的設計也是非常巧妙的，第一個問題回顧了圓的半徑相等的性質，以及點與圓的三種位置關系；第二個問題復習了圓的軸對稱性，主要是垂徑定理，圖5是學生的部分作品，其中第2、4幅圖給出了垂徑定理的基本圖形，第5幅的汽車標志，以及最后的糖葫蘆，體現了學生的發散思維，更是讓學生、老師開懷大笑，活躍了課堂的氣氛；第三個問題回顧與圓有關的角，圖6是學生的部分作品，我們驚喜地發現：你給學生創造了一個舞臺，而學生卻給了你精彩的演出！學生把圓周角、圓心角、同弧所對的圓周角相等、直徑與直角的關系……演繹得非常成功，圓當中與角有關的基本圖形得到了回顧和歸納. 這樣的開放題設計不僅促進了雙基的落實，走出了“對號入座、機械模仿”的誤區，學生從不同角度進行探索，使課堂散發出生命活力！

例5：義烏繡湖中學樓春洪《二次函數背景下的面積問題》.

問題1：如圖7，已知拋物線y=x2-2x-3與坐標軸相交于點A，B，C，頂點為D，你能求出這些點的坐標嗎？能計算△ABD的面積嗎？

問題2：請你設計與點A，B，C，D，O有關的三角形面積問題并解答.

問題3：如圖8，請用盡可能多的方法來求△BDC的面積.

問題4：如圖9，當點P在第四象限運動時，你能設計哪些與面積有關的問題？

學生設計問題如下：

問題（1）：△BCP的面積為S，點P的橫坐標為t，你能求出S關于t的函數解析式嗎？

問題（2）：△BCP的面積是否存在最大值？若存在，求出點P的坐標；若不存在，說明理由.

問題（3）：以點B，C，D，P為頂點的四邊形的面積有沒有最大值？

問題（4）：△BCP的面積的取值范圍是多少？

問題（5）：若△BCP的面積為整數，這樣的點P有幾個？

設計意圖：樓老師通過問題1回顧了二次函數中的基本函數y=x2-2x-3的重要的四個點，開門見山提出與面積有關的問題，直入主題. 在問題2中通過5個點中找三個點構成三角形，滲透分類組合的思想；并在各種三角形面積的計算過程中，歸納出什么時候面積比較容易求出，對最難求的△BDC的面積如何求設計了問題3，師生共同分析得出六種解答方法，教師引導學生歸納如何擇優而選，并得出面積的三種求解方法：直接計算，通過割補法間接計算，通過添加平行線進行轉化后計算. 在問題4中，樓老師讓學生自己來設計與面積有關的問題. 事實證明，學生的出色表現把課堂推向了高潮！

“由學生提問題”對教師的要求

首先，應該轉變教育教學觀念和評價標準. “問”與“學”同等重要，不可偏廢任意一方.

其次，營造寬松、自由的教學氛圍，建立和諧的師生關系. 學生不問問題已成為當前一種普遍的現象，這并不代表學生沒有問題. 教師應該反思作為教學引導者的責任，要努力營造輕松開放的數學課堂氛圍，讓學生可以自由地呼吸. 在平時的生活中，每一段話語，每一個教學細節，都要能觸及學生的情感，走進學生的心靈，從點點滴滴做起，消除學生不敢發問的心理障礙.

再次，保護學生的好奇心，尊重問的權利. 教師不能再獨攬“問”的大權，而應尊重學生，把“問題”還給學生，把“問”的權利還給學生. 問是學的開始，是學生主動學習的一個信號，教師應該感到高興，而不是責備. 所以學生問的權利是萬不可抹殺的，而需要尊重和保護，對學生來說提問比回答問題更需要勇氣. 由于學生的知識有限，提出的問題也往往簡單，對于學生的問題，我們要表現出重視和贊賞，不能置若罔聞，挫傷學生的積極性. 不管學生提出的問題質量如何，教師都應首先肯定其提問的勇氣和努力，并及時給予引導，使其獲得“提問成功”的體驗，逐步養成勇于提問的習慣.

課堂是學生學與問的主陣地，可以利用課堂討論，促使學生提問. 要求學生互相提問題，各自的問題往往是不同的，不同的問題就產生了不同的知識體驗，因而在課堂教學中難免會存在各種“意外”的發生，這就需要考驗教師的隨機應變和駕馭課堂的能力. 教師也可以適時改變固有的教學模式，采用“提出問題—解決問題—產生新問題”的課堂結構.

總之，在學與問的關系中，我們要認識和重視問的作用，讓問題意識回歸我們的數學課堂，只有這樣，我們的學校才會走出不斷提出新問題的學生，我們的民族才會是充滿生機和活力的民族.