液力變矩器導輪葉片造型及優化設計

劉　城，閆清東，2，魏　巍，2

(1．北京理工大學機械與車輛學院，100081北京; 2．車輛傳動國家重點實驗室(北京理工大學)，100081北京)

?

液力變矩器導輪葉片造型及優化設計

劉城1，閆清東1，2，魏巍1，2

(1．北京理工大學機械與車輛學院，100081北京; 2．車輛傳動國家重點實驗室(北京理工大學)，100081北京)

摘要:為減少葉片設計參數，提高設計效率，用儒科夫斯基型線進行液力變矩器導輪葉片造型研究．對儒氏型線進行簡化，并采用尾部加厚處理，使其適應液力變矩器流動要求;構建儒科夫斯基導輪葉片型線模型，用該模型對一系列液力變矩器導輪葉片進行擬合．仿真計算與實驗結果對比表明:處理后的儒氏型線能夠精確表達已有液力變矩器導輪葉片，可以用于液力變矩器導輪葉片的設計．在集成式液力變矩器設計平臺上，利用基于存檔的小種群遺傳算法對儒氏型線液力變矩器導輪葉片進行優化，結果顯示:與傳統葉片造型方法相比，儒氏型線可以利用較少的參數有效地進行液力變矩器導輪優化設計，縮短了設計周期．

關鍵詞:液力變矩器;導輪;儒科夫斯基葉型;葉片設計;優化設計

傳統液力變矩器葉柵設計方法為基于一維束流理論的環量分配法和等角變換法．雷雨龍等［1］對傳統等動量矩設計方法進行改進，提出動量矩不等分配法進行葉片設計并對不同分配方案進行比較．葉片曲率變化較大時，此設計方法易出現較大扭曲，使設計出來的葉片制造困難．王健等［2］對葉型進行分層堆疊成型，在給定葉片角度及厚度規律的基礎上，利用等角變換將葉片展開圖映射到三維空間中構造三維葉片．使用此方法設計葉片時，設計參數過多［3］，導致優化改型比較困難．劉冀察［4］提出將儒科夫斯基型線應用到液力變矩器葉片設計中的想法，提出必須進行尾部厚度處理之后才能將儒氏型線應用到液力變矩器葉片設計中．

美國、德國、日本、韓國等汽車工業發達的國家，已經形成了一套完整的三維集成設計系統［5－6］，其葉輪機械葉柵造型方法主要分曲面造型法、曲線堆疊法和反設計法．曲面造型法是直接利用三維曲面進行葉片造型的方法，采用的曲面主要有直紋面、貝塞爾曲面和非均勻有理B樣條曲面［7－8，］;曲線堆疊法是將三維空間曲面分解為曲線進行構造的方法，主要有標準葉型函數法、葉片骨線加厚度分布構造法和吸力面壓力面構造法3種［9－10］;反設計法是由給定的流場狀態參數分布反求出葉型幾何的方法，主要有二維反設計法和三維反設計法［11］．

隨著計算能力的提高及計算流體動力學(CFD)技術的發展，三維流場仿真可以應用到葉柵系統設計中．新型的液力變矩器三維流動設計對三維葉片造型提出了新的要求［12－13］．理想的葉片構型方法應盡量滿足以下3點要求: 1)型線靈活容易調整，具有較好的適應性及魯棒性; 2)約束條件可以靈活地處理，工藝及形狀約束易于施加; 3)設計變量盡可能少．

葉柵幾何描述方法十分重要，關系到后續計算過程的效率高低和葉柵綜合性能的優劣［14］．儒科夫斯基型線具有如下優點: 1)全葉型可解析，精度高，便于CAD中應用; 2)曲率連續，沒有突變，流線光滑; 3)控制參數少，只需兩參數即可進行葉型構造．

本文探索將儒科夫斯基型線用于液力變矩器導輪葉片設計的方法，首先，簡化了儒科夫斯基型線表達式，并在其基礎上進行尾緣加厚處理;隨后，利用該型線對已有液力變矩器導輪葉片進行擬合，并利用CFD對其性能進行計算并與實驗結果進行對比;最后，在CFD仿真基礎上利用遺傳算法對儒氏導輪液力變矩器進行優化，驗證了儒科夫斯基型線導輪設計的可行性和實用性．

1　儒科夫斯基型線概述

儒科夫斯基變換是保角變換中一個十分重要的變換函數，在研究理想流體平面勢流運動中，應用該變換可以將復雜的繞翼型流動變換為簡單的繞圓柱流動．由圓柱流動ζ平面向型線z平面的儒可夫斯基變換解析函數具有如下形式:

式中常數C為實數．

如圖1所示，對ζ平面中圓心位于第二象限的圓進行儒科夫斯基保角變換，即可得到z平面中的儒科夫斯基型線．其中ζ平面中圓心與虛軸(η軸)的距離與型線厚度(t)有關，圓心與實軸(ξ軸)的距離與型線的彎度(h)有關，弦長(s)與實數C有關，儒科夫斯基型線的表達式為

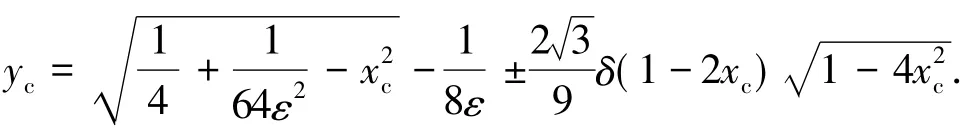
式中:δ=t/s，稱為相對厚度;ε=h/s，稱為相對彎度; yc為型線相對于弦長的量綱一的縱坐標; xc為型線相對于弦長的量綱一的橫坐標．式中:±前表達式為型線中弧線，取正號時表示上型線，取負號時表示下型線．對該式關于ε進行泰勒級數展開并進行坐標變換，忽略3次以上高階量后得［15］

式(1)為弦長s=1、前緣在原點處的型線，且中弧線最大彎度為ε，最大厚度為δ．

由圖1可知，用式(1)設計的葉片型線具有尖尾緣，而液力變矩器導輪往往是鑄造成型，而尖銳的尾緣無法鑄造，所以必須對該方法進行改進．文獻［12］中提出加一個厚度項來構造光滑尾緣儒科夫斯基型線的方法，表達式為

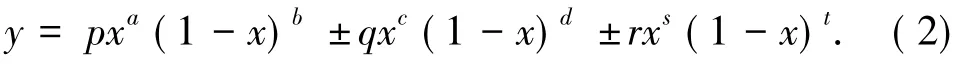
式中:上型線為式中“±”均取“+”;下型線為式中“±”均取“－”; p為控制型線中弧線彎度項; q為控制型線厚度項; r為控制尾部加厚項，為主要控制參數，且一般有r＜q，s≥d，t≈c，各系數均為正數; a、b、c、d、s、t為微調參數，可以調節型線頭部和尾部的收縮、升降等．經過對一系列導輪葉片進行統計研究表明，r取值0．05～0．10，s取值2～3，t取值0．2～0．5．

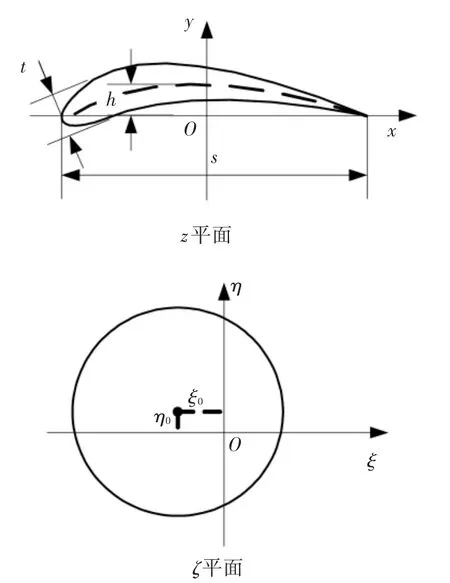
圖1　儒科夫斯基變換

2　儒氏型線導輪葉片設計及擬合

儒科夫斯基型線具有鈍頭前緣，比純粹圓弧更為合理，特別適合于大頭導輪葉片的構型．對單元儒科夫斯基型線進行旋轉、縮放，即可獲得需要的導輪平面葉型，最后，利用多圓柱面投影將二維葉片型線投影到三維，進行葉片三維實體的構造．

如圖2，對單元儒科夫斯基型線進行旋轉，可得到相應姿態的“單元導輪型線”，再對此型線進行縮放即可得到導輪型線．導輪型線的姿態由旋轉角(β)決定．

圖2　旋轉單元儒科夫斯基型線

為驗證儒氏型線是否能對已有葉片進行表達，對初始導輪型線作逆向旋轉、縮放處理，可獲得“單元導輪型線”，隨后可用儒氏型線對其進行擬合．設獲得的原始“單元導輪型線”上、下型線離散點為(xi，yi)，i=1，…，n，n為離散點數量．上型線φs和下型線φd的表達式為

式中: ps、qs、pd、qd為待求系數．根據最小二乘法原則，所求系數應使誤差平方和最小，即

取極小值．由極值定理，可得以下求解方程組:

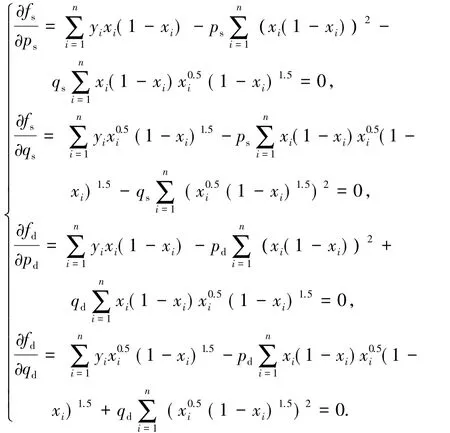
由以上方程組可解出最小二乘法擬合的儒科夫斯基型線彎度和厚度系數，同時，利用光滑尾緣儒科夫斯基型線的表達式(式(2) )對其進行尾緣光滑修正，獲得擬合后導輪內、外環曲線．選取D265、D315 及D400 3組液力變矩器導輪葉片，利用儒氏型線對其內、外環型線進行擬合，將擬合結果與原始型線進行對比，結果見圖3～5．

由圖3～5可知，D265導輪葉片頭部較大，彎度較小; D315導輪葉片彎度較大; D400導輪葉片具有較大彎度，但是葉片較狹長，頭部較平．擬合結果對比可知，擬合誤差主要出現在葉片首、尾部．其中D400內環導輪型線用儒科夫斯基型線擬合時在頭部出現最大誤差，誤差絕對值在0．015以下．以上所有導輪儒氏型線擬合誤差均方根在0．008以內，標準偏差在0．007以內，擬合結果證明儒氏型線對不同特征導輪葉片均能較精確的表達．

圖3　D265液力變矩器導輪型線擬合結果

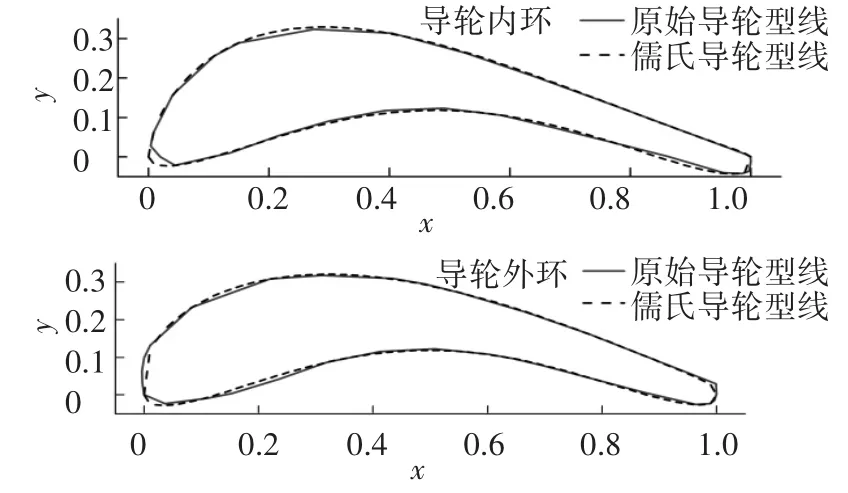
圖4　D315液力變矩器導輪型線擬合結果

圖5　D400液力變矩器導輪型線擬合結果

3　儒氏型線導輪葉片三維造型及性能預測

選取有效直徑為400 mm的D400型液力變矩器為原型，利用多圓柱面投影法對儒科夫斯基型線進行三維映射，得到三維導輪葉片并與原始葉片進行對比(見圖6)，由圖6可知，儒科夫斯基型線對原始導輪有較好的擬合效果．

圖6　三維導輪葉片對比

采用全流道模型，在網格獨立性分析基礎上，利用非結構網格對流道進行空間離散，單個葉輪網格數約為300萬，計算模型總網格數為900萬．利用剪應力輸運方程(SST)模型，對儒科夫斯基導輪液力變矩器進行牽引工況下(i=0～0．8)三維流場計算，其計算模型如圖7．將原始液力變矩器及儒氏導輪液力變矩器計算結果進行對比，結果見圖8及圖9．

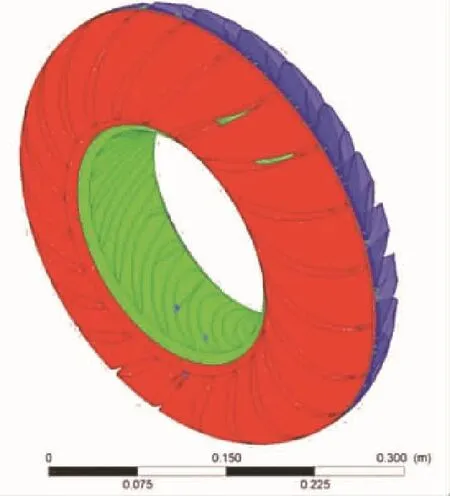
圖7　液力變矩器全流道CFD計算模型

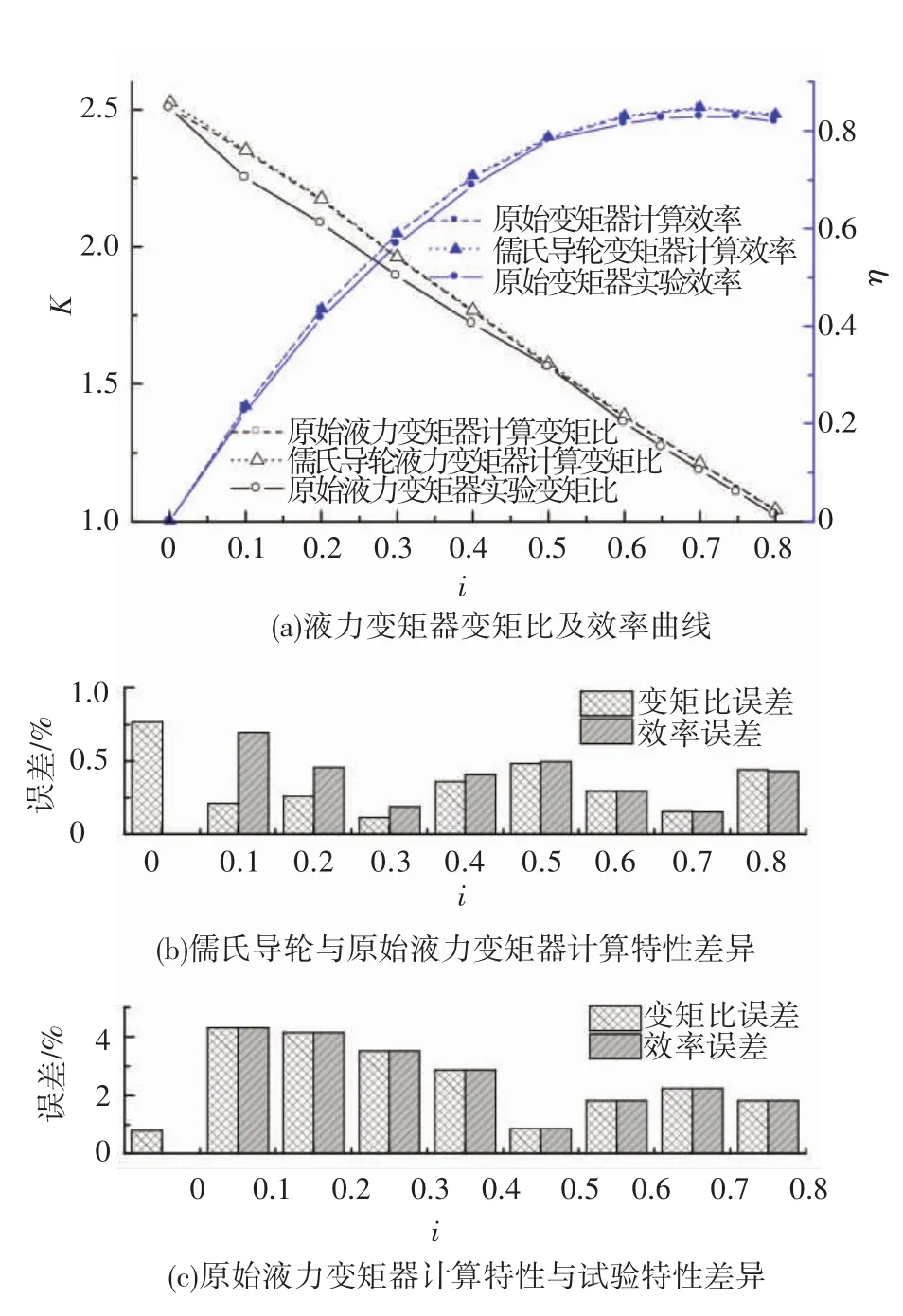
圖8　變矩比及效率計算結果對比

圖8、9中誤差柱狀圖為原始液力變矩器與儒氏導輪液力變矩器計算結果的誤差，同時原始液力變矩器實驗數據及誤差也在曲線圖中給出．由原始液力變矩器與儒氏導輪液力變矩器計算結果對比可知，儒氏導輪變矩比及效率的計算結果與原始液力變矩器吻合度較高，特性曲線幾乎重合(見圖8(a) )，儒氏導輪液力變矩器計算數值要比原始稍高，但誤差均在1%以內(見圖8(b) ) ;儒氏導輪計算泵輪扭矩系數較原始導輪小(見圖9(a) )，但誤差也在2%以內(見圖9(b) )，誤差主要出現在高速比區域．由于D400導輪葉片內環型線頭部較平，用儒氏葉型對其擬合時在頭部出現較大誤差(圖5)，內環處導輪頭部的差異是導致計算結果誤差的主要因素．同時，原始液力變矩器的實驗特性也在圖中顯示，兩種CFD計算結果與實驗結果較吻合，效率與變矩比誤差在5%以內(見圖8(c) )，泵輪扭矩系數誤差在6．5%以內(見圖9(c) )，驗證了全流道CFD計算的準確性．

圖9　泵輪扭矩系數計算結果對比

4　基于遺傳算法的液力變矩器導輪葉片優化

利用程序實現儒氏導輪葉片的參數化生成，采用批處理、腳本文件實現液力變矩器三維流場仿真過程的自動化，搭建基于三維流場仿真的液力變矩器設計計算平臺［16］，為縮短優化周期，采用周期性穩態CFD計算作為特性預測手段來優化葉柵參數．選取內環旋轉角(βin)、外環旋轉角(βout)、內環彎度pin、外環彎度pout、內環厚度qin、外環厚度qout作為設計變量，最高效率(ηmax)及泵輪起動力矩系數(λB0)指標作為目標函數，起動變矩比(K0)作為約束，建立導輪六變量多目標優化模型:

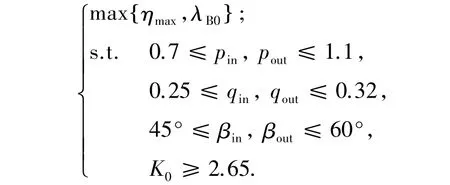
采用基于存檔的小種群遺傳算法(AMGA)對儒氏導輪液力變矩器進行多目標優化．AMGA算法采用較大的外部存檔保留精英解，可使用小種群獲得大量非劣解，從而減少適應值評估次數，降低計算量，其采用擁擠距離算法保證解的多樣性，同時利用懲罰函數對約束進行處理，具有較強的全局搜索能力［17］．

利用AMGA算法直接在自動化液力變矩器設計計算平臺上尋優，共計算280個樣本點，其中獲得256個可行解，62個非劣解．圖10給出優化后的結果與初始值的對比．由圖10可知，優化后，液力變矩器獲得一系列的非劣解，設計人員可以根據實際需要在這些設計中進行權衡、選擇．

表1中1～3為選取的3組典型非劣解，0組為初始解．由表1可知，經過優化后，設計人員可以在一系列不同性能的液力變矩器中進行選擇，其中No．1解具有較高的效率，但是其能容較低; No．2解以犧牲經濟性為代價提高了功率密度; No．3解綜合了效率及功率密度兩項指標，雖然單項指標并非最優，但是經過優化后液力變矩器動力性及經濟性較初始解有所的提高．

圖10　多目標優化結果

周期性穩態流場計算速度雖然快，但精度相對較低，為提高設計精度，利用全流道CFD模型對優化結果進行驗證，得到精確的優化后液力變矩器特性及誤差(見表2)，其誤差值為周期性流道優化結果與全流道模型計算結果．由表2可知，利用儒科夫斯基導輪，結合CFD仿真，可以對原型液力變矩器進行有效優化．

表1　三組典型非劣解

表2　優化結果全流道模型驗證

5　結　論

1)通過變換并加入尾部加厚項處理，可以使儒科夫斯基型線適應液力變矩器導輪葉片設計的需要．

2)型線誤差及CFD計算誤差結果表明，儒氏型線能夠精確表達原始導輪．

3)編制了參數化儒科夫斯基型線導輪葉片設計程序，并結合自動化液力變矩器三維流場設計分析平臺，利用遺傳算法對儒氏導輪進行優化．優化結果表明No．3與原型在各性能指標上均有所提高，同時獲得了不同性能的非劣解可滿足不同使用需求，驗證了儒氏型線應用于液力變矩器導輪葉片設計的實用性．

4)傳統的葉片造型方法一般需要至少25個參數對葉片進行表達［18］，而儒氏導輪只需要6個參數即可對型線進行完整表達，大大減少了設計變量，從而縮減了設計周期．

5)對厚度項進行處理后，儒科夫斯基型線也可能應用于液力變矩器渦輪及泵輪的葉片設計，該應用仍有待進一步研究．

參考文獻

［1］雷雨龍，王健，胡延輝，等．液力變矩器葉柵動量矩分配規律［J］．吉林大學學報(工學版)，2009，39(4) : 880－884．

［2］王健，葛安林，雷雨龍，等．液力變矩器葉片三維成型法及其性能分析［J］．吉林大學學報(工學版)，2007，37 (1) : 43－47．

［3］魏巍，劉城，閆清東．柔性扁平循環圓液力元件葉柵系統設計方法［J］．農業機械學報，2011，42(4) : 33－37．

［4］劉冀察．儒科夫斯基翼型用于液力變矩器葉型設計的研究［J］．工程機械，2003(1) : 22－24．

［5］KYOUNG S，KYUSUP K，JAEIN P．Development of the integrated process for torque converter design and analysis ［C］/ /Proceedings of 2008 SAE World Congress．Detroit: SAE International，2008: 0785．

［6］ABE H，MASAAKI T，AKIO M．Development of super ultra flat torque converter with multi plate lock-up clutch ［J］．SAE Int J Engines，2009，2(1) : 48－55．

［7］HAZEN F，ABDEL H．Incorporation of sweep in a transonic fan design using a 3D blade-row geometry package intended for aero-structural-manufacturing optimization ［D］．Monterey: Naval Postgraduate School，1997: 32－35．

［8］ROSSGATTERER M，JUTTLER B，KAPL M．Medial design of blades for hydroelectric turbines and ship propellers［J］．Computers＆Graphics，2013，36(5) : 434－444．

［9］OZHAN O，IBRAHIM S．Multi-objective aerodynamic optimization of axial turbine blades using a novel multilevel genetic alorithm［J］．Journal of Turbomachinery，2010，132(1) : 0411009－1－14．

［10］DAMIR V，ZELJAN L，IGOR P．Computational procedure for optimum shape design based on chained bezier surfaces parameterization［J］．Engineering Applications of Artificial Intelligence，2012，25(3) : 648－667．

［11］MAHDI N，FARZAD P．Optimization of a seven-stage centrifugal compressor by using a Quasi-3D inverse desigh method［J］．Journal of Mechanical Science and Technology，2013，27(11) : 3319－3330．

［12］GEORGIA K，SOTIRIOS S，IOANNIS N．A software tool for parametric design of turbomachinery blades［J］．Advances in Engineering Software，2009，40(1) : 41－51．

［13］YAN Qingdong，LIU Cheng，WEI Wei．Numerical simulation of the flow field of a flat torque converter［J］．Journal of Beijing Institute of Technology，2012，21(3) : 309－314．

［14］DERKSEN W，TIM R．Bezier-PARSEC: An optimized aerofoil parameterization for design［J］．Advances in Engineering Software，2010，41(7) : 923－930．

［15］姜海波，趙云鵬．基于中弧線－厚度函數的翼型形狀解析構造法［J］．圖學學報，2013，34(1) : 50－54．

［16］劉城，潘鑫，閆清東，等．基于DOE及RSM的液力變矩器葉片數對性能的影響及優化［J］．北京理工大學學報，2012，32(7) : 689－693．

［17］SANTOSH T，PATRICK K．AMGA: an archive-based micro genetic algorithm for multi-objective optimization ［C］/ /Proceedings of 2008 Genetic and Evolutionary Computation Conference．Atlanta: Computer Science Curriculum Press，2008: 729－736．

［18］魏巍，閆清東．液力變矩器葉柵系統樣條擬合參數設計體系［J］．農業機械學報，2009，40(2) : 22－26．

(編輯楊波)

Design and optimization of torque converter stator blade

LIU Cheng1，YAN Qingdong1，2，WEI Wei1，2
(1．School of Mechanical Engineering，Beijing Institute of Technology，100081 Beijing，China; 2．National Key Lab of Vehicular Transmission(Beijing Institute of Technology)，100081 Beijing，China)

Abstract:In order to reduce design parameters and shorten design cycle，Joukowksky profile was utilized to construct torque converter stator blade．By simplifying the Joukowksky equation and adding a thickness term to its end，the Joukowksky stator blade model was given．According to fitting results，Joukowksky is able to present the existing stator blades and hence is suitable for stator blade design．Afterwards，the archive-based micro genetic algorithm was employed to optimize the Joukowksky stator blade based on an integrated 3D blade design system．The results indicated that the Joukowksky profile could be used in stator blade design with less parameters and the performances were improved after the optimization．

Keywords:torque converter; stator; Joukowksky profile; blade design; design optimization

通信作者:閆清東，yanqd@ bit．edu．cn．

作者簡介:劉城(1986—)，男，博士研究生;閆清東(1964—)，男，教授，博士生導師．

基金項目:國家自然科學基金項目(51475041)．

收稿日期:2014－11－07．

doi:10．11918/j．issn．0367-6234．2016．01．017

中圖分類號:TH137．332

文獻標志碼:A

文章編號:0367－6234(2016) 01－0114－06