數形有機結合關系自然求聯
——《平面圖形的面積關系》教學設計與思考

張翼文（特級教師）

【教學目標】

1.知識技能：通過已學知識梳理，學生能自主地解答長方形、平行四邊形、三角形與梯形面積的問題。

2.數學思考：通過經歷畫畫、說說、想想等數學活動，學生能主動理解梯形的面積公式對于長方形、平行四邊形、三角形的面積計算也是適用的。

3.問題解決：通過對長方形、平行四邊形、三角形與梯形的面積公式的溝通，學生能主動地解決一些相關問題，以此促進數學推理能力的提升。

4.情感態度：通過數學探索活動，學生感受事物間的相互聯系，并體驗數形結合看問題的內在魅力，從而激發數學學習的興趣。

【教學過程】

一、出示課題，談話引入

師：今天我們一起來研究《平面圖形的面積關系》，你看了這個課題后，你覺得哪個詞是這節課的關鍵詞呢？（板書：平面圖形的面積關系）

生：我認為應該是“圖形”。

生：我認為應該是“關系”。

生：我認為應該是“面積”。

師：同學看法不一致，那怎么辦？

生：往下學習就可以知道了！

師：那我們就往下研究即可知。

【設計意圖：課堂伊始，師生圍繞課題進行簡單對話，既能集中學生注意力，又能喚起探索的心向與欲望。】

二、回顧梳理，主動探索

1.知識的簡單回顧與梳理。

（1）媒體出示，并說一說以下幾種平面圖形的面積計算公式。

（2）梳理展示。

S長方形=a×b

S平行四邊形=a×h

S三角形=a×h÷2

S梯形 =（b+a）×h÷2

（3）問題暗示，引入探索。

師:這幾個平面圖形的面積計算過程中，你覺得哪個相對麻煩些呢？為什么？

生：我們認為梯形的面積計算相對麻煩些，因為，計算的步驟會多些。

師：今天就從計算相對比較煩的梯形面積公式開始研究，看能否給我們帶來什么啟示？

【設計意圖：本環節對原有的幾種平面圖形的面積計算的知識進行簡單回顧與梳理，這樣面向全體的活動，可以夯實學生基礎，起到溫故而知新的效果。同時，在師生對話交流過程中，教師具有一定傾向性的問題暗示，可以進一步激發學生的探索欲望，為課堂后續學習注入熱情。】

2.任務驅動，實踐操作。

（1）任務驅動。

活動要求：請在下面格子圖內畫出高為4厘米，面積為20平方厘米的梯形。

（每個小正方形的邊長為1厘米。）

（2）自主實踐。（略）

（3）匯報交流。

師：完成這個作品前，你們是怎么想的呢？

生：我是用梯形公式倒過來推算的，求出梯形的上下底之和（即面積20乘2除以高4，得到上下底之和為10），然后確定上底為4，下底為6，最后再畫的。

（4）展示作品。

師：老師也準備好這四幅作品，為了便于看清楚，老師已經按等比例擴大。

（逐一把四幅作品展示黑板上）

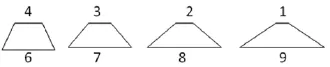
【設計意圖：本環節通過畫梯形這一任務驅動，促使學生對計算梯形面積相關知識的有意回憶，過程中學生進行有序地思考，學習任務完成的過程即思行合一的過程，進一步使學生知其然亦知其所以然。】

三、問題驅動，溝通聯系

1.對話感知，引發思考。

師：上下底之和為10，高為4的梯形，只能畫出這四幅作品嗎？

生：如果梯形上下底的長度不一定是整數，可以是小數的話，那就有很多可能？

師：你們明白他剛才說的意思嗎？你們能舉例說明嗎？

生：上底為3.5,下底為6.5,高為4。

生:上底為1.8,下底為8.2,高為4。

……

師:有多少種呢?

生:有無數種情況。

……

【設計意圖：此環節通過啟發式的引導，順其自然地促進學生解決問題所需采集的數據從整數向小數延伸，伴隨著學生的思維就由局限走向開放，彰顯了課堂動態推進的過程中變與不變、有限與無限的關系。】

2.問題跟進，素材展現。

師：如果老師也來說幾種，可以嗎？

生：贊同！

師：上底為 0.9，下底為 9.1，高為 4；（實物展示黑板上，并標把上下底數據標上）

上底為0.8,下底為9.2,高為4;

上底為0.2,下底為9.8,高為4;

上底為0.1,下底為9.9,高為4。

……

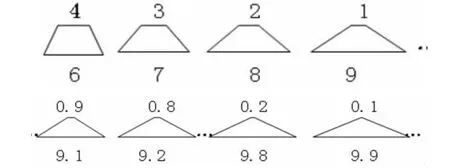
【設計意圖:此環節通過師生對話，教師適機有選擇地展現一些梯形,并標有相關數據,為接下來,學生進行長方形、平行四邊形、三角形與梯形的面積計算公式進行有效溝通提供直觀的素材。換句話說，也就是要促進學生思維走向深刻是需要教師幫助學生搭建“腳手架”的。】

3.數形結合，觀察發現。

師：請仔細觀察以上一組梯形，你有什么發現，或有什么想說的嗎？

生：從左往右看，我發現梯形的上底越來越短，下底越來越長。

生：從左往右看，我發現梯形越來越像三角形了。

師：大家都觀察到了嗎？

（學生點頭默許）

師：你們是怎么看出來的呢？

生：我是從并排梯形樣子看出來的。

生：我發現，如果梯形上底越來越短，越來越短，它就會變成三角形。

生：我不太同意他的觀點，因為梯形上底盡管越來越小，越來越小，但是再小，還是有長度的，只是我們看圖形像三角形，實際上還是梯形。

師：你們同意他的觀點嗎？

（學生點頭表示同意）

師：你們很會觀察與思考，這正如華羅庚先生所說“數缺形少直觀，形缺數難入微”。如果我們單從形看，越往右的梯形肉眼看就是三角形，如果看上下底提供的數據來看，哪怕上底越來越小，但是它還是梯形，只有當數與形結合起來看，我們來分析問題就會更合理。

……

【設計意圖：從環節中可以看出，學生在課堂中精彩對話源自于適合的素材，本環節提供一組上下底標有變化數據的梯形實物圖，幫助學生可以數形結合進行有效觀察，并發現梯形與三角形之間的微妙關系，以此適機進行梯形面積公式適用于三角形的面積計算的有效溝通。以此真正意義上落實“數缺形少直觀，形缺數難入微”之數形結合幫助學生進行合情推理的課堂教學理念。】

4.適機整合，溝通聯系。

（1）引導溝通。

師：大家剛才發現，越往右梯形的上底越來越小，如果我把梯形上下底標上字母（在展示的圖形上標出）。上底越來越小，也就是上底A點與B點慢慢逼近，AB點之間的距離越來越小，距離越來越接近“0”，如果 AB點距離為“0”時，那梯形就成為三角形；這時候三角形的面積可以怎么計算呢？

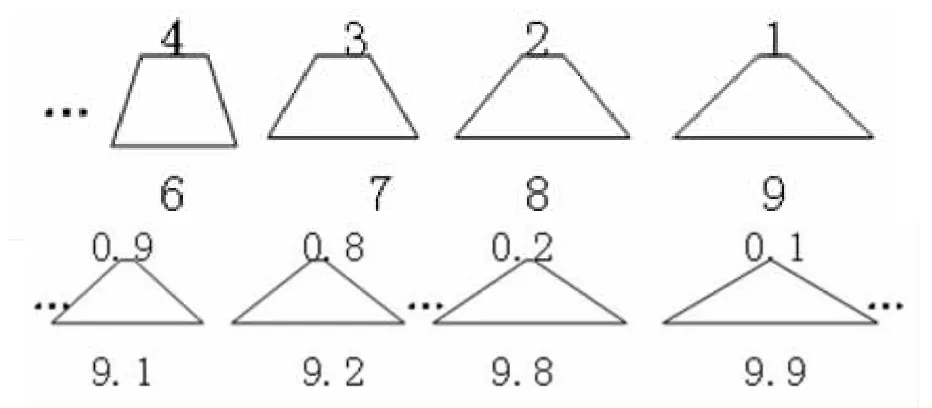
生：（0+10）×4÷2。

（2）自主求聯。

師：梯形的面積公式也適用于三角形的面積。

（并規范板書 S三角形 =（b+a）×h÷2(b=0)）

（3）整體求聯。

師：從左往右來看以下梯形的上底不斷變長，如果繼續增長，梯形又可能變成什么圖形呢？

生：平行四邊形。

師：那么梯形的面積也適用于平行四邊形。

（板書示意溝通梯形、三角形、平行四邊形、長方形的面積關系圖）

（4）適機點題。

師:到現在為止,你明白這個課題的關鍵詞應該是什么呢?

生:應該是“關系”！（異口同聲地說）

【設計意圖：此環節通過適當的問題驅動，引領學生靜態觀察與動態思考，從而促進梯形面積公式適應于三角形、平行四邊形與長方形的面積計算進行“無縫”對接，正如蘇格拉底所描寫的教師好似“助產師”，教學行進過程中不斷助推學生的學習引向深處。】

四、學以致用，解決問題

1.基礎性練習。

下面四個圖形的面積相等，另外三個圖形的底是多少？（口答）

2.實踐性練習。

（1）在上底為8，下底為10的梯形中添上一條線，使它分成兩個面積相同的部分，你有幾種不同的畫法？并用數據表示出結果。

（2）把上底為8，下底為10的梯形分成面積相等的平行四邊形、三角形與梯形的三部分，你能完成嗎？并用數據表示出結果。

3.綜合性練習。

拓展題：求出陰影部分的面積

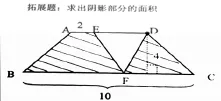
【設計意圖：練習設計應該體現一定的層次性和靈活性。目的之一是夯實學生的基礎，基礎知識和基本技能是學生發展的根本，教學中不能淡化；另一方面讓學生的思維走向深刻，著眼學生的后續發展。】