“根”深才能期待“葉”茂
——《分數加減法》教學

張國良

【背景說明】

人教版教材《分數加減法》內容的編排分兩個學段。一是三年級上冊《分數的初步認識》之后，教材編排了簡單的分數加減計算，旨在通過具體加減計算，借助數形結合，加深學生對分數“幾個幾分之一”的認識，一般不涉及到計算方法的歸納提煉；二是五年級下冊，學生認識了分數的意義，了解分數單位之后，教材編排了《同分母、異分母分數加減法》，對分數加減法的算法與算理進行系統歸納。學生在三年級學習簡單分數加減法的基礎上，已經掌握了簡單的同分母分數加減法的計算方法，結合簡圖也能初步理解算理。故而，如果再按教材的編排，將《同分母分數加減法》單獨上成一課時，甚至兩課時的話，那么完全就是三年級的“低效重復”，而非“遷移生長”。因此，本課的目標定位不再是簡單地讓學生掌握同分母分數加減法的計算方法、明確算理，而是通過對整數、小數、分數加減法三者算理的溝通，尋求“加減法”計算的本質，從而在完成異分母分數加減法教學時，讓學生實現遷移。

【教學過程】

一、揭題——明確學習任務

師：今天這節課，老師要和同學們一起學習分數的加減計算。我們在三年級的時候已經學過了類似“”這樣的分數加減法，這節課我們不但要進一步學習分數加減法的計算方法，掌握算理，還要研究分數加減法與整數加減法、小數加減法的聯系。先請同學們完成下面四題的計算。

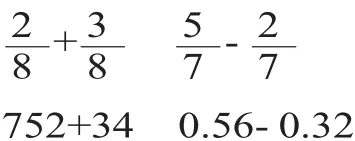
【設計意圖：基于學生的實際起點，將簡單的同分母分數加減法和整數、小數加減法同時呈現，讓學生復習計算，并開門見山告知學生本節課的學習目標，既為學生提供學習素材，又讓學生明確研究方向。】

二、培“根”——對比溝通整數、小數、分數加減法算理本質

1．喚醒經驗,歸納同分母分數加減法的計算方法。

（完成上面四題的計算、校對后，師生歸納）

師：像這樣的同分母分數加減法，我們怎么計算？

生：分母不變，分子相加或相減。

師：為什么可以這樣算呢？你能結合加法說說這樣算的道理嗎？

師：原來分母相同，就是分數單位相同，所以可以直接分子相加減。

【設計意圖：通過設問同分母分數加減法的計算方法，師生共同歸納計算法則。在此基礎上追問算理，喚醒三年級簡單分數加減法的學習經驗，為溝通整數、小數、分數加減法的算理，尋求計算本質奠定基礎。】

2.首次比較，溝通整數、小數加減法計算的本質。

師：整數、小數、分數加減法是否存在著相同的地方？哪些地方相同呢？我們先一起來比一比整數加減法和小數加減法相同的地方。

生：都要相同數位對齊。

師：相同數位對齊代表著相加或相減的兩個數的什么相同？（生：計數單位）只有計數單位相同，才能相加減。

師：計數單位相同的兩個數相加減后，所得結果的計數單位有沒有變？（生：沒有）實質上相加減的是什么？

生：相加減的是計數單位的個數。

師：的確，不管是整數加減法還是小數加減法，它們計算的實質是一樣的，就是計數單位始終不變，相加減的就是計數單位的個數。

3．再次比較，溝通整（小）數加減法與分數加減法的計算本質。

師：整數（小數）這一類加減法和分數加減法，它們是否也存在著相同的地方呢？請討論交流。

生：分數單位也是計數單位，分數單位相同，可以直接相加減。

生：整數、小數在加減時，計數單位是不變的，分數加減法計算時，分數單位也不變，也就是分母不變。

生：整數、小數在加減時，把計數單位的個數相加或相減，分數加減時，就是把分數單位的個數相加減，也就是分子相加減。

教師根據學生回答，進行梳理，形成板書如下：

【設計意圖：上述尋“根”環節，讓學生“回憶——比較——類化”，幫助學生歸整梳理，形成系統。在類比的過程中，安排兩個步驟：先是通過整數加減法和小數加減法的比較，讓學生明白加減的實質是“分數單位不變，分數單位的個數相加減”，然后引導學生將已同化的整數、小數加減法與分數加減法再次比較，尋找三者之間的本質聯系。這樣的教學條理清晰，既在學生的學習能力范圍之內，又不限于學生的表面重復，是組織學生對加減計算本質的理解和“根源”的明確，使得接下來學生異分母分數加減法的遷移水到渠成。】

三、長“葉”——遷移完成異分母分數加減法計算教學

2.學情呈現。

3.反饋交流。

師：上面解決異分母分數加減法的這幾種方法，有什么共同的地方？

生：都進行了轉化。

生：都轉化成了小數計算，或者轉化成同分母分數后再計算。

師：為什么要轉化？

生：因為轉化前分數單位不同，不能相加減。轉化后計數單位相同了，就能相加減了。

生：轉化成小數后，計數單位都變成了0.1，轉化成同分母成了或。

……

4.回顧總結。

師：這節課你有什么收獲？

生：我知道了分數加減法的計算方法。

生：整數加減法、小數加減法和分數加減法是有聯系的，加減的實質就是“計數單位不變，計數單位的個數相加減”。

生：知識之間是有聯系的。我們要經常試著理理知識之間的聯系，這樣可以使我們學得更扎實……

【設計意圖：“根深”方能“葉茂”。通過對整數、小數、分數加減法算理的比較，學生明白“只有計數單位相同，才能相加減”，加減計算的本質是“計數單位不變，計數單位的個數相加減”。有了這樣的認知基礎，學生對異分母分數加減法的計算順利實現遷移。這樣教學，教師就把“算理溝通”板塊上扎實了，就等同于激活了原先種植在學生心中的那顆優質良性的“種子”，使其發芽茁壯。后面的異分母分數加減法教學，其實就是對同分母分數加減法的豐富拓展，是“枝葉”的自然生長。因而，本課的教學側重點也與傳統教學有了區別，不再是異分母分數加減算法與算理的單一理解，而是在學生的心中構建起一個完整的知識體系。】

【課后思考】

在著名特級教師俞正強老師的《種子課——一個數學特級教師的思與行》一書中這樣論述：如果將某一知識系統作分數加減法后，分數單位都變為一棵樹，這棵樹的生長過程表現為若干節“課”，那么，一定有一些課需要“蒔也若子”，充分理透脈絡；一定有一些課可以“置也若棄”，讓學生充分自主。“蒔也若子”的課，通常處于起點或節點，謂之“種子課”；“置也若棄”的課，通常處于點與點之間，謂之“生長課”。

一、“種子課”的深刻，造就“生長課”的簡約

“生長課”的前生是“種子課”，種子的力量在于生長。在俞正強老師的書中說到，我們要精心設計“種子課”的每一個環節，把它上成可供遷移、可供生長的關鍵課，要把知識的種子埋在學生的心里，努力讓它生根發芽，獨立生長。的確，“知所先后，則近道矣”，數學教學如同打仗，一定要打好關鍵的幾仗，關鍵的幾仗打好了，就成形成勢，其他仗就能勢如破竹般地獲得勝利。在實際教學中，對于整數加減法和小數加減法算理的理解，我們一般要求學生理解到“相同數位對齊，即計算單位相同才能相加減”，極少挖掘到加減的實質是“計數單位的個數相加減”。而在本課中，教師引導學生真正關注加減計算的實質，讓學生在已有的認知基礎上再往前邁一小步，真正明確知識的根源。通過觀察、思考、比較，學生感悟到整數、小數、分數加減法的計算實質是相同的，即“分數單位不變，分數單位的個數相加減”，這樣深層次的理解，讓學生在學習異分母分數加減法時，有了學習的參照，一切變得游刃有余。因而，只有“種子課”上深刻了，非基點或非節點的課才有可能鼓勵學生自己閱讀、自己思考，才能造就“生長課”的簡約。

二、縱觀全局，謀劃“生長課”的教學策略

1.深刻解讀教材，探尋“生長課”的“前世今生”。

設計好一節課需要關注教材體系。每一節課的教學都應該從系統的角度來思考，整體把握一個知識塊的前生、今世及后延。眾所周知，學習知識的過程一定有其發生的基點、發展的節點，這些基點與節點就是“種子課”，要花力氣加以精雕細琢。同時，作為“種子課”的后延，教師也應明確“生長課”的“前世”，在組織教學時，該回憶的地方要回憶，該喚醒的地方得喚醒，該比較的地方比較，該追問的地方追問，確保教學不是簡單的重復，而能有新的“生長”。

2.了解學生起點，明確“根”源。

“種子課”的真正意義，就是將數學知識植根于學生的經驗之中。這樣，學生的所有經驗都將成為“種子課”成長的“根”源，才會支撐“種子的芽”的生長。因此，學生的認知起點是教師教學的出發點，教師不僅要了解教材的編排體系，更應了解學生已經知道了什么，并充分利用它，使它生長。所以，我們在設計一節非“種子課”的時候，應該思考學生心目中的“種子”有哪些，是什么？這些“種子”怎么激活？它的后延又可以到哪里，應該長成什么樣？等問題。

3.注重比較，凸顯本質。

“種子課”理論的核心是“遷移”，即需要教師整體著眼、前后貫通、點面結合，幫助學生打通知識之間的聯系，形成體系，串珠成鏈，其中“比較法”是非常有效的教學方法。教師可以組織學生對新舊知識間的異同進行比較，從而挖掘知識的本質，達成遷移同化，將新的知識納入原有的知識體系。相對于“生長課”后期的“比較”，“種子課”先前對于數學本質的挖掘，于教師來說是一個難點。正如，“分數加減法”的教學，如果前期對整數、小數加減實質的挖掘不到位，那后面的“遷移生長”也就無從談起。

4.適度挖掘，“枝繁葉茂”。

當“種子的根”深扎于學生的頭腦，繼而“發芽、生長”，從而達到數學課堂教學的最高效，這往往就是達到了“在樹上再長片葉子而已”的效果。但長一片葉子夠不夠？能不能再多長幾片，甚至開出一朵花，結出一個果實來？當然，我們的教學不能“貪多嚼不爛”，而要尊重學生基礎，掌握教學的“度”，避免“揠苗助長”。但在允許的范圍內，我們是否可以把握時機，順水推舟，摘取幾個信手拈來的“果子”呢？我想是可以的。所以要把“種子”生長的力量盡量發揮出來，想想我的“生長課”還可以走到哪兒？即結合新舊知識間產生的新火花，思考可以解決哪些新的教學難點和學生的學困點。