學生在“說數學”中感受奇偶“美”
——《和與積的奇偶性》教學

張 婷

【教學內容】

蘇教版五年級數學下冊第50～51頁。

【教學目標】

1.使學生經歷探索利用規律解決復雜問題的結構化的教學過程，發現并理解和與積的奇偶性的規律。

2.使學生在探索規律的過程中，經歷“舉出例子——觀察比較——尋找特點——歸納規律”的方法結構，積累探索規律的相關經驗。

3.在學生經歷探索規律的結構過程中，進一步培養學生合作交流的能力和學生的語言表達能力，激發學生探究數學規律的興趣和信心，提升學生的學習能力，并能感受奇數、偶數的美。

【教學重點】

探究并發現和與積的奇偶性。

【教學難點】

理解和歸納規律。

【教學準備】

ppt、三種表格、計算器、每個學生準備一道已經算出結果的連加或連乘的算式。

【教學過程】

一、課前“敘舊”，符號記憶

師：同學們，知道我們今天學什么嗎？奇偶性的奇偶是什么意思？什么是奇數？什么是偶數？

師：明白了課題，我們就開始今天新課的學習。

二、猜想引入，引發好奇

師：今天，我們一起來探索和與積的奇偶性。（揭示課題）

1.游戲——猜想：

學生拿出課前準備的非零自然數的連加或連乘算式，學生報算式，教師迅速判斷結果是奇數還是偶數。

【設計意圖：讓學生在課的一開始迅速感知這節課的教學內容，并通過猜想游戲形式激發起學生的好奇心和好勝心，為接下來知識的學習打下良好的基礎。】

2.導語：學了今天的知識后，你也可以做到！

三、借助經驗，探索規律

（一）活動一：

1.拋出問題，激發思考。

師：我們先來研究和的奇偶性，有什么規律可尋呢？（板書：和的奇偶性）

思考一下，先從幾個數的和開始研究比較好呢？

預設：生回答：2個數、3個數、……

師：就按剛才那位同學說的，我們先來研究兩個數的和。（板書：兩個數）

從最簡單的開始想起，是一種非常重要的數學思想。

2.簡單問題，初步感受。

出示表格一：

任意選兩個不是0的自然數，求出它們的和，再看看和是奇數還是偶數。

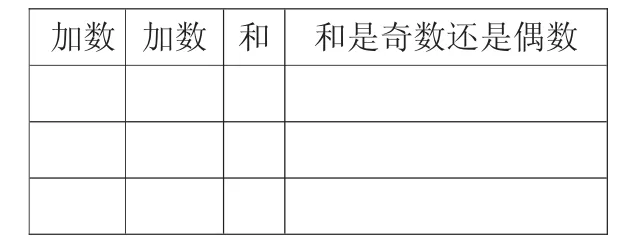
加數 加數 和 和是奇數還是偶數

活動要求：各自填表，再交流討論，寫下自己的發現。

3.深化認識，找出規律。

請學生帶著自己的表格，上臺說出發現了什么，其余同學給予評價與補充。

進一步驗證：那你們寫的算式也有這樣的規律嗎？我們來驗證一下好嗎？

誰愿意拿來給我們驗證一下，放在展臺上。

（1）這個算式符合哪個規律？這個算式呢？

（2）和是奇數，是什么樣的加數？和是偶數，是什么樣的加數？大家看看你們寫的算式符合這個規律嗎？自己驗證一下。

師：符合嗎？（符合）看來和是奇數還是偶數，與兩個加數本身是奇數還是偶數有關系。

根據學生的發現，小結并板書：

偶數+偶數=偶數

奇數+奇數=偶數

奇數+偶數=奇數

【設計意圖：讓學生通過對已有經驗的積累，自己動手操作，舉例驗證自己的發現，學生的主體地位更顯突出，鍛煉了學生的思維能力和合作能力。】

4.互動教學，及時鞏固。

互動：我來說算式，你們來判斷“和的奇偶性”好嗎？

（課件：108+2340,123459+357,1325+2608）

師：打開我們的數學書，左右兩邊頁碼的和是奇數還是偶數？你知道這是為什么嗎？

【設計意圖：使學生明白，建構一種數學規律，必須通過不斷探索，反復論證才能形成，這就是科學的態度。】

（二）活動二：

1.再拋問題，深度思考。

師：剛才研究了兩個數的和，接下來繼續研究多個數的和。（板書：多個數）

看看其中又蘊藏著怎樣的規律呢？

2.點撥問題，交流驗證。

出示表格二：

任意選幾個不是0的自然數，寫成連加算式，求出它們的和，再看看和是奇數還是偶數。

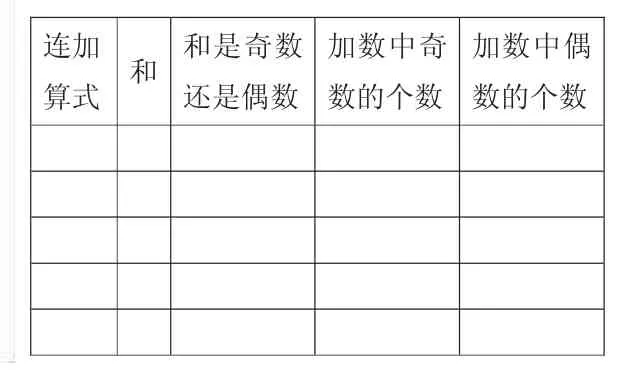
連加算式 和 和是奇數還是偶數加數中奇數的個數加數中偶數的個數

點撥：判斷和的奇偶性關鍵要看什么？為什么？

加數中奇數的個數與和的奇偶性有什么樣的關系？

活動要求：合作填表，再交流討論，寫下自己的發現。

3.匯報總結，歸納規律。

請學生帶著自己的表格，再次說出多個數相加，發現了什么。

其余同學評價補充。

師：看看你們自己的例子，有沒有不符合的？

根據學生的發現，總結并板書：

加數中奇數有奇數個，和是奇數；加數中奇數有偶數個，和是偶數。

4.解決問題，回顧反思。

（1）不計算判斷下列加法算式的和是奇數還是偶數？

25+137

2+503+17+1235

36+289+5+73+86+6759+90

（2）1+3+5+……+29你是怎么想的？

小結：和的奇偶性和誰有關啊？面對這么復雜的問題，我們從簡單的問題入手，找出規律來解決。在找規律時，可以先舉出一些例子，再通過觀察比較，找找有什么特點，從中發現規律。

（三）活動三：

師：接下來我們研究積的奇偶性。你打算先研究幾個數的積？然后呢？

【設計意圖：因有“和的奇偶性”的經驗積累，“積的奇偶性”學生便會很快發現規律，應該讓學生自然感知到思考問題的方法，活學活用。】

1.引發遷移，感受奇偶。

表格三：

要求 乘法算式 積 積是奇數還是偶數

師：請你們根據剛才的經驗，四人小組合作，舉出例子，觀察比較、尋找特點、找出規律。

2.說出想法，找出規律。

提問：哪個小組先來交流一下你們小組的結論？（學生交流）

小結并板書：

在乘法中，乘數都是奇數，積是奇數；乘數中只要有一個偶數，積就是偶數。

【設計意圖：兩個數→多個數。從簡單的問題入手，層層遞進，培養學生邏輯思維及演繹推理能力。這是重要的數學思想，也是學生解決問題的數學方法。】

四、反思質疑，歸納方法

師：本節課，我們一起學習了什么知識？剛才我們探索和發現了和與積的奇偶性的規律，回憶一下我們研究的過程，你學到了哪些解決問題的策略？

（適時板書：舉例→驗證→規律）

最后送大家一句名人名言：

把最復雜的變成最簡單的，才是最高明的。——達·芬奇

【設計意圖：這是一節“找規律”的數學活動課。學生在探索中不但要發現“和與積的奇偶性”的規律，更重要的是在發現規律的過程中感悟數學思考方法，而且還能感受到奇數、偶數獨特的“美”。】