關注知識結構發展數學思維
——計算教學中整理與復習課的教學策略

何曉紅

一、引導自主整理，提升學習能力

（一）精設問題，歸納梳理

在知識整理的過程中，教師的教學設計要多關注學生的年齡特點和認知規律，從教材中尋求依托點，精心合理地設計“整理”環節，教師拎得清，學生理得清，突出復習的重點和核心知識。如，在教學三年級上冊《萬以內的加法》和《萬以內的減法》后，筆者設計了下面的整理環節：

1.問題情境：出示“雙十一”大潤發5折活動現場圖片，提出問題。

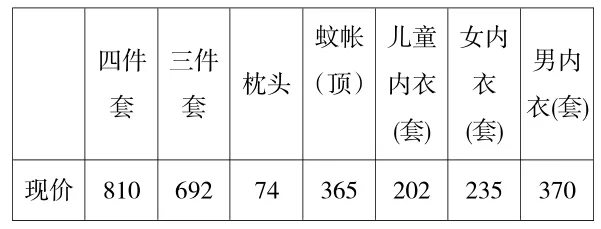
現價 810 692 74 365 202 235 370四件套三件套 枕頭蚊帳（頂）兒童內衣(套)女內衣(套)男內衣(套)

談話引入：這是“雙十一”大潤發促銷搶購現場，何老師也去了。這里有部分商品價目表，你來幫老師來算一算，同時思考：運用了本單元的哪些知識來解決問題？

（1）如果想買一個枕頭和一套兒童內衣，大約要花多少錢？（估算）

（2）如果想買男女內衣各一套，帶600元夠了嗎？（進位加法，多策略解決問題）

（3）如果帶了800元錢，買了一個三件套，還剩多少元？（退位減法）

2.反饋。（邊回答邊整理知識，形成知識結構圖）

3.思考：看上面的幾個算式，你還想到了哪些相關的知識，與同桌說一說。（設計意圖：進一步進行知識的回憶、整理、歸納，建構知識體系）

三年級的學生還沒有具備獨立自主整理單元知識、形成知識結構圖的能力。本課在具體情境中，通過幾個問題，巧妙地把這兩單元中的重、難點有機串聯，使學生在解決這些問題的同時，回憶起本單元的知識，在通過觀察幾個算式及教師的適當引導下，構建萬以內加減法的知識結構圖。

（二）巧用錯題，自主整理

在低段整理復習課中，教師應帶領學生一起回憶整理，并將一些整理方式如表格式、提綱式、圖畫式和線條式等呈現給學生。在中高段整理復習時，應逐步放手讓學生獨立自主地進行，從而促進學生自主發展。如，教學四年級下冊《運算定律整理與復習》時，筆者設計了以下環節：

1.錯題呈現（略），引導學生找出錯誤的原因。討論：如果按他這樣的計算，題目應該怎樣改？

2.學生對比分析后反饋。（有意識地進行分類）

3.回憶并記錄：這一單元我們學習了哪些運算定律?請用字母表示出來。

在《運算定律》單元中，學生最容易出現的錯誤是幾種運算定律混淆，特別是乘法分配律與乘法結合律。讓學生找出自己平時作業中的錯誤，比較貼近學生實際，更能激起學習興趣。尋找錯誤的原因，其實就是回憶計算所用到的運算定律的過程。改編題目并進行比較能更好地讓學生理解錯誤的原因、運算定律的意義，并能回顧與此相關的一些知識。再有條理地記錄整理，本單元的知識結構就清晰可見，長此以往，學生整理能力將得到大幅度的提高。

二、梳理算理算法，完善知識體系

（一）關注算法，溝通聯系

數學計算中，很多的錯誤是由于算理、算法不明或幾種算理、算法混淆。因此，復習時把分散在教材各單元中的數學計算知識概念、算理算法、定律法則，融合在一節課里，通過再一次理解、溝通、對比，把這些分散的知識點串成知識鏈，弄懂各種知識間的區別與聯系，才能從根源上提高計算的正確率。如，在五年級上冊《小數乘小數整理與復習》一課教學中，筆者設計了如下環節：

1.同時呈現三種算式（小數加減法、整數乘法、小數乘法）計算的算法，找不同。

2.出示小數加減法、整數乘法、小數乘法算理算法的推導過程圖，思考：為什么小數加減法、整數乘法時強調“相同數位對齊”，而小數乘法計算大部分時候相同數位不能對齊？為什么小數加減法時，加數（減數）中最多有幾位小數，得數也最多有幾位小數，而小數乘法計算時，因數中一共有幾位小數，積中就有幾位小數？

3.出示三種計算，聯系生活實際，編一個解決問題，并計算。（通過解決問題，再一次溝通、對比三種計算的算理算法）

在本單元中，出現比較多的錯誤是：把小數乘法與小數加減法算法混為一談，又受“按整數乘法進行計算”的負遷移。因此，復習時把小數加減法、整數乘法、小數乘法的算理、算法進行梳理、溝通、比較，顯得尤為重要。

（二）靈活運用，綜合拓展

在計算復習的教學中，要針對整理的知識精心設計學生的自主練習，使學生能靈活運用所整理、復習的知識去解決相關問題，并通過練習對相關知識進行適當擴展，便于下一階段更好地進行知識梳理與新知學習。如，三上《萬以內的加、減法整理復習》一課教學時，筆者設計了以下練習環節：

談話過渡：根據這些數據還可以提很多的問題，列很多的算式，為了方便，請你按要求編一編算式。

1．選兩個數，按要求編算 式 ：810、692、74、365、202、235、370。

（1）不進位加法。（2）進位加法。（3）不退位減法。（4）退位減法。（5）得數最大。（6）得數接近300。

要求：（1）觀察數據，選擇兩個數編一編。（2）編好后，判斷是否符合要求。（3）選擇其中一部分計算。

2.學生獨立完成，教師巡視，批一批。選擇一個正確的和幾個錯誤的進行反饋，說說是怎么編的。

3.呈現正確答案，請學生來說一說，是怎么編的。（預設：每個數位相加不滿十，至少有一個數位相加滿十，每個數位相減都夠了，至少有一個數位相減是不夠的，選最大的兩個數，加減后得數接近300的）

在前一環節整理之后，不急著做題，而是讓學生根據要求再編一編，不僅能使學生繼續保持良好的學習興趣，還以編題這一線索，把兩單元知識整合起來，能有效地理清進位與否、退位與否、估算、精算等知識間的聯系與區別，更能靈活地運用兩單元的知識解決問題，為知識的拓展與延伸創設了空間，可謂一舉多得。

三、點面互通融合，凸顯數學思想

（一）遷移類推，融會貫通

在計算教學的整理與復習課中，為使學生獲得穩定、清晰的數學概念，可以聯系學生的生活實際，根據需要聯系各學科對相關知識進行適當擴展，并鼓勵學生在解決問題時策略的多樣化，重在培養學生應用數學的意識和能力。如，在六年級下冊《比與比例》單元的學習、整理復習之后，筆者設計了如下課外拓展題：

1.出示杠桿，說說與比例有什么關系？

2.如果只用尺子和這個杠桿，你能測量出這塊石頭的重量嗎？（如果有困難，可以找老師要錦囊妙計）

一石激起千層浪，學生有的開始畫杠桿，有的找同桌商量，顯得熱情高漲。測量石頭的重量與杠桿有什么關系？課外學生查找復習了杠桿知識，明白了：杠桿原理就是運用了比例的知識，是反比例的運用。生活中所用的測量物體質量的秤都是利用杠桿原理制作而成的，所以運用反比例的知識，就可以只用尺子，測量出石頭的重量。

（二）梯度推進，彰顯思維

知識的習得、能力的培養一般要經歷模仿、熟練、創造三個階段。因此，相應的練習設計也要由易到難，分層次、有梯度，才能滿足各層次學生的學習需求，每一名學生都能激發出求知的欲望，以及收獲學習成功的喜悅。在復習課中合理地設計練習的數量和梯度是很有必要的，且要注意“精”和“準”。如，在三年級上冊《萬以內加減法的整理與復習》的教學中，筆者設計了如下拓展題：

填一填：（1）□73+335（6、7、8、9）方框填哪些數，使它成為連續進位的加法？

3□0-265（6、5、4、3、2、1、0）方框里填哪些數，使它成為連續退位減法？

（2）把算式填完整。

在練習環節，針對重難點、易錯題，多角度、多形式、分層次的設計，既能讓每一位學生在多樣的練習中獲得數學上的收獲，又能讓他們在有效的練習中獲得數學思想，發展數學思維。