中職數學概念教學例談

[摘要]數學概念是整個數學知識體系中最核心的部分，學生只有學好數學概念，才能進行正確地判斷、推理和證明。中職數學教師要認真分析數學概念教學中存在的問題，根據中職學生的認知特點和學習能力，做好數學概念的引入，講清數學概念的本質和內涵，強化數學概念的應用，培養學生能力，發展學生智力。

[關鍵詞]中職數學；概念教學；教學方法

[中圖分類號]G712 [文獻標志碼]A [文章編號]1005-6009（2016）14-0055-02

[作者簡介]趙林，江蘇省句容中等專業學校（江蘇鎮江，212400）高級教師，鎮江市中青年骨干教師，主要研究方向為中職數學教學。

數學概念是人腦對客觀現實中數量關系和空間形式本質特征的一種反映，是學生學習一切數學知識的基礎。如果數學概念不清，學生就會思路閉塞、邏輯混亂，即使是一些教師反復強調過的簡單的知識點在考試中也會反復犯錯。分析試卷后發現，錯誤主要原因還是學生對數學概念的理解不夠透徹，對數學概念的應用和轉化不靈活。因此，中職數學教師不能只重視典型例題的講解和解題技巧的訓練，更應強調數學概念的教學。筆者結合自己多年的教學實踐，對中職數學概念教學談幾點粗淺的看法。

一、中職數學概念教學存在的問題

受傳統教學觀念的影響，很多中職數學教師認為數學教學就是教給學生解題的方法，因此把課堂上的大部分時間花在解題技巧的訓練上，對數學概念教學則一帶而過。學生對概念的認識僅僅停留在表面，沒有從本質上理解概念的內涵。中職學生和普高學生相比，無論是數學基礎，還是理解能力都有一定的差距，如果教師沒有講清、講透數學概念表述中的關鍵詞和注意點，學生不能形成正確的概念，也就把握不住概念的本質特征。所以當他們遇到沒見過的題型或者題目要求稍一變化時，就會束手無策，錯誤百出。

二、中職數學概念教學的方法

（一）用直觀形象的方法引入概念

對于解析幾何和立體幾何中有些概念，我們可以通過直觀形象的數學教具或模型來引入，幫助學生理解和掌握。例如，在講授橢圓的概念時，教師可布置學生在課前每人準備一張硬紙板，一條細線繩，兩個圖釘。上課時要求學生將兩個圖釘固定在硬紙板上，并且繩子的長度要大于兩個圖釘之間的距離，然后再用鉛筆將繩子拉緊開始畫線，最后畫出的曲線就是橢圓。這樣就形象直觀地顯示了橢圓的本質屬性，即“平面內到兩個定點的距離之和等于定長的點的軌跡就是橢圓”。

（二）用數形結合的思想講解概念

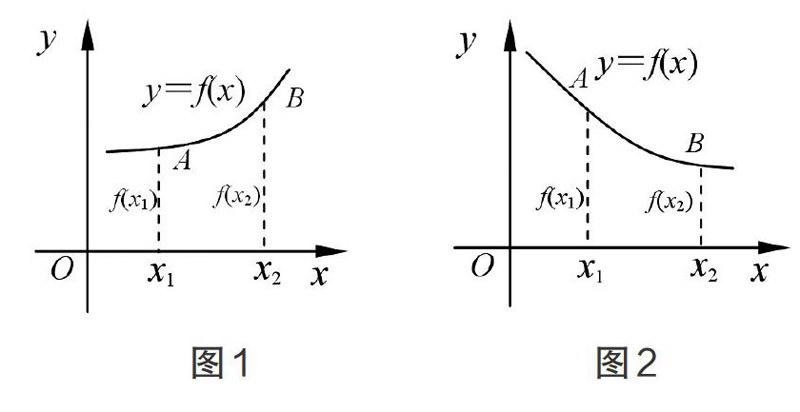
數形結合思想在數學教學中非常重要，有些數學概念單靠文字來表達，學生難以捉摸。如果我們采用數形結合的方法，把枯燥的文字描述轉化為圖形來表示，那么就顯得具體形象得多。例如，函數單調性的概念是：對屬于定義域D內某個區間上任意兩個自變量的值x1、x2，當x1f（x2），那么就說f（x）在區間D上是減函數，增函數和減函數統稱為單調函數。由于該定義文字較長又有數學符號，學生比較難理解。如果我們畫出圖形，引導學生從左往右觀察，若圖像上升就是增函數（如圖1），圖像下降就是減函數（如圖2），這樣學生不但容易理解，而且記憶深刻。

（三）用準確無誤的語言描述概念

教師的教學語言不但要生動有趣，而且還要準確無誤。尤其在數學概念教學中，教師更要講清關鍵的字句，這樣學生才能深刻理解。例如，映射的概念是：“一般地，設A、B是兩個非空集合，如果按照某種對應法則廠對于A中的任意一個元素，在B中都有唯一確定的元素和它對應，那么這樣的對應法則廠就叫做集合A到集合B的映射。”教師在講映射這一概念時，要特別強調“任意、都有、唯一”這幾個關鍵詞。如果不注意概念中的約束條件，縮小了概念的內涵，就擴大了概念的外延，學生對數學概念的理解就會出現偏差。

（四）用聯系對比的方法區別概念

教師在課堂教學中應將一些容易混淆的數學概念放到一起作對比，讓學生掌握它們之間的共同點和不同點，并能做出正確的判斷和選擇。例如，排列和組合這兩個概念，學生在解題時經常出現錯誤，因此，教師可通過舉例來說明。從10名同學中選出2人，問：1.分別擔任正、副班長有多少種不同的選法？2.去參加學校座談會有多少種不同的選法？這兩個問題的共同之處是都要選出2人。不同之處是，問題1中選2人擔任正、副班長是有順序性的，因此屬于排列問題；而問題2中選2人去開會是沒有順序性的，那就是組合問題。再如，不少學生對概率中的互斥事件與對立事件分不清。實際上互斥事件與對立事件都是對兩個事件而言的，它們之間既有聯系又有區別。在一次實驗中，兩個互斥的事件有可能都不發生，也可能有一個發生，但不能同時發生；而兩個對立的事件則必有一個發生，也不能同時發生。所以兩個事件互斥，它們未必對立；反之，兩個事件對立，它們一定互斥。

（五）用變式變形的方式完善概念

變式是一種重要的數學教學方法，通過變式可以讓學生把問題看得更清楚、更透徹，有些數學概念就可以采用變式教學，使學生更好地掌握這些概念的本質屬性。例如，等差中項的概念，書上是這樣敘述的：如果a、b、c三個數成等差數列，那么6就叫作。和c的等差中項。除了知道這一文字描述外，還必須認識變式：a-b=b-c、26=s+c、b=（a+c）/2，這些結論都是等價的，這樣學生在解題時，才能靈活運用。

變形是幾何教學中常用的方法，通過圖形變換，可以使學生對幾何中有些概念理解得更準確。例如，四棱柱的分類較多，學生不易弄清楚，我們可以通過圖形變換幫助學生理解，當四棱柱側棱與底面垂直時就變成了直四棱柱，當直四棱柱底面為長方形時就變成了長方體，當長方體底面為正方形時就變成了正四棱柱，當正四棱柱的側棱和底面邊長相等時就變成了正方體。這樣學生就掌握了直四棱柱、長方體、正四棱柱、正方體的概念及它們之間的關系。

（六）用變化發展的觀點深化概念

雖然每個數學概念都有它確定的含義，但隨著科學技術的發展和數學知識的不斷豐富，有的數學概念也在發生著變化。例如，平方根在初中教材上是這樣敘述的：如果一個數的平方等于a，那么這個數就叫作a的平方根。一個正數有兩個平方根，它們互為相反數；0的平方根還是0；負數沒有平方根。但隨著數系的擴充，到高中學習了復數之后，負數也可以開平方根了，它們是一對共軛純虛數。

概念教學貫穿于整個數學教學的過程，能否把數學概念講好，直接影響著課堂的教學效果。雖然中職數學的教學現狀不容樂觀，學生學好數學也有一定的難度，但教師只要認真鉆研數學教材，采取行之有效的教學方法，相信一定能把數學概念教好，也一定能提高中職數學的教學質量。