基于動態罰因子的多學科協同優化算法及其在船舶設計中的應用

周 奇，蔣 平，許 輝，陳 立，黃衛剛

（1.華中科技大學機械學院，武漢430074；2.中國艦船研究設計中心，武漢430064）

基于動態罰因子的多學科協同優化算法及其在船舶設計中的應用

周 奇1，2，蔣 平1，許 輝2，陳 立2，黃衛剛2

（1.華中科技大學機械學院，武漢430074；2.中國艦船研究設計中心，武漢430064）

針對標準協同優化算法求解復雜系統工程問題的缺陷，提出了一種改進的協同優化算法，并將其應用于油船總體概念設計階段。改進協同優化算法將系統級一致性約束最優化問題通過罰函數方法轉化為一個無約束優化問題。同時，給出了兩種不同的基于差異信息的動態可調罰系數，以保證在優化初期，系統級設計變量與學科級共享變量相差較大時，懲罰力度也大，促使一致性差異在總目標函數中占主導地位，則一致性差異將迅速下降。隨著優化的進行，罰系數變小，懲罰力度減輕，目標函數的收斂加快。通過對MDO測試函數算例與標準協同優化和其他典型的改進協同算法的比較，驗證了該方法在優化結果的可靠性和穩定性等方面有優勢。最后，應用改進的協同優化算法求解以油船造價為系統級目標協同浮性與穩性、快速性等4個子學科的多學科優化問題以體現其工程實用性。

多學科設計；協同優化；罰系數；差異信息；船舶概念設計

0 引 言

現代工程設計往往涉及多個專業領域，存在很多設計變量及約束條件，各學科間相互影響或耦合。傳統的串行設計方式由于忽視學科間的關聯性，通常只能獲得設計的局部最優解。上世紀八十年代，興起于航空航天領域的多學科設計優化方法（Multidisciplinary Design Optimization，簡稱MDO）成為解決復雜耦合系統優化設計的可行方法之一。

MDO是一種通過充分探索和利用工程系統中相互作用的協同機制來設計復雜產品及其子系統的方法論[1]。以Sobieski和Kroo為代表的科學家在這方面做了一些開創性的工作[2-3]。隨后，MDO在航天航空實際工程應用過程中得到了廣泛的發展。MDO在船舶領域的應用研究起步較晚，最負盛名的是美國DD-21項目在概念設計階段應用多學科設計優化技術進行新武器系統實際開發，并從2004年開始并行地進行全面的詳細設計與生產，2009年完成32艘DD-21級艦只交付組艦艦隊任務；2007年Shinde在California大學和商用運輸技術中心（Center for the Commercial Deployment Of Transportation Technologies，簡稱CCDOTT）的支持下完成了輕型高速海上運輸船（Joint High Speed Sea Lift Light,簡稱HSS Light）、高速海上運輸船（High Speed Sea Lift,簡稱HSS）、高速運輸連接船（High Speed Connector Ship,簡稱HSC）三型三體船的多學科概念優化設計，隨后California大學的Rispin、Hefazi等[4]在此基礎上進行了進一步的研究；Seoul National大學的Yang[5]在船舶初步設計階段，考慮船體型線設計，完成VLCC多學科優化設計；Michigan大學的Christopher[6]將粒子群算法與協同優化算法結合，以年運貨量、單位重量運輸費用、空船質量為優化目標完成了雜貨船多學科概念設計。

國內船舶多學科優化的研究暫處于理論研究階段。中國船舶科學研究中心趙峰等[7]分析了水面艦船航行性能設計領域開展多學科設計優化的重要意義，制定了船舶總體研究思路，確定了系統設計目標、技術指標及頂層設計方案，剖析了需要解決的關鍵技術，并給出了攻關建議；潘彬彬等[8-9]建立了整船的有限元模型，完成了整船結構多學科設計優化，同時在中國船舶科學研究中心的支持下，對國內的一艘實船的概念設計建立了包括快速性、操縱性和船中剖面的總縱強度多學科設計優化模型，最終的優化設計方案不僅提高了該船的快速性，同時減小了船中剖面的截面積；上海交通大學胡志強等[10]在8000箱集裝箱船的緩沖球鼻艏設計中采用多學科協同優化算法，獲得了滿足船東利益和船級社規范要求的優化解；劉蔚等[11-12]將多學科設計優化方法應用到7000米載人潛水器的總體設計過程中，建立了比較完整的數學模型，與原設計方案相比，找到了進一步改進設計的空間，同時在單學科可行方向法（Individual Discipline Feasible，簡稱IDF）的基礎上提出兩層分級框架（Bi-Level Hierarchic，簡稱BLH），將其應用于自治水下潛水器（Autonomous Underwater Vehicle，簡稱AUV）的總體設計；趙敏等[13]采用兩級集成系統協同優化（Bi-Level Integrated System Collaborative Optimization，簡稱BLISCO）對載人潛水器（Human Occupied Vehicle，簡稱HOV）進行了總體概念設計；武漢理工大學馮佰威等[14]概述了艦船多學科綜合優化設計計算環境特征，進而對船體型線多學科優化進行深入的研究。

作為多學科設計優化研究領域的核心，MDO算法旨在提出有效的設計計算框架，將復雜的工程問題解耦以減輕MDO的計算復雜性與組織復雜性，進而實現并行優化設計。隨著MDO的發展，涌現出諸如多學科可行方向法（Multidisciplinary Feasible Method，簡稱MDF）、并行子空間優化算法（Concurrent Subspace Optimization，簡稱CSSO）、協同優化算法（Collaborate Optimization，簡稱CO）、兩級集成系統綜合（Bi-level Integrated System Synthesis，簡稱BLISS）等優化策略。其中1994年斯坦福大學教授Kroo等[2]提出的協同優化算法由于具有良好的學科自治性和并行處理能力，一直被認為是多學科優化中最具前途的優化算法，吸引了國內外不少學者將其應用于火箭、衛星、電動汽車、魚雷、渦輪機及船體結構的設計[15-22]。

雖然CO在工程應用領域得到了廣泛的應用，但CO的收斂性并沒有得到嚴格的數學證明。同時，在實際運用過程中CO表現出計算方面的困難。NASA在對IDF、MDF、及CO的收斂性能進行測試與評估的過程中，發現CO對于解決齒輪減速箱、電器封裝、丙烷燃燒等十大測試實例存在計算成本大、對初始點敏感甚至無法收斂等缺陷[23]。針對CO方法的不足，國內外學者在繼承CO兩級優化框架的基礎上致力于提高CO的數值穩定性。研究工作主要包含三個方面：一是采用近似技術建立系統級約束的代理模型來降低計算成本和光滑數值噪聲。如響應面近似模型[24]、徑向基神經網絡模型[25]、Kriging模型[26]；二是采用具有優秀全局搜索能力的現代智能算法，如遺傳算法[27]和粒子群算法[6]取代系統級中基于梯度的優化算法。三是采用松弛因子[28-29]，將系統級一致性等式約束變換為不等式約束，以降低優化迭代難度，提高總體收斂效率。

本文從幾何角度分析了系統級優化迭代過程，提出了一種基于一致性差異信息的動態罰函數協同優化算法（Dynamic Penalty Collaborative Optimization,簡稱DPCO），并應用經典的MDO測試函數驗證了其有效性。最后，將其應用于35000DWT原油船航行性能多學科優化以體現其工程實用性。

1 多學科協同優化算法

1.1 協同優化算法的數學描述及求解流程

協同優化算法是1994年斯坦福大學教授Kroo等針對單級優化方法在解決大型復雜系統工程時出現的低效率和大計算量問題，提出來的具有兩級結構的多學科優化策略。CO將優化問題分為兩級：一個系統級和并行的多個學科級。系統級的數學描述形式如下：

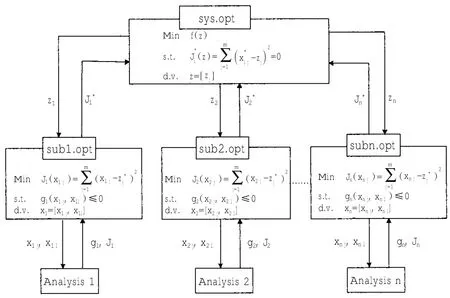
圖1 標準CO流程Fig.1 Flow chart of traditional CO

1.2 協同優化計算困難的原因

協同優化算法中系統級獨特的一致性等式約束條件形式被認為是造成其收斂缺陷的直接原因[29]。具體分析如下：

（1）在最優解處，系統級解域不光滑。

Fiacco和McCormick認為非線性規劃最優解域光滑的非退化條件是一階充分條件、線性獨立約束條件和嚴格互補性條件。CO系統級L-2范數嚴格一致性等式約束在最優解處不可導，無法滿足非退化條件，基于梯度的優化方法無法保證解的收斂性。

（2）系統級約束在最優處矩陣為奇異矩陣，導致系統級優化的Kuhn-Tucker條件無法滿足。

系統級Kuhn-Tucker為：

（3）對于實際的復雜MDO問題，子學科數目往往多于系統級共享變量數目，使得系統級約束條件數大于系統級共享變量數，極大地限制了系統級優化的自由度。同時，系統級一致性約束與系統級目標直接關聯性不強，難以確定系統級的有效集。

2 改進的協同優化算法

2.1 改進協同優化算法的結構

前文分析了造成CO優化困難的主要原因是其系統級一致性約束表述，如果能夠將系統級一致性約束最優化問題轉化為一個無約束優化問題，則系統級優化將不存在上述計算困難，這將是非常有利的。本文的方法正是基于這種設想提出來的。它的思路是：在原系統級優化問題的目標函數中，引入某些反映約束影響的附加項，構成一個新的無約束最優化問題的目標函數，通過合理選擇附加項，可以使這個新目標函數的無約束最優點序列收斂到原問題的最優點。

原系統級優化問題為：

現轉化為下述無約束優化問題：

式中：f（ z）為原設計問題的目標函數；s為在目標函數和約束影響項之間起加權作用的參數，稱為罰系數；λ為懲罰放大因子；為一致性約束條件。由上式可知，當探求點zk位于非可行區域時，即約束條件不滿足時，s取值越大，f（ z,s）就越大，因此對于不滿足約束是一種“懲罰”。反之，當探求點zk位于可行區域時，不論s取何值，附加項均為0，f（ z,s）取得與f（ z）相當的值，也就是說約束條件滿足時不受“懲罰”。

系統級一致性約束的目的即是滿足一致性約束條件下系統級目標最優，因此合理選取罰系數，對優化收斂性能起決定性的作用。罰系數取值過大，一致性約束在總的目標函數中占有比重較大，一致性較易得到滿足，但目標函數減少緩慢；反之，罰系數取值過小，原目標函數在總的目標函數中占有比重上升，目標函數迅速減少，但“懲罰”作用不明顯易導致一致性差異過大。所以，固定的罰系數不適合此問題的求解。本文基于系統級迭代過程的幾何分析，給出了兩種不同的基于差異信息的動態可調罰系數。

（1）學科設計點之間的差異性：

以兩學科一維設計問題為例，系統級在第k次迭代所得優化解為zk，并將zk傳遞給學科1和學科2，學科級的優化目標為學科級設計變量與zk的距離最短，則必位于gi之上，且滿足與gi在處的切線垂直。如圖2所示，用r為半徑的圓表示下一個系統級優化設計點zk+1與學科級間的允許最大差異性范圍。兩圓相交部分即為系統級可行解域。隨著優化過程的進行，r逐漸變小，直至重合。若定義，i=1,2,…n，j=1,2,…n，則優化整個過程中，s總能動態反應一致性差異信息。

（2）系統級與學科設計點之間的差異性：

同樣以兩學科一維設計問題為例，圖3所示為第k次迭代所得優化解為zk與學科級的差異示意圖。隨著優化迭代的進行不斷向zk靠攏直至重合，即若定義s=max（ xi-z）2，i=1,2,…n，則優化整個過程中，s總能動態反應一致性差異信息。

通過上述兩種一致性差異信息s構造罰系數能保證系統級目標函數逐步逼近最優解。在優化初期，系統級設計變量與學科級共享變量相差較大，即一致性差異過大時，懲罰力度也大，一致性差異在總目標函數中占主導地位，促使一致性差異將迅速下降，隨著優化的進行，罰系數下降，懲罰力度減輕，目標函數的收斂加快。

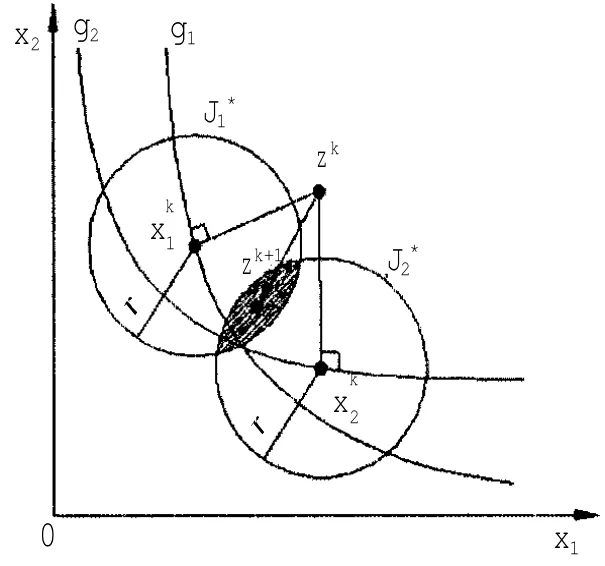
圖2 學科間一致性差異的幾何示意Fig.2 Geometrical description of discrepancy information between disciplines

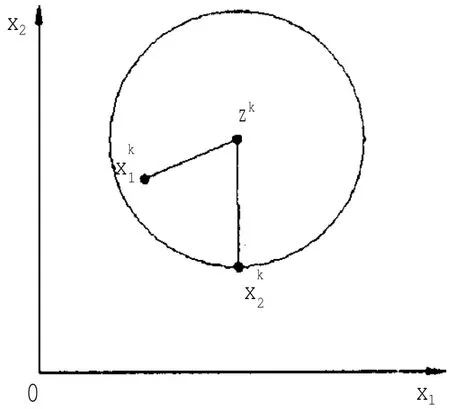
圖3 系統級與學科間一致性差異的幾何示意Fig.3 Geometrical description of discrepancy information between system and disciplines

2.2 算例分析

典型函數優化問題，其數學模型為[30]：

按照協同優化的思想，將該優化問題分為一個系統級和兩個學科級。協同優化算法的系統級數學優化模型如下：

式中：z1，z2為系統級設計變量為系統級一致性約束。

（2）子學科1的優化模型：

（3）子學科2的優化模型：

采用DPCO算法對系統級表述形式進行改進，改進后的系統級優化模型：

子系統級優化數學模型表述不變。

由文獻[30]可知，當β=0.1時，優化問題的理論最優解x*為（0.198，1.980），目標函數f*為3.960。為檢驗本文方法的收斂性，取三組不同初始點，選取標準CO、文獻[29]提出的松弛CO和文獻[31]改進的CO進行比較研究。四種優化方法系統級和子系統級都采用序列二次規劃法（NLPQL），優化結果如表1所示。

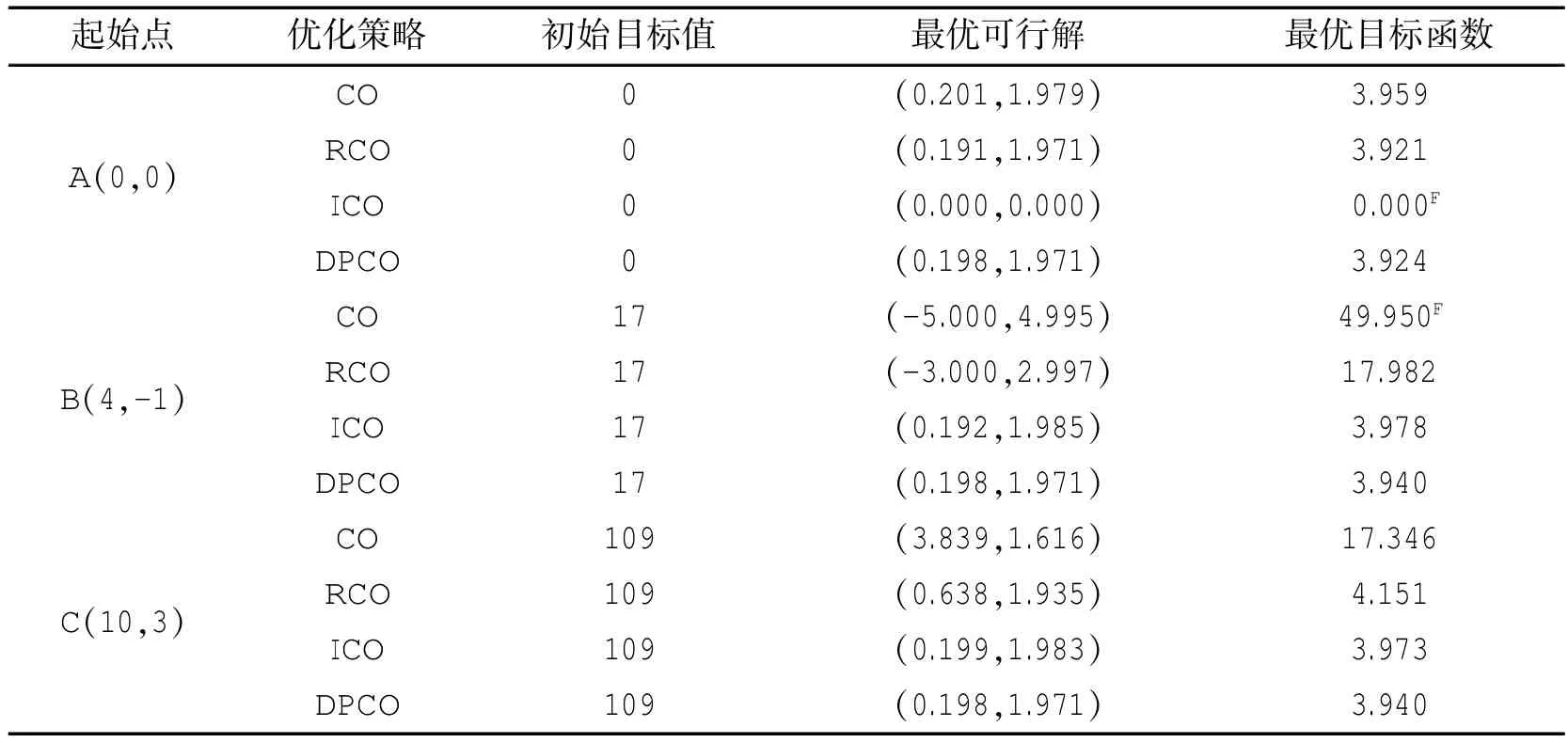
表1 優化結果比較Tab.1 Comparison of the optimization results

由表1可以看出，針對3個不同的初始點，DPCO總能收斂至理論最優解附近，即收斂魯棒性較好。其他三種方法在優化迭代過程中存在一定的計算困難，難以確保優化結果收斂。

3 船舶航行性能多學科協同優化模型與求解

本文討論一艘載重量35000DWT油船，主機選用一臺MAN6S42MC7，常用功率5 076 kW/110 r/min，球艏中心至龍骨高度hb=4 m，附體濕表面積SAPP=50 m2，球艏橫截面積ABT=20 m2，船艉橫截面積AT=16 m2，海水溫度15°，采用AU型4葉螺旋槳，單槳，敞水式尾部，矩形舵板。

3.1 學科分析

根據總體概念設計流程，按照多學科協同優化設計思路，將散貨船概念設計分為以船舶造價為系統控制層協調浮性與穩性、艙容性、快速性（阻力和推進）和操縱性四個子學科級，如圖4所示。

多學科協同優化具體描述如下：

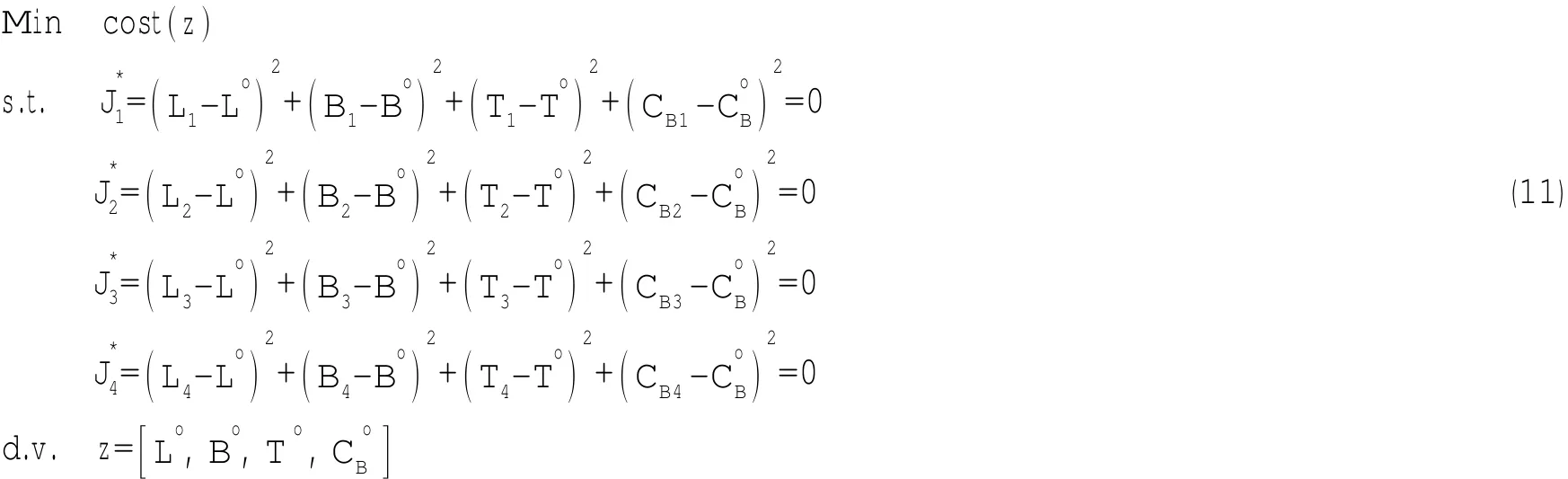
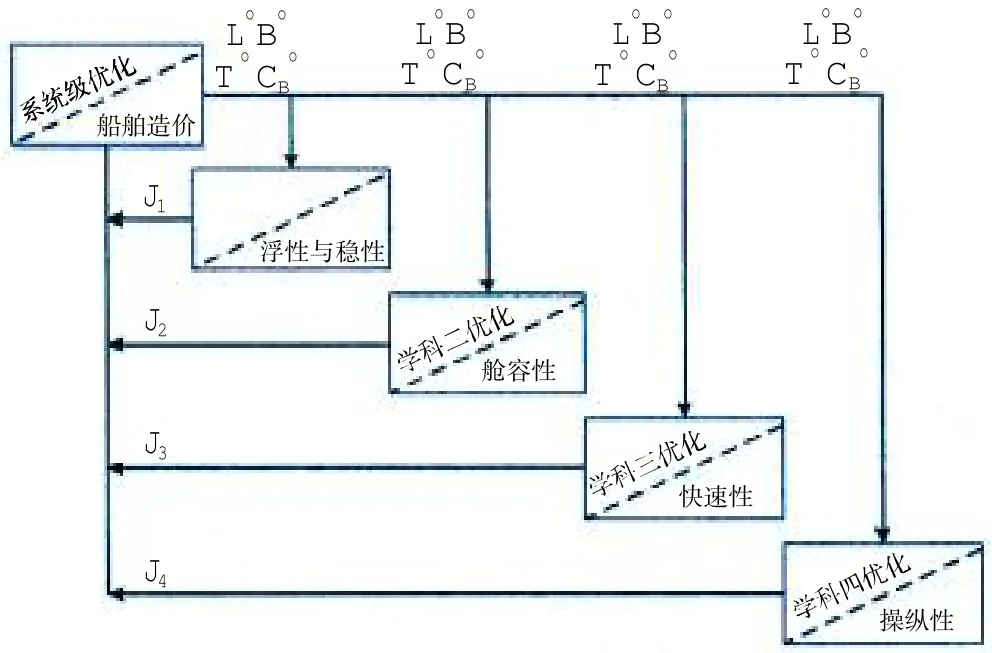
圖4 船舶概念設計多學科協同優化結構框架Fig.4 Frame of conceptual design of ship in CO

（1）系統級優化問題：其中船舶造價采用分項估價法，將船舶分成船體鋼料Ws、舾裝設備Wo和機電設備Wm三大項。分項的價格均根據其重量乘以每噸價格估算。由此可以寫出船價估算公式：

式中：rs，ro，rm為船體鋼料，舾裝，機電設備每噸的價格。本文取rs=0.5萬元/t，ro=0.8萬元/t，rm=1.5萬元/t。（2）學科1浮性與穩性子學科優化問題：式中第一個約束表示重量W和排水量Δ相等，考慮船舶初步設計階段誤差，在實際優化過程中，控制兩者的相對誤差ε在5%以內。即其中W由空船重量W和載重量DWT兩個部分組

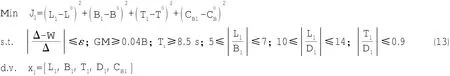
L成，空船重量WL按照船體鋼料Ws、舾裝設備Wo和機電設備Wm計算：a.船體鋼料的重量估算

b.舾裝重量估算

c.機電設備重量估算

式中：P為主機額定功率（kW）。

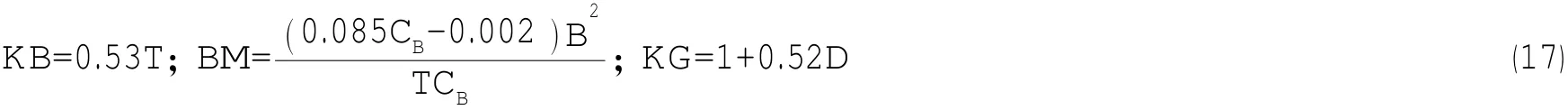
（3）學科2艙容性子學科優化問題：

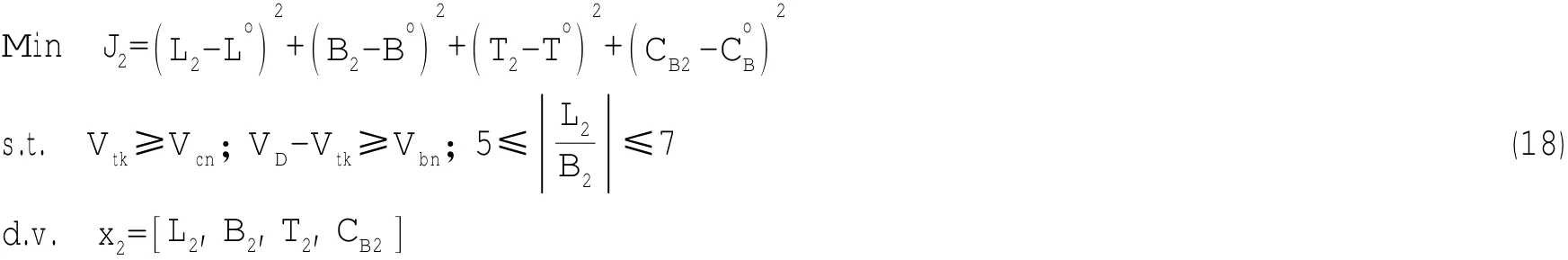
式中：Vtk為貨油艙能提供的容積（m3）；VD為貨油區能提供的總容積（m3）；Vcn為貨油所需容積（m3）；Vbn為壓載艙所需容積（m3）。其中大型油船壓載水艙容積Vbn為30%DW-40%DW。

（4）學科3快速性子學科優化問題：

式中第一個約束為螺旋槳推力平衡約束，其中RT為船舶總阻力，采用Holtrop阻力公式估算[32]：

n為轉速；t為推力減額分數，對于單槳船，采用霍爾特洛潑公式：

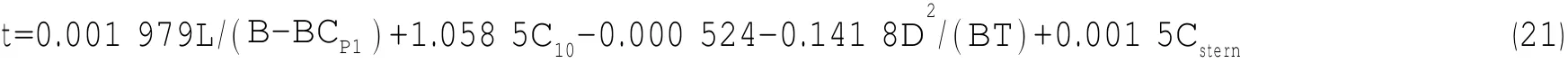
KT為推力系數，采用上海交通大學AU型螺旋槳經驗回歸公式[32]

第二個約束為螺旋槳轉矩平衡約束，約束中的KQ為扭矩系數。采用上海交通大學AU型螺旋槳經驗回歸公式[33]：

在實際優化過程中將上述兩個等式約束同重力浮力等式一樣做松弛處理。

第三個約束為螺旋槳空泡約束條件。對于單槳船，K=0.2，Tp為螺旋槳推力，Tp=RT/（1-t）。Z為螺旋槳槳葉數。po+ρgh為槳軸線處靜水壓力。pv為水的汽化壓力。

（5）學科4操縱性子學科優化問題：

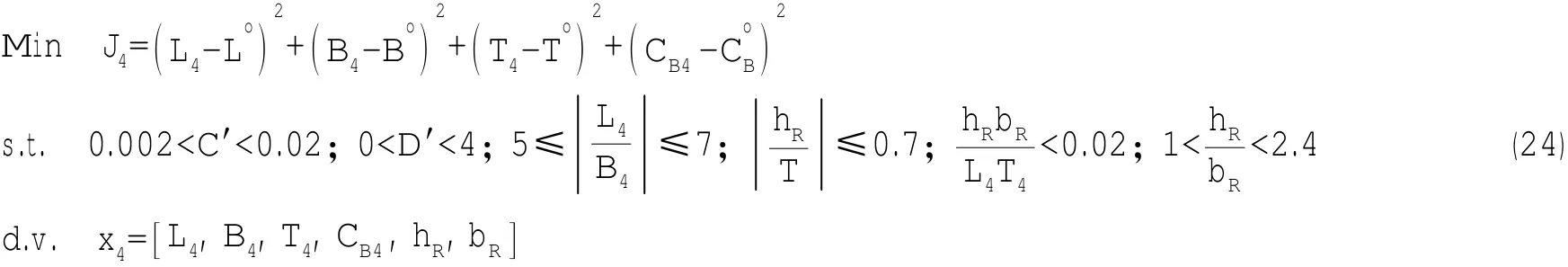
約束式中第一個約束中C′為直線穩定性衡準數。由下式計算：

式中：Nv′、Nr′、Yv′、Yr′為無因次力矩系數和水動力系數；m′和λ11′為船體質量和附加質量的無因次系數。

附加質量系數采用回歸公式：

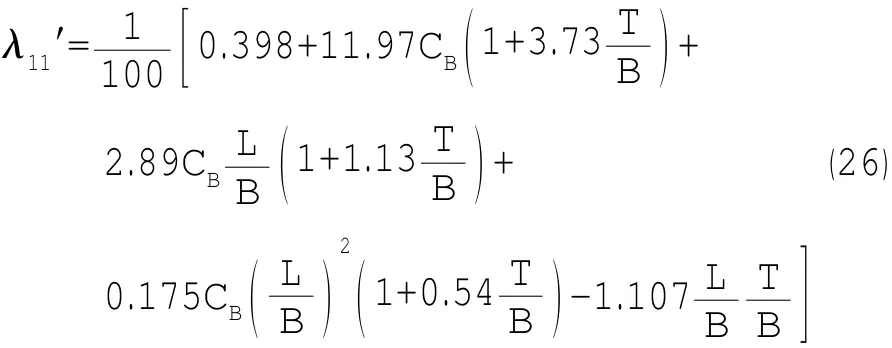
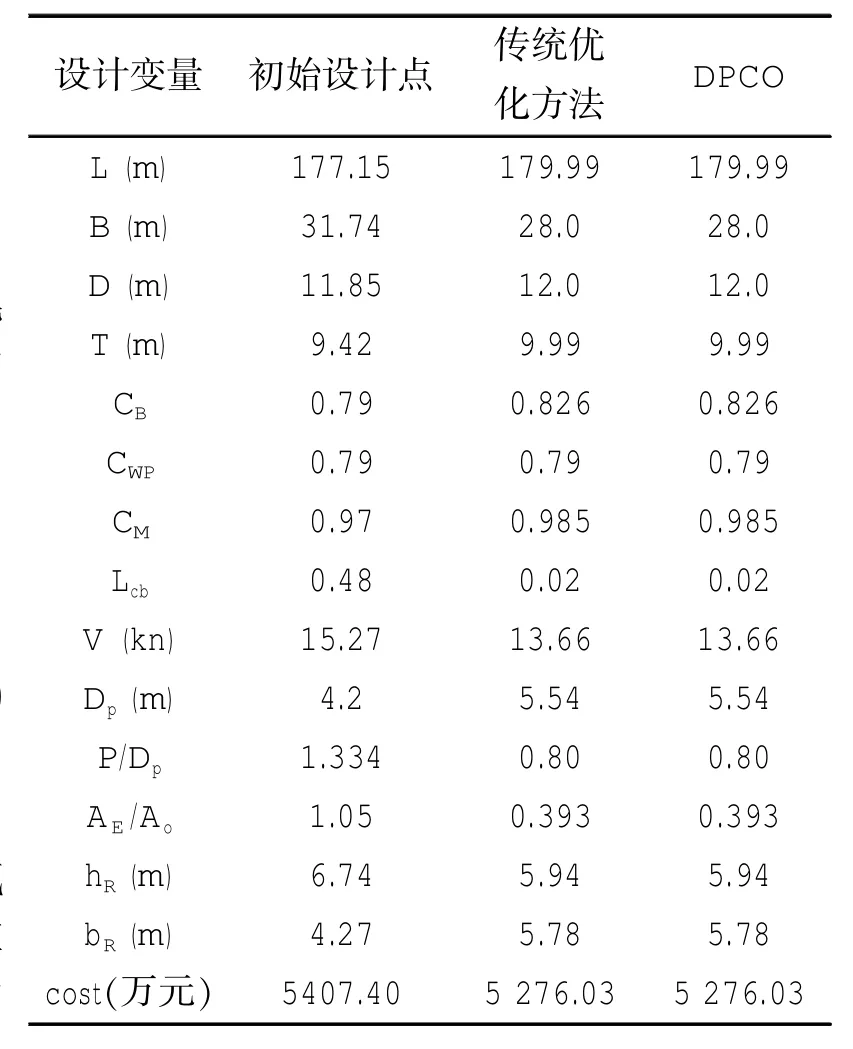
表2 設計變量及目標優化結果Tab.2 Results of optimum

第二個約束中D′為相對回轉直徑，對于敞水式尾部，相對回轉直徑的計算采用Lyster和Knights的回歸公式[34]：

式中：δ為舵角，Ab為艏部浸濕面積，Trim為船舶縱傾。

3.2 優化結果分析

為了驗證本方法的有效性，對全系統采用整體集成的單學科優化思路求解，優化算法采用序列二次優化算法，優化結果列于表4中。傳統CO因協同失敗而未列出優化結果。由對比結果可以看出，DPCO與傳統優化方法所求得結果基本一致，表明本文方法適用于船舶性能綜合優化問題。

4 結 論

（1）協同優化算法作為多學科優化設計優化中應用最廣泛的求解策略，針對標準協同優化算法的不足，通過引入兩種能反映學科與系統級間差異信息的動態因子，將系統級有約束優化問題轉化為無約束動態懲罰數優化，通過兩個經典測試算例驗證了該方法能有效改善標準協同優化的優化性能。

（2）以油船總體性能優化設計為例，綜合考慮船舶航行性能和經濟建造性之間的耦合關系，建立概念設計階段的多學科協同優化框架。以改進的協同優化方法為求解策略，有效地避免了傳統協同優化在求解此復雜系統優化問題無法收斂的缺陷，得到了穩定、可靠的優化解，對處理船舶多學科優化問題并行計算和分工協作提供了有價值的解決方法。

（3）在實際工程運用中，學科分析可以引入各類先進的數值仿真軟件來提高設計精度。然后，利用近似技術（響應面近似技術、Kriging模型和徑向基函數模型）將高精度分析結果引入到多學科優化過程中進行迭代分析，這樣可以獲得更加合理準確的設計方法。

[1]Sobieszczanski-Sobieski J,Haftka R T.Multidisciplinary aerospace design optimization:survey of recent developments[J]. Structural and Multidisciplinary Optimization,1997,14(1):1-23.

[2]Kroo I,Altus S,Braun R,et al.Multidisciplinary optimization methods for aircraft preliminary design[J].AIAA paper, 1994,4325.

[3]Sobieszczanski-Sobieski J.Multidisciplinary design optimization-An emerging new engineering discipline[C]//World Congress on Optimal Design of Structural Systems.Rio de Janeiro,Brazil,1993:1993.

[4]Hefazi H,Mizine I,Schmitz A,et al.Multidisciplinary synthesis optimization process in multihull ship design[J].Naval Engineers Journal,2010,122(3):29-47.

[5]Yang Y S,Park C K,Lee K H,et al.A study on the preliminary ship design method using deterministic approach and probabilistic approach including hull form[J].Structural and Multidisciplinary Optimization,2007,33(6):529-539.

[6]Hart C G,Vlahopoulos N.An integrated multidisciplinary particle swarm optimization approach to conceptual ship design [J].Structural and Multidisciplinary Optimization,2010,41(3):481-494.

[7]趙 峰,程素斌,楊 磊,等.水面艦船航行性能MDO系統頂層設計研究[J].船舶力學,2012,16(11):1257-1266. Zhao Feng,Cheng Subin,Yang Lei,et al.Top-down design research for the navigational performance MDO system of naval surface combatant[J].Journal of Ship Mechanics,2012,16(11):1257-1266.

[8]潘彬彬,崔維成.基于有限元的整船結構多學科設計優化[J].中國造船,2010,51(1):47-54. Pan Binbin,Cui Weicheng.FEM based MEDO model for entire ship structural optimization[J].Shipbuilding of China,2010, 51(1):47-54.

[9]Pan Binbin,Cui Weicheng,He Lin.A ship hull transform program for multidisciplinary design optimization[J].Journal of Ship Mechanics,2009,6:009.

[10]胡志強,崔維成.多學科優化設計在緩沖球鼻首設計中的應用[J].中國造船,2009,50(3):32-39. Hu Zhiqiang,Cui Weicheng.Application of multidisciplinary design optimization to soft bow design[J].Shipbuilding of China,2009,50(3):32-39.

[11]Liu Wei,Cui Weicheng.Multidisciplinary Design Optimization(MDO):A promising tool for the design of HOV[J].Journal of Ship Mechanics,2004,8(6):95-112.

[12]劉 蔚.多學科設計優化方法在7000米載人潛水器總體設計中的應用[D].上海交通大學,2007. Lui Wei.Application of MDO method to 7000 m HOV general design[D].Shanghai:Shanghai Jiao Tong University,2007.

[13]趙 敏,崔維成.BLISCO方法在載人潛水器設計中的應用[J].船舶力學,2009,13(2):259-268. Zhao Min,Cui Weicheng.Application of BLISCO to the multidisciplinary design of a HOV[J].Journal of Ship Mechanics, 2009,13(2):259-268.

[14]馮佰威,劉祖源,常海超.多學科設計優化技術在船舶初步設計中的應用[J].中國造船,2009,50(4):109-116. Feng Baiwei,Liu Zuyuan,Chang Haichao.Application of multi-disciplinary design optimization techniques in ships’preliminary design[J].Shipbuilding of China,2009,50(4):109-116.

[15]楊希祥,張為華.基于改進協同優化方法的固體運載火箭多學科設計優化[J].固體火箭技術,2011,34(6):671-676. Yang Xixiang,Zhang Weihua.Multidisciplinary design optimization of solid launch vehicles based on collaborative optimization[J].Journal of Solid Rocket Technology,2011,34(6):671-676.

[16]吳文瑞,黃 海,吳蓓蓓.遙感衛星總體參數設計的建模與協同優化[J].北京航空航天大學學報,2012,38(010): 1363-1368. Wu Wenrui,Huang Hai,Wu Beibei.Modeling and collaborative optimization of remote sensing satellite system parameters design[J].Journal of Beijing University,2012,38(010):1363-1368.

[17]Songlin W P Z,Guangqiang W U.Multidisciplinary design optimization of vehicle body structure based on collaborative optimization and multi-objective genetic algorithm[J].Journal of Mechanical Engineering,2011,2:017.

[18]宋保維,杜 偉,高智勇,等.基于協同優化的魚雷多學科設計優化[J].魚雷技術,2009,17(006):7-11. Song Baowei,Du Wei,Gao Zhiyong,et al.Multidisciplinary design optimization of torpedo general design based on collaborative optimization[J].Torpedo Technology,2009,17(006):7-11.

[19]賀 謙,李元生,敖良波,等.渦輪葉片并行子空間多學科設計優化[J].機械設計與研究,2010,26(002):106-109. He Qian,Li Yuansheng,Ao Liangbo,et al.Concurrent subspace multidisciplinary design optimization for turbine blade [J].Machine Design and Research,2010,26(002):106-109.

[20]操安喜,崔維成.潛水器多學科設計中的多目標協同優化方法[J].船舶力學,2008,12(2):294-304. Cao Anxi,Cui Weicheng.Multi-objective collaborative optimization in multidisciplinary design for submersible[J].Journal of Ship Mechanics,2008,12(2):294-304.

[21]陳爐云,侯國華,張裕芳.協同優化理論在多破損模式結構分析中的應用[J].中國造船,2012,53(2):88-95. Chen Luyun,Hou Guohua,Zhang Yufang.Application of collaborative optimization theory to multiple damage model of structure[J].Shipbuilding of China,2012,53(2):88-95.

[22]黃海燕,林志祥,王德禹.船艉結構靜動態多目標優化設計[J].船舶力學,2011,15(11):1271-1277. Huang Haiyan,Lin Zhixiang,Wang Deyu.Multi-objective optimization of ship stern under static and seismic loading[J]. Journal of Ship Mechanics,2011,15(11):1271-1277.

[23]Kodiyalam S.Evaluation of methods for multidisciplinary design optimization(MDO),Phase I[M].National Aeronautics and Space Administration,Langley Research Center,1998.

[24]蔣 平,匡 玲,邵新宇,等.基于近似模型的兩級集成系統協同優化方法[J].中國機械工程,2012,23(004):395-402. Jiang Ping,Kuang Ling,Shao Xinyu,et al.A new BLISCO method based on approximate models[J].China Mechanical Engineering,2012,23(004):395-402.

[25]Zhao M,Cui W.Application of the optimal Latin hypercube design and radial basis function network to collaborative optimization[J].Journal of Marine Science and Application,2007,6(3):24-32.

[26]張 靜,李柏林,張衛華,等.基于Kriging模型的改進協同優化算法[J].西南交通大學學報,2010,45(004):539-543. Zhang Jing,Li Bailin,Zhang Weihua,et al.Improved collaborative optimization algorithm[J].Journal of Southwest Jiaotong University,2010,45(004):539-543.

[27]李海燕,井元偉,張聞雷.基于遺傳算法的協同優化方法[J].東北大學學報:自然科學版,2009(008):1074-1077. Li Haiyan,Jing Yuanwei,Zhang Wenlei.A new collaborative optimization based on genetic algorithm[J].Journal of Northeastern University:Natural Science,2009(008):1074-1077.

[28]Li X,Li W,Liu C.Geometric analysis of collaborative optimization[J].Structural and Multidisciplinary Optimization, 2008,35(4):301-313.

[29]Alexandrov N M,Lewis R M.Analytical and computational aspects of collaborative optimization for multidisciplinary design[J].AIAA Journal,2002,40(2):301-309.

[30]Braun R D,Gage P J,Kroo I M,et al.Implementation and performance issues in collaborative optimization[J].AIAA Paper,1996(96-4017).

[31]韓明紅,鄧家禔.協同優化算法的改進[J].機械工程學報,2007,42(11):34-38. Han Minghong,Deng Jiati.Improvement of collaborative optimization[J].China Mechanical Engineering,2007,42(11): 34-38.

[32]Holtrop J,Mennen G G.An approximate power prediction method[J].International Shipbuilding Progress,1982,29(335): 166-170.

[33]黃宏波.船舶設計實用手冊總體分冊[M].北京:國防工業出版社,1998. Huang Hongbo.Ship design handbook[M].Beijing:National defense of Industry Press,1998.

[34]范尚雍.船舶操縱性[M].北京:國防工業出版社,1988. Fan Shangyong.Ship maneuverability[M].Beijing:National defense of Industry Press,1998.

Application of improved multi-discipline collaborative optimization in ship conceptual design based on dynamic penalty factors

ZHOU Qi1,2,JIANG Ping2,XU Hui2,CHEN Li2,HUANG Wei-gang2
(1.School of Mechanical Science and Engineering,Huazhong University of Science&Technology, Wuhan 430074,China;2.China Ship Development and Design Center,Wuhan 430064,China)

Facing the shortcomings of traditional collaborative optimization,such as time-consuming,being sensitive to the initial points and not converging.An improved collaborative optimization is presented and then is applied to ship conceptual design.The main feature of the proposed method is converting systemlevel consistency constrained optimization problem to an unconstrained optimization problem based on penalty function.To ensure the efficiency of the proposed method,two types of dynamically adjustable penalty factors which always reflect the different information are presented.The effects of dynamically adjustable penalty factors are reflected in the optimization process.In the early stage,the larger the difference between the system-level design variables and discipline shared variables is,the larger the punishment is.So that the consistency difference would dominate the overall objective function and prompt the consistency differences decline rapidly.As the process of optimization,dynamically adjustable penalty factors decreased,the convergence of the objective function would be accelerated.Comparing with the traditional collaborative optimization and other typical improved methods via a numerical example,the better convergence,stability andreliability of the presented collaborative optimization are demonstrated.Finally,this improved collaborative optimization is used to solve an oil tank conceptual design optimization problem that with a cost system and four performance sub-disciplines and a satisfied optimization result is also achieved.

multi-discipline design;collaborative optimization;penalty factor;discrepancy information; conceptual design of ship

U662 TP301.6

：A

10.3969/j.issn.1007-7294.2016.10.007

1007-7294（2016）10-1269-12

2016-03-20

國家青年科學基金項目（51505163）；國防基礎科研重點項目（A0820110001）

周 奇（1990-），男，碩士；蔣 平（1981-），男，副教授，通訊作者，E-mail:chuanbo701@126.com。