立式加工中心支承系統敏感性分析及其結構設計*

馬雅麗，馮　瀟

(大連理工大學 機械工程學院，遼寧 大連　116024)

?

立式加工中心支承系統敏感性分析及其結構設計*

馬雅麗，馮瀟

(大連理工大學 機械工程學院，遼寧 大連116024)

摘要：為了高效溯源出機床支承系統的剛性薄弱環節，提出了敏感性分析基礎上面向支承系統加工精度的結構設計方法。基于敏感性分析結果，以支承系統加工精度影響明顯的立柱為例進行了拓撲優化設計，提出了以靜態應變能與靜動組合應變能為優化目標響應的壁板與結構單元設計。在此基礎上，將該機床的刀尖最大變形量作為優化設計的目標，兼顧支承系統的質量與固有頻率，建立了支承系統中涉及立柱外壁板和結構單元的尺度優化設計方法。最后，立式加工中心支承系統在保證質量相對不變的條件下，對比分析了新設計方案與原方案的性能，其結果剛性提高了5%~11%，驗證了支承系統敏感性分析方法及結構設計的有效性。

關鍵詞：加工中心；支承系統；敏感性分析；拓撲優化；尺度優化

0引言

機床結構設計方法主要通過傳統設計及改進、優化設計法、仿生法以及替換傳統材料等達到機床性能的最佳化[1],而如何將現代科學技術應用于機床的設計開發、分析評估、改進優化是當前研究機床結構設計的關鍵問題之一。

目前機床結構優化設計的研究主要包括以下兩個方面：一方面基于有限元分析的機床結構拓撲優化，在生成的概念模型基礎上進行尺寸和形貌的局部設計[2-3]；另一方面基于相關的優化算法進行外形和尺寸優化[4]。

針對機床敏感性分析來說，黃強[5]介紹了基于多體系統理論與齊次坐標變換方法，提出了從眾多機床幾何誤差源中識別出對加工精度影響較大的敏感性誤差。程強[6]在敏感性分析的基礎上提出一種識別關鍵性幾何誤差源參數的新方法，并采用矩陣微分法計算和分析誤差敏感性系數。范晉偉[7]提出了一種基于多體系統運動學理論的機床誤差敏感性分析新方法。

盡管機床的敏感性分析方面取得了長足的發展，但缺乏從機床結構設計角度出發，探究支承件位移參數與機床加工精度的關聯關系。在此背景下，本文以某立式加工中心為例，專注于該支承系統敏感性分析及其結構優化設計，從而可有效避免機床結構的盲目改進。

1支承系統的敏感性建模與分析

機床支承系統靜態性能的優劣是保證機床加工精度的基本要求。機床支承系統的敏感性分析旨在辨識各支承件位移參數對刀具和工件成形點相對其理想位置的影響程度，探究支承件位移參數與機床加工精度的關聯程度。

1.1支承系統的敏感性建模

以立式加工中心靜態位移參數作為設計變量，研究各相鄰支承件之間位移數學關系[8]及其加工精度與支承件位移參數的映射關系。基于多體系統的精度建模理論[9-10]，構建機床加工精度與各支承件位移間的數學模型，實現機床支承系統的敏感性分析。立式加工中心支承結構構成及其鄰接關系如圖1所示。

圖1　立式加工中心結構構成

立式加工中心的刀具成形點與工件成形點之間的相對位置決定了機床加工精度。加工中心的支承系統建立兩類坐標系：系統坐標系CS0和支承件坐標系CSi(i=1,2…7)。設在初始空載條件下，兩類坐標系位姿狀態重合，方向與機床坐標系方向一致。切削載荷下，機床支承系統位移是由各支承件位移相互耦合作用而產生，定義位置矢量進行描述。每個支承件坐標系i在工作空間具有三項位置位移與轉角位移參數為：

(1)

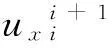
因該立式加工中心支承系統由7個支承件構成，若以床身為基準，機床支承系統的位置矢量則包含36項位置和轉角位移分量，則其位置矢量為：

E=F(U)

(2)

U=(u1,u2,u3,u5,u6)T

(3)

式中U—機床位置和轉角位移分量組成的矢量。

(4)

在切削加工工況下，刀具與工件切削加工點將發生位置偏移，其空間位置矢量E：

(5)

1.2支承系統的敏感性分析

機床支承系統位移敏感性分析的目的是溯源機床的剛性薄弱環節，以通過薄弱結構的再設計提升機床靜態性能及加工精度。其方法或過程是將靜態整機加工精度以刀具與工件兩端點的矢量差表征，分析各支承件位移參數對加工精度的效應。

根據式(5)中支承系統空間位置矢量，任意位移參數的增量所引起的機床系統空間位置變化量dE可以表達為：

(6)

若分析某一位移參數對機床支承系統位移矢量E的影響，可固定其余位移參數，則機床敏感性數學模型化簡為：

(7)

由于E為4維列向量，實際需要求出36項位置和轉角位移的單位增量對Ex、Ey、Ez產生的影響，因此可以用雅克比矩陣表示：

(8)

矩陣中各項表示機床加工精度對相應位移參數的敏感系數(SC)，并定義為：

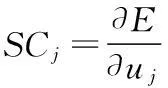
(9)

其中SCj,SCXj,SCYj,SCZj(j=1,2,3……36)代表機床支承件各位移參數uj影響E、Ex、Ey、Ez的敏感系數。

限于篇幅，本文以常用銑削平面工況的加工敏感方向z向為例，通過敏感系數的大小來辨別支承件位移參數對機床z方向加工精度的影響程度。為便于分析，對敏感分析數據進行歸一化處理：

(10)

為評價立式加工中心支承件位移參數對支承系統綜合位移的影響程度，建立立式加工中心z向的敏感因子為：

(11)

式中uj為位移參數；δ為位移參數的敏感因子。

采用有限單元法分析立式加工中心整機靜態性能，提取各支承件的相對位移參數代入敏感性模型，完成立式加工中心z向敏感因子分析，其結果如圖2所示。z向敏感因子反映了該立式加工中心支承結構對于z向加工精度的影響程度。分析結果表明，立柱z向位置位移的敏感因子占全部敏感因子的35%，而床身前部(即與十字滑臺結構相連接的部分)和工作臺z向位置位移的敏感因子不足2%。基此，獲得支承系統z向薄弱結構，可通過再設計進一步提高相關結構的性能。

圖2　立式加工中心z向敏感因子

2支承結構的拓撲優化設計

立式加工中心的立柱主要結構由實體壁板、筋板以及鑲嵌壁板上的結構單元組成。為獲得最優的支承系統性能，采用以靜態與動態性能多目標的結構拓撲優化技術進行結構壁板及筋板的主體結構設計；基于立柱的承載類型，選擇結構單元類型；利用尺度優化方法獲得主要結構參數的尺寸，從而綜合提升支承件的性能。

2.1支承結構的壁板設計

機床立柱需要經歷多加工工況載荷條件，因此采用加權來分析與設計工況。根據立柱支承功能和固定型式，設置導軌、軸承座與螺釘固定連接板為非設計區域，其余部分為優化設計區域，獲得具有良好綜合性能的最佳傳力路徑，如圖3所示。

綜合考慮圖3動靜拓撲優化獲得的傳力路徑，設計立柱壁板的外部形狀。新結構與原模型外壁板的承載路徑基本一致，呈現“梯形”的結構形式，并基此確定立柱外壁板的形狀尺寸。

圖3　立柱外壁板的基本形狀

2.2支承結構的結構單元設計

支承結構的結構單元設計是將結構單元附著在相應的內壁板，防止空心薄壁結構產生顫振和剛性不足的有效措施。通過壁板內壁布置相應的結構單元把導軌引進的集中載荷轉移和分散到立柱的整個截面板壁上，實現立柱的整體剛性增強。

結構單元類型的選擇首先應參考拓撲優化結構中局部單元的形式，抽象并規整化；其次，根據支承結構的承載類型，以及結構單元在同尺寸下不同單元類型的力學性能，綜合考慮最優的單元類型；最后，盡可能地采取對稱分布有序布置結構單元，從而簡化鑄造結構工藝性以及熱量傳遞能力。

立柱新結構方案如圖4所示。根據拓撲優化材料分布，選擇太陽型結構單元附著于后壁板相應位置處，以滿足拓撲結構中力的最佳傳遞路徑；同時參考文獻結果[11]，由于菱型與米字型單元結構具有一定的相似性，并且在抗彎、扭等各項性能突出，選擇性能略高的菱型單元布置在立柱導軌四周的壁板上，加強立柱懸臂部分的局部剛度，避免薄壁振動。

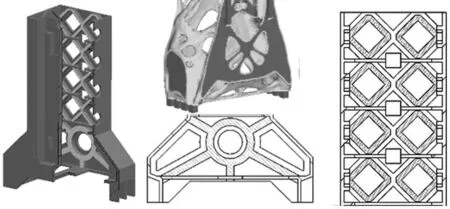
圖4　立柱的結構單元

3支承結構的尺度優化設計

支承結構的尺度優化設計是基于Workbench與Pro/E實現聯合參數化建模與分析，采用多變量多目標優化的設計方法，在支承系統的基礎上，通過結構性能最薄弱的立柱尺寸優化，選擇合理的外壁板、加強筋和結構單元尺度，以滿足支承系統的靜動態性能。

3.1支承結構的尺度優化目標與變量

將該機床的刀尖最大變形量作為立柱尺度優化設計的優化目標，保證在質量不變或者減小的條件下，改善支承系統的靜態性能。同時，建立對稱性和工藝性約束，設置優化變量中相應尺寸保持等量關系，亦可顯著減小計算量。立柱優化以外壁板的前后側、左右側、加強筋厚度和菱型單元的寬度與高度五種尺寸作為優化變量，如圖5所示。此外，對以系統模態固有頻率作為衡量該立式加工中心動態性能的優化目標，分析優化變量參數與固有頻率的關系。

圖5　立柱尺寸優化變量

3.2支承結構的尺度優化結果分析

根據workbench正交試驗，通過響應曲面(線)來擬合設計點，研究優化變量的影響，并能夠動態顯示優化變量與目標參數之間的關系，確定最佳的優化變量尺寸。限于篇幅，僅列舉其中的兩種優化變量如圖6所示，圖中x、y和z分別代表加強筋厚度、菱型單元高度以及刀具的z向最大變形量。

為了更好地明確優化變量對于優化目標的影響程度，基于workbench的靈敏度結果，衡量各優化變量的貢獻程度。其中，涵蓋了對模型質量和刀尖成形點位移的影響，如圖7所示。當優化變量的刀尖變形靈敏度大于其質量靈敏度時，則說明該優化變量更能夠滿足在質量輕的前提下，對機床刀尖變形量影響更大。圖中結果顯示，側壁厚度、前后壁板厚度和菱型單元高度符合刀尖變形靈敏度大于其質量靈敏度。此外，側壁板厚度、前后壁板厚度、菱型寬度、加強筋厚度以及菱型高度依次對于刀尖變形的影響逐漸減小。

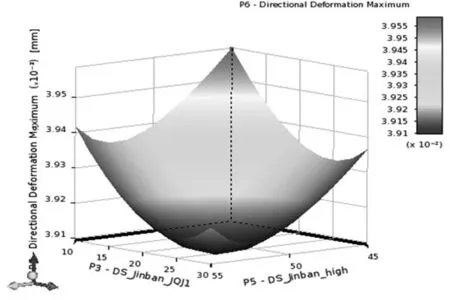
圖6　優化變量的響應曲面

圖7　優化變量的靈敏度

在考慮該支承系統導致的刀尖最大變形的同時，通過Workbench立柱外壁板、加強筋以及菱型單元的正交試驗設計，觀察立式加工中心支承系統的固有頻率，圖8為模態優化過程中不同優化變量尺寸組合的固有頻率結果。圖中的結果表明，優化變量大小的變化對支承系統的固有頻率影響較小，其固有頻率變化的最大幅度不超過1.6Hz。

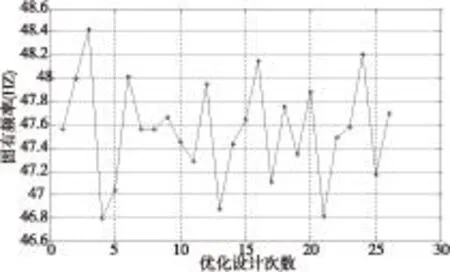
圖8　模態優化分析結果

綜上，立柱結構最終尺寸僅需要考慮各優化變量對支承系統剛性的影響，即刀尖的位移量。根據優化變量的靈敏度及響應曲面，將前后壁板厚度、側壁厚度和菱型單元寬度由初始的15mm設置為18m、28mm和12mm，菱型單元高度由40mm增至50mm，加強筋板寬度保持不變。

4支承系統的性能評價

機床支承系統剛性采用刀具成形點和工件成形點之間的相對位移誤差進行評價。由于工作臺處變形相對刀具成形點變形要小很多，因此，結構方案性能評價時，僅考慮刀具的位移量作為支承系統剛性的評價指標。

保證新結構方案與原方案的工況條件、約束位置、網格劃分等保持一致情況下進行結構的剛性分析，結果見圖9。刀具上最大位移點由53.8μm減小至48.4μm，而最小位移點則由50.0μm減小至47.4μm；其支承系統的質量3.255t減小為3.241t,即保證質量相對不變的條件下，立式加工中心支承系統的剛性提高了5%~11%左右。

圖9　支承系統的刀具位移

5結論

本文從機床結構設計角度出發，提出了切削載荷下支承系統的敏感性建模與分析方法，結果顯示，立柱z向位置位移是該立式加工中心支承系統的薄弱環節；基于此，建立了立柱的拓撲優化與在支承系統基礎上尺度優化設計方法，優化的結果顯示，立柱的優化變量對機床系統固有頻率的影響很小；最終在保證質量相對不變的條件下支承系統的剛性提高了5%~11%左右。

[參考文獻]

[1] Ma Y L, Gong Z, Ma C. Structure Design of a Machining Center Bed Based on Topology Optimization Technique[J]. Applied Mechanics and Materials. 2014, 490: 580-585.

[2] Spath D, Neithardt W, Bangert C. Integration of topology and shape optimization in the design process[C]. 2001.

[3] 馬超，馬雅麗，趙宏安，等. VHT800立式車銑加工中心立柱結構靜動態優化及輕量化設計[J]. 組合機床與自動化加工技術, 2011(3): 11-15.

[4] 楊佳文，黃巧林. 大口徑反射鏡結構參數優化設計[J]. 中國空間科學技術,2011(4): 77-83.

[5] 黃強，張根保，張新玉. 機床位姿誤差的敏感性分析[J]. 機械工程學報,2009,45(6): 141-146.

[6] 程強，劉廣博，劉志峰，等. 基于敏感度分析的機床關鍵性幾何誤差源識別方法[J]. 機械工程學報,2012,48(7): 171-179.

[7] 范晉偉，王曉峰，陳東菊，等. 基于多體運動學理論的機床誤差靈敏度分析[J]. 高技術通訊,2013, 23(3): 318-324.

[8] 粟時平. 多軸數控機床精度建模與誤差補償方法研究[D]. 長沙:中國人民解放軍國防科學技術大學, 2002.

[9] 任永強，楊建國. 五軸數控機床綜合誤差補償解耦研究[J]. 機械工程學報,2004, 40(2): 55-59.

[10] 任永強，楊建國，竇小龍，等. 五軸數控機床綜合誤差建模分析[J]. 上海交通大學學報,2003, 37(1): 70-75.

[11] 邢俏芳，董惠敏，姜懷勝，等. 機床輕量化結構單元特征研究與靜態性能分析[J]. 制造技術與機床,2012(12): 44-49.

(編輯李秀敏)第3期

Sensitivity Analysis and Structure Design of Supporting System for Vertical Machining Center

MA Ya-li, FENG Xiao

(School of Mechanical Engineering, Dalian University of Technology, Dalian Liaoning 116024, China)

Abstract：Structure design method for machining precision of the supporting system is presented on the sensitivity analysis, aiming to seek the weak spots of the machine tool rigidity. Based on sensitivity analysis, the topological optimization of the column that has significantly effect on machining precision is developed so that proposes panel and unit design aiming at strain energy of the dynamic and static combination. Subsequently, considering the tool maximum deformation, weight and natural frequency of the supporting system, size optimization method involved in panel, strengthening rib and unit of the supporting system is established. Ultimately the rigidity of the supporting system can enhance 5%~11% under the condition that the weight of the supporting system is not higher than the original plan, this result can verify the effectiveness of the method on sensitivity analysis and structure design of supporting system.

Key words：machining center; supporting system; sensitivity analysis; topological optimization; size optimization

中圖分類號：TH166;TG659

文獻標識碼：A

作者簡介：馬雅麗(1963—)，女，滿族，遼寧鞍山人，大連理工大學副教授，碩士生導師，博士，研究方向為機械系統設計及創新設計理論方法，(E-mail)myl@dlut.edu.cn。

*基金項目：國家科技重大專項(2015ZX04014021,2012ZX04010-011)

收稿日期：2015-04-29

文章編號：1001-2265(2016)03-0009-04

DOI:10.13462/j.cnki.mmtamt.2016.03.003