讓“三角形成立的條件”應用的更自然
——高一（上）“研究性”公開課教學設計

◎張成鵬

讓“三角形成立的條件”應用的更自然
——高一（上）“研究性”公開課教學設計

◎張成鵬

以a，b，c為三邊長的線段構成三角形的充要條件是“任意兩邊之和大于第三邊”，還可以自然地轉化為“三條線段中最長的小于其他兩條線段的和”．本文巧妙的設計了如何將“三角形成立的條件”應用的更自然，如何更好的“轉化”為不等式組恒成立及引導學生思考“以函數值f（a），f（b），f（c）為三邊長的線段構成三角形的等價轉換”．

構成三角形；充要條件；三角形穩定函數

背景分析：筆者執教于上海市華東師范大學第二附屬中學，現所帶班級為高一理科班、科技創新實驗班，“研究性學習”經常在這兩個班級的課堂上開展．借與遼寧數學教研員考察我校的機會，開設一節題為《讓“三角形成立的條件”應用的更自然》的公開課．選擇這個題目的理由是：（1）滬教版教材中高一第二章已經介紹完不等式，第三章函數內容也已經過半；（2）高中“不等式恒成立”的數學思想學生已然接觸過；（3）利用不等式恒成立解答函數中的問題接觸較少．基于以上幾點，選擇從眾所周知的“以a，b，c為三邊長的線段構成三角形的充要條件”出發，一起探究幾個經典數學問題．

教學目標：

1．掌握以a，b，c為三邊長的線段構成三角形的充要條件；

2．理解以函數值f（a），f（b），f（c）為三邊長的線段構成三角形的等價轉換；

3．體會“不等式恒成立”的數學思想所體現的數學的“美”．

教學重點與難點：如何巧妙應用“三角形成立的條件”解答數學問題．

教學過程：直接應用、間接應用、等價轉化

環節1．回顧與思考以a，b，c為三邊長的線段構成三角形的充要條件

（3）若a＝max｛a，b，c｝，則a＜b＋c，即：三條線段中最長的小于其他兩條線段的和；

（4）若a＝min｛a，b，c｝，則a＞max｛b－c，c－b｝，即：三條線段中最短的大于其他兩條線段的差；

設計意圖：（1）引導學生回顧三條線段構成三角形的充要條件；（2）引導學生嘗試將構成三角形的條件“轉化”為數學語言；（3）引導學生思考構成三角形的其他等價條件．

環節2．“以a，b，c為三邊長的線段構成三角形的充要條件”的直接應用

問題1．設集合A＝｛（x，y）｜x，y，1－x－y是三角形的三邊長｝，則A所表示的平面區域（不含邊界的陰影部分）的面積是？

解：根據任意三角形兩邊之和大于第三邊的性質得：

設計意圖：（1）引導學生直接利用“任意兩邊之和大于第三邊”這個性質轉化為不等式組“恒成立”問題；（2）引導學生探究不等式組在平面上所表示的區域（線性規劃問題）．

a，b，c都可以成為某個三角形三邊的長？

所以根據任意三角形兩邊之和大于第三邊的性質得：

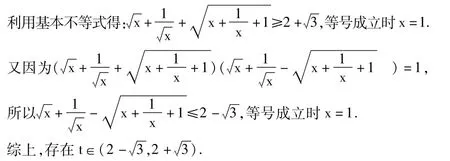
設計意圖：（1）引導學生再次直接利用“任意兩邊之和大于第三邊”這個性質轉化為不等

式組“恒成立”問題，并巧妙的等價轉化為更為簡單的兩個不等式“恒成立”問題；（2）引

導學生體會“參變量分離”的數學思想在含參變量的不等式恒成立問題中的應用．

環節3．“以a，b，c為三邊長的線段構成三角形的充要條件”的間接應用

問題3．已知三個正數a，b，c，對于任何正整數n，都有以an，bn，cn為邊長的三角形，證明：這些三角形都是等腰三角形．

證明：（法一）不失一般性，設a≥b≥c．因為對于任何正整數n，都有以an，bn，cn為邊長的三角形，所以根據三條線段中最長的小于其他兩條線段的和這個性質有an＜bn＋cn，n∈N*．（i）若三個正數a，b，c中有兩個相等，則結論成立；

綜上，這三個正數a，b，c中必有兩個相等，即這些三角形都是等腰三角形．

（法二）不失一般性，設a≥b≥c．因為對于任何正整數n，都有以an，bn，cn為邊長的三角形，所以根據三條線段中最長的小于其他兩條線段的和這個性質有an＜bn＋cn，n∈N*．而an－bn＝（a－b）（an－1＋an－2b＋…＋bn－1）≥（a－b）·n·cn－1，所以得到（a－b）·n·cn－1＜cn，由a對任何正整數n都成立，可得a＝b，即這些三角形都是等腰三角形．

設計意圖：（1）引導學生從“三條線段中最長的小于其他兩條線段的和”這個性質出發思考問題；（2）引導學生欣賞數學中的“極限”思想；（3）引導學生體會“對任何正整數n都成立”這一無窮多個條件的含義．

環節4．“以函數值f（a），f（b），f（c）為三邊長的線段構成三角形”的等價轉換

問題4．一個函數f（x），如果對任意一個三角形，只要它的三邊長a，b，c都在f（x）的定義域內，就有f（a），f（b），f（c）也是某個三角形的三邊長，則稱f（x）為“三角形穩定函數”．

解：（1）設三角形的三邊長分別為a，b，c，不妨假設a≤c，b≤c，則a＋b＞c．

對于f2（x），3，3，5可作為一個三角形的三邊長，但32＋32＜52，所以f2（x）不是“三角形穩定函數”．

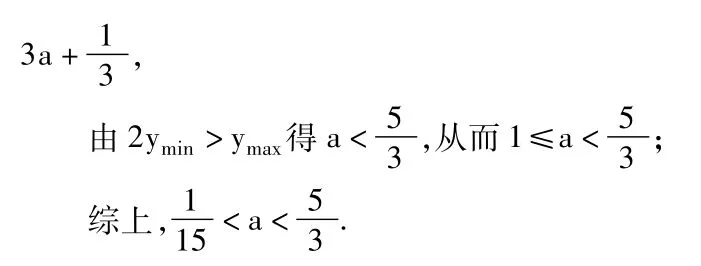
設計意圖：（1）引導學生發現并掌握以函數值f（a），f（b），f（c）為三邊長的線段構成三角

形要等價轉換為2f（x）min＞f（x）max對定義域中的x恒成立問題；（2）帶領學生再次體會

含參變量的“對勾函數”在給定區間上的最值問題．

環節5．思考

思考2．已知正數a，b，c滿足（a2＋b2＋c2）2＞2（a4＋b4＋c4），證明：以正數a，b，c為邊長的線段可構成三角形．［1］

思考3．思考以a，b，c為三邊長的線段構成銳角、鈍角、直角三角形的充要條件．

［1］計正榮．三條線段構成三角形的充要條件［J］．中等數學，1995．4

［2］黃萬堯．用三條線段為邊圍成三角形的充要條件．數學教學，1982

（作者單位：華東師范大學第二附屬中學 201203）