殺手數獨的數學模型與LINGO求解程序

柯春梅

（廈門海洋職業技術學院基礎部 福建 廈門 361101 ）

殺手數獨是一種數學智力游戲，它結合了數獨和數和的玩法。出題者將數獨的81個格子用虛線分成若干個區域，每個區域由相鄰的若干個格子組成，并在每個區域的左上角給出這個區域的所有格子內數字的總和，規定數獨參與者不僅要遵守數獨的要求，并且還要滿足各區域數字之和的要求來完成數獨題，就是在空格內填上1～9的數字，使每個數字在每一行、每一列、每個標有粗線的宮內只能出現一次，虛線框出的區域內所有數字之和等于虛線框左上角標注的數字，并且同一虛線框內的數字不能重復，這就是殺手數獨，也稱分組數字和數獨[1],[2]，圖1就是一題殺手數獨[2]。

圖1 殺手數獨

LINGO是求解優化問題的專業軟件包，它內置建模語言，提供幾十個內部函數，從而能以較少的語句，較直觀的方式描述大規模的優化模型，而且它的運算速度快，計算結果可靠[3],[4]。國內許多學者對利用計算機進行快速求解數獨的算法進行深入研究與探索，這些算法多數以回溯法為基礎，結合各種預處理提高算法的執行速度[5]-[9]，根據數獨的求解規則建立數學模型，并給予求解的研究不多[10],[11]，對于殺手數獨的建模與求解問題，目前尚未看到相關研究。

1.殺手數獨的數學規劃模型的建立過程

殺手數獨初盤沒有給定數，只給出虛線框內數字和，而虛線框所框出的區域變化無常，建立數學模型必須根據具體題目來建立，下面根據圖1所示殺手數獨分析數學模型的建立過程。

為了方便起見，（i,j）（i,j=1，2，……，9）表示數獨盤面中處于第i行第j列的格子，(m=1,2,……,9)表示第 m宮，其中 int表示向下取整。aij表示數獨初盤格子(i,j)處所填的數，其中0表示該格子未填數，殺手數獨初盤沒有給定的數，所以初盤中81個格子都填0，yij(i,j=1,2,……,9)表示數獨完成后格子(i,j)處所填的數。

引入三元0-1變量

目標函數：

數獨完成后，數獨盤上每個格子都填上 1～9的一個數字，且滿足每個數字在每一行、每一列、每個宮內不能重復，因此目標函數為

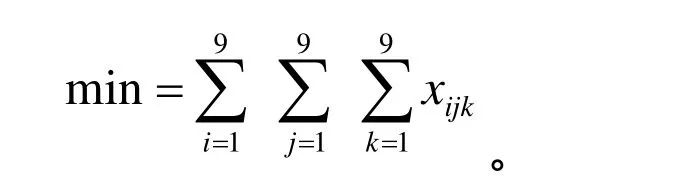
約束條件：

與決策變量的關系；

（2）每個格子（i,j)處恰好填數字 1～9中的一個數；

（3）每行1～9中的每個數只能填一次；

（4）每列1～9中的每個數只能填一次；

（5）每個宮1～9中的每個數只能填一次；

（6）xijk是0-1變量；

（7）虛線框出的區域數字之和等于虛線框左上角標注的數字，根據具體題目確定；

（8）虛線框內的數字不能重復：如果虛線框區域內的格子在同一行、同一列或者同一宮內，則他們的數字已經滿足沒有重復，如果虛線框區域內的格子至少有兩個不在同一行、同一列或者同一宮內，則應增加虛線框內的數兩兩只差的乘積的絕對值大于零作為約束條件。

因此圖1所示殺手數獨的數學模型為：

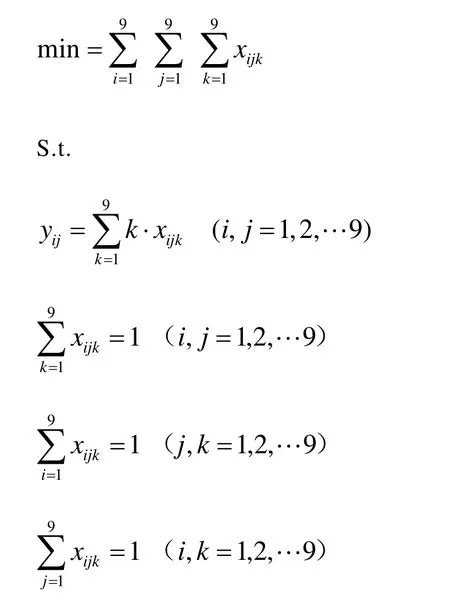
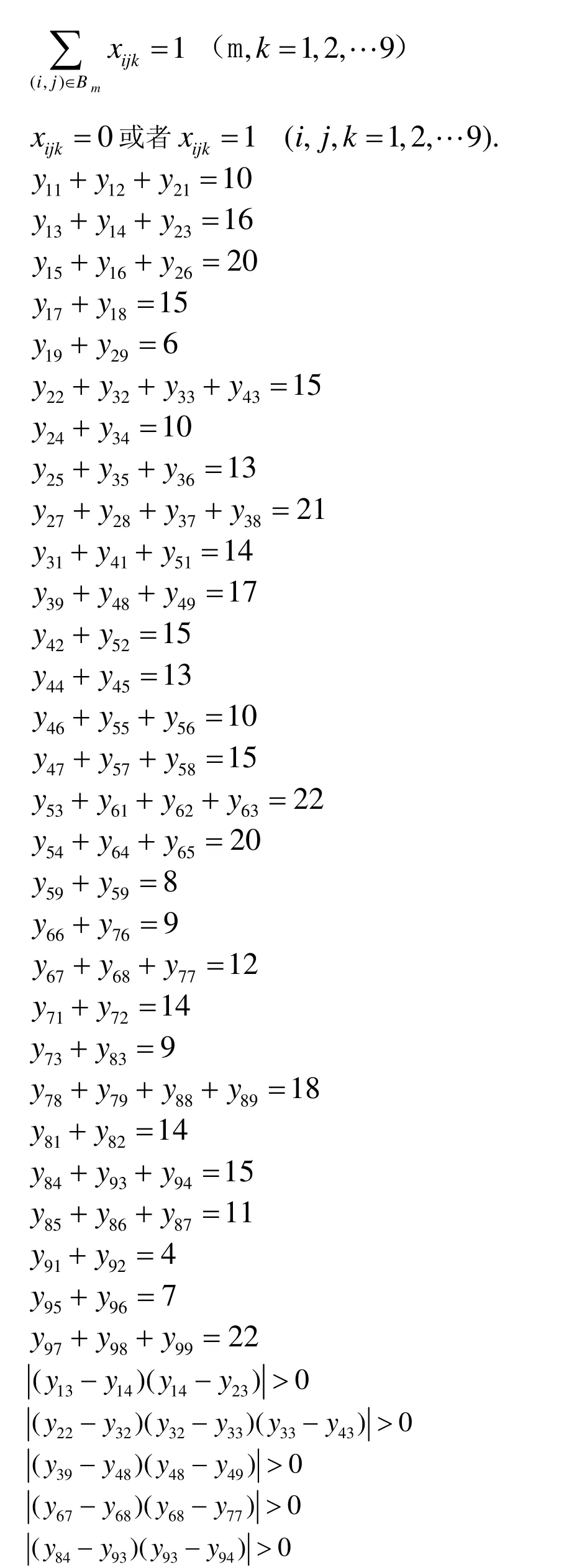
2.殺手數獨的Lingo求解程序設計

根據上述殺手數獨的數學模型，利用 LINGO軟件的內置函數@for、@sum、@floor及@abs編制求解程序，由于 LINGO軟件中“<”表示“小于等于”，“>”表示“大于等于”，因此要表示兩個數不相等，要用兩個數的差的絕對值大于一個很小的正數來表示。因此圖 1所示殺手數獨的Lingo求解程序如下：

即得到圖1所示殺手數獨的解如圖2.

圖2 殺手數獨的解

3.計算實驗

殺手數獨是一種變形數獨，對于每一題殺手數獨，目標函數都相同，約束條件中（1）～（6）是相同的，約束條件（7）和（8）則需要根據不同題目來編制。圖3、圖4、圖5所示的殺手數獨是數獨三段段位考試模擬試題，根據題目所給虛線框及其標注的數字修改LINGO求解程序，進行求解，運行后得到它的解，運算速度不足1秒，運算結果準確。

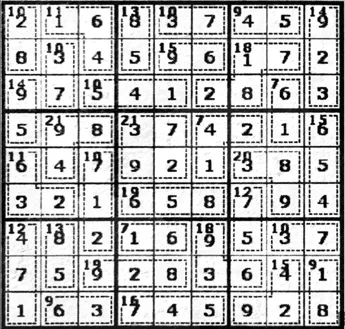
圖3 模擬試題1殺手數獨及其解

圖4 模擬試題2殺手數獨及其解

圖5 模擬試題3殺手數獨及其解

4.結語

殺手數獨作為一種數學智力游戲，既具有邏輯性、可推理性，又具有數字和的運算性，建立數學模型，利用 LINGO軟件求解大規模規劃模型的功能編制求解程序，可以快速準確地得到答案。本文以一題殺手數獨為例，建立對應的數學規劃模型，編制LINGO求解程序，快速準確得到答案，然后根據三道數獨三段段位考試模擬試題，修改部分約束條件，仍可快速準確得到答案，說明這種程序準確，同時具有可復制性。