懸挑大跨混凝土框架－剪力墻結構彈塑性分析及試驗研究

第一作者葛康男，博士生，1988年4月生

通信作者陳世鳴男，博士，教授，博士生導師，1957年生

懸挑大跨混凝土框架-剪力墻結構彈塑性分析及試驗研究

葛康，陳世鳴(同濟大學土木工程學院，上海200092)

摘要：某擬建文化藝術中心是一個具有大空間、大懸挑等特點的混凝土框架-剪力墻結構，結構一端為多層大懸挑結構，最大懸挑長度為22 m，并且在頂層中庭有30 m的大跨度區域，屬平面和立面均不規則的結構。采用NOSACAD和ABAQUS有限元程序建立整體結構分析模型，進行7度罕遇烈度下的彈塑性時程分析，研究了該結構在大震作用下的變形情況、塑性鉸的分布以及受力機理等。計算結果表明：結構的懸挑端在豎向地震作用下的動力響應顯著，剪力墻受拉損傷在結構底部和懸挑樓層處較為明顯；但在大震下層間位移角滿足規范要求；并對結構裙房截斷后的模型進行了1/30的大縮尺模擬地震振動臺試驗，驗證了截斷模型方法在本試驗中的合理性，最后根據構件的受力或損壞情況給出了設計改進建議。

關鍵詞：大懸挑結構；彈塑性時程；模型設計；地震響應；振動臺試驗

收稿日期：2014-01-02修改稿收到日期：2014-04-25

中圖分類號:TU375文獻標志碼：A

Elasto-plastic analysis and tests for a cantilevered and large-span concrete frame-wall structure

GEKang,CHENShi-ming(College of Civil Engineering, Tongji University, Shanghai 200092,China)

Abstract:A culture and art center discussed here was a RC frame-wall structure characterized with a large cantilevered length and a large space, the maximum cantilevered length was 22m and the maximum span of the large space was 30m. It was irregular both in plan and elevation. Using Nosacad and Abaqus, the structural analysis model was established in order to simulate the nonlinear behavior and study deformations, distribution of plastic hinges, and force-bearing mechanism of the structure under the rare earthquake of magnitude of 7. The analysis results showed that the cantilevered end of the structure is sensitive to vertical earthquake; tension damage mainly occurs at the bottom of the shear wall and the cantilevered stories; the maximum inter-story drifts are less than the seismic design requirement of Chinese code. A 1/30 scale model was tested on a shaking table to study the seismic behavior of this kind structure after cutting the podium of the structure, the comparison between the results before and after cutting was conducted to verify the reasonability of this design method. The test results agreed well with those of the finite element analysis. Finally, according to the response and damage results of the structure, suggestions for structure design improvment were given.

Key words:large cantilevered structure; elasto-plastic time history analysis; model design; seismic response; shaking table test

隨著城市中建筑造型的要求越來越高，越來越多新穎造型的建筑出現在世界各地，復雜高層結構的抗震設計[1-2]成為工程師們日益關切的問題。

北方城市某擬建文化藝術中心為大懸挑的框架-剪力墻混凝土結構，主體結構總高度為46.1 m，且含有一層地下室，建筑底部裙房平面尺寸為190 m×110 m，結構四周布置剪力墻并均勻到頂，主體結構在標高23.2 m處至屋頂的多層均為懸挑樓層，最大懸挑跨度22 m。結構在標高23.2 m與25.7 m處沿懸挑方向均布置12根預應力梁，截面分別為800 mm×1 400 mm與1 000 mm×1 200 mm，垂直于懸挑方向布置8根截面為600 mm×2 200 mm的預應力梁，并且在標高23.2 m處至屋頂布置多根梁上預應力柱，截面為500 mm×600 mm。結構典型樓層平面圖和立面圖如圖1、圖2所示。結構內部為框架結構為滿足建筑大空間的需要，并沿圓弧線外圈布置10根直徑為1.2 m的斜柱，內圈布置12根同直徑的直柱(見圖3)；同時結構從底面至標高38.1 m處存在大開洞部位(洞口尺寸：31.90 m×24.95 m)，頂部樓層此處設置梁上柱、梁上斜撐等特殊構件(見圖4)，具體位置可參考圖1與圖2。規范[3]中對懸挑長度大于2 m的水平懸臂構件定義為長懸臂結構，設計中應計入豎向地震的考慮。綜上，該結構具有平立面不規則、樓板不連續[4]，并且含有多處錯層，且錯層大于梁高等不規則特點。結構典型懸挑樓層的平面圖和結構整體立面圖分別如圖1和圖2所示。為研究該復雜結構在地震作用下的響應和結構薄弱環節，本文采用NOSACAD和ABAQUS有限元分析軟件對結構進行動力彈塑性時程分析并對其進行大比例縮尺的模擬地震振動臺試驗。

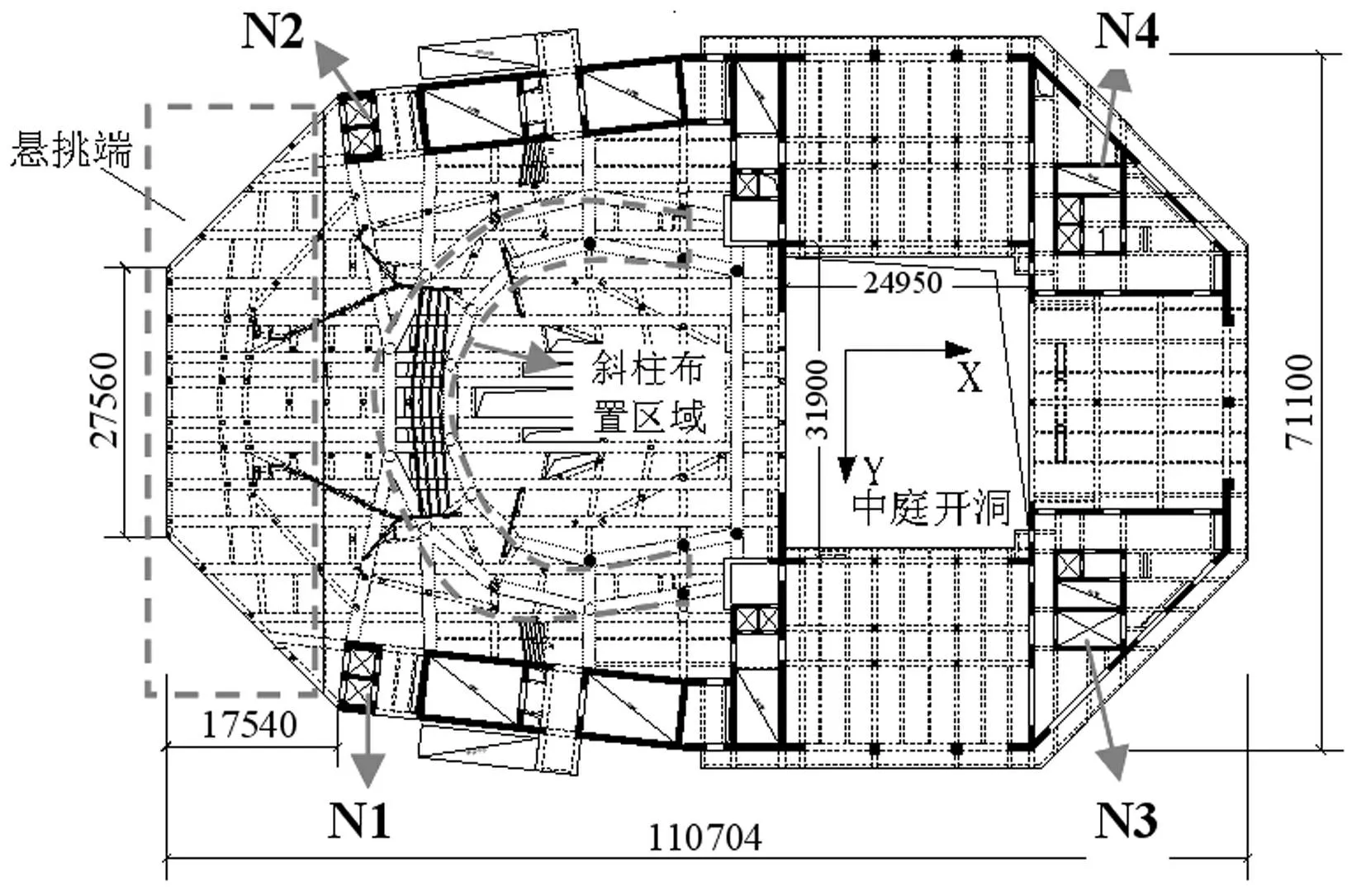
圖1　典型懸挑樓層示意圖(單位:mm) Fig.1 Typical plan of cantilever storey

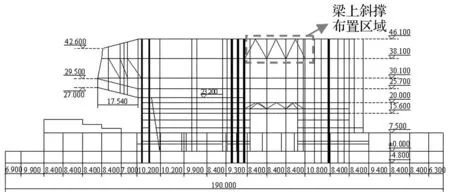
圖2　結構立面圖(單位:m) Fig.2 Elevation of the structure

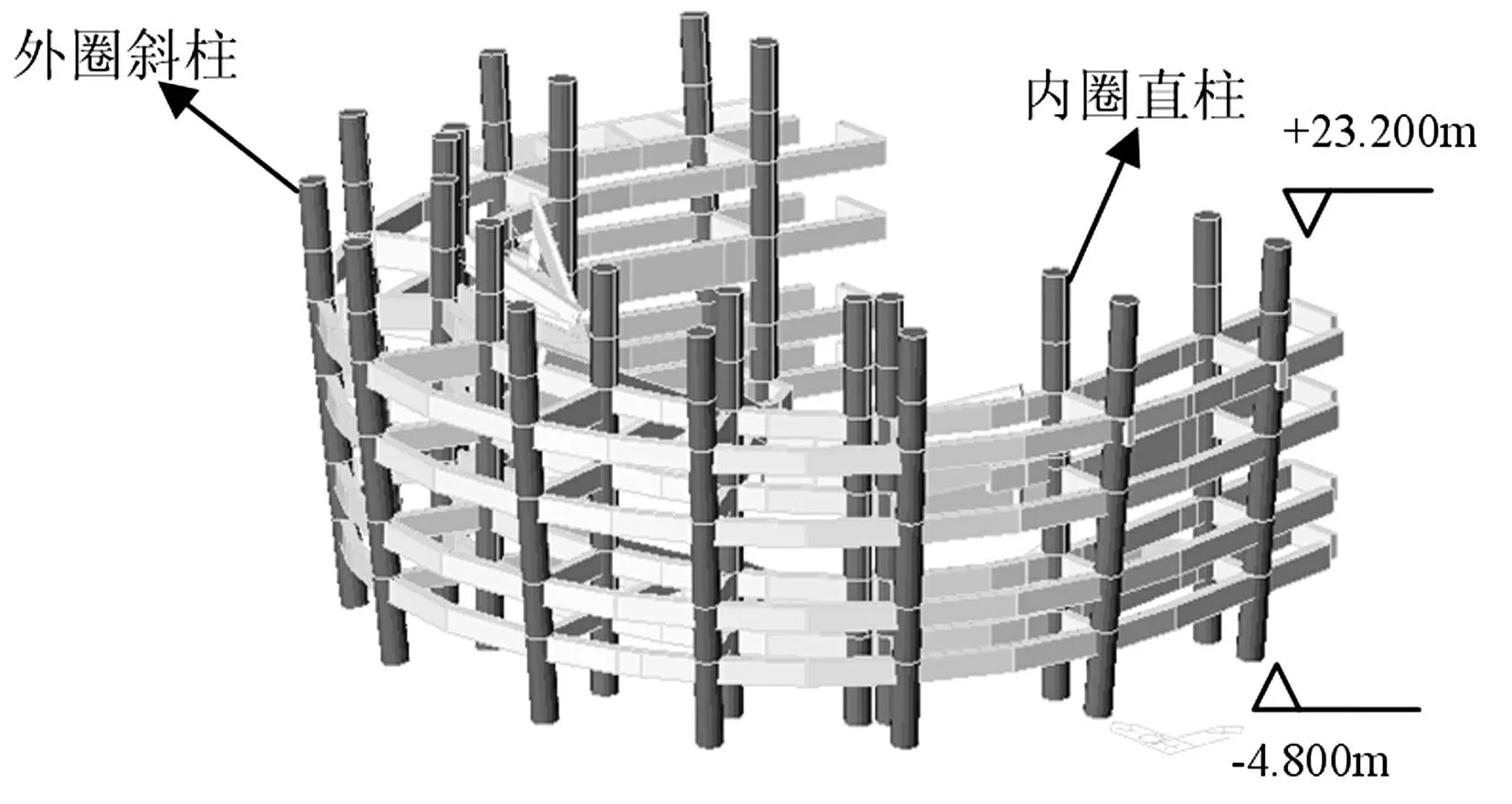
圖3　結構內部框架斜柱布置 Fig.3 Arrangement of inclined frame columns

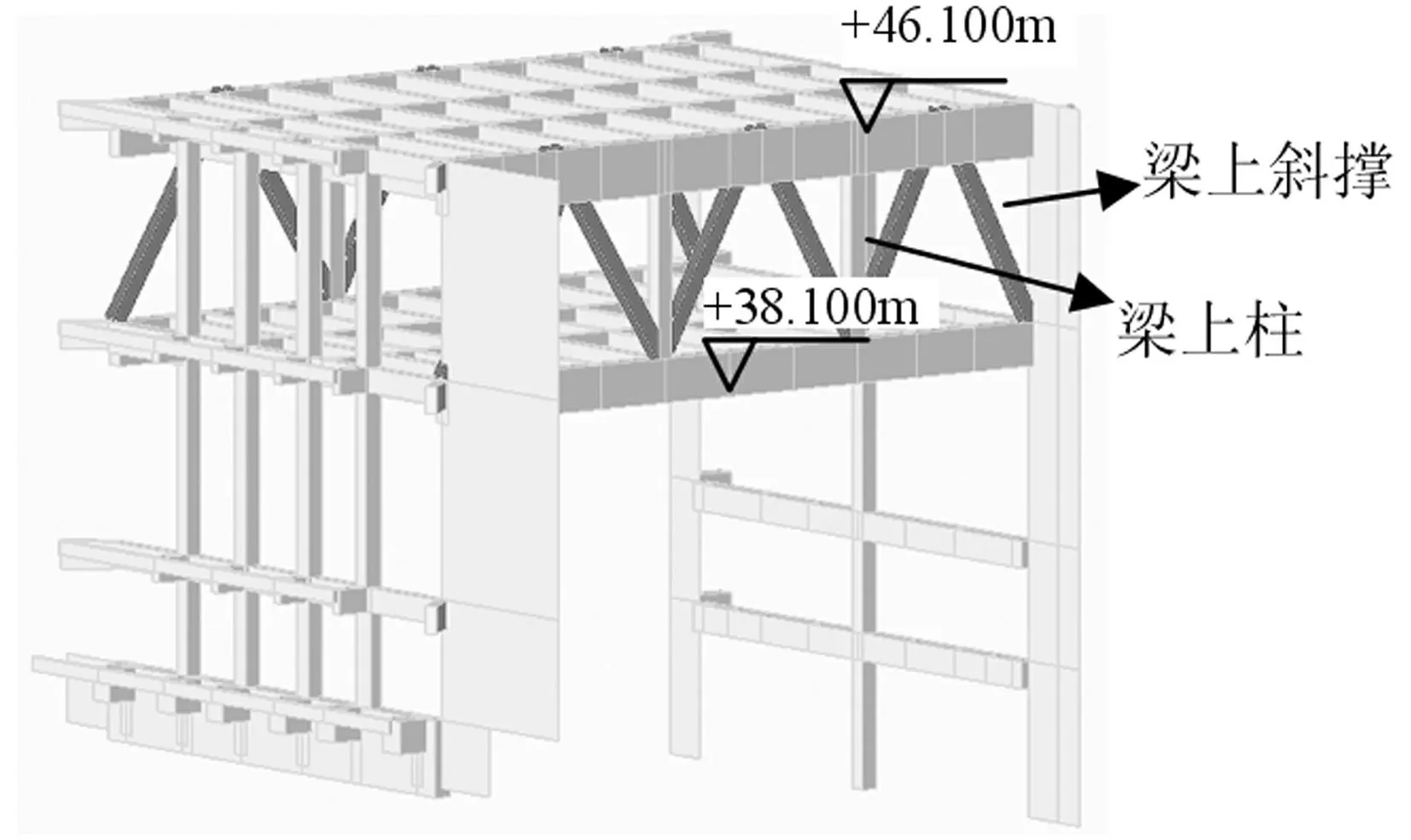
圖4　梁上斜撐及梁上柱 Fig.4 Arrangement of diagonal braces and columns on beam

1計算模型

1.1　材料信息

在對結構進行彈塑性分析時，應充分考慮材料的強度儲備，對材料均應采用規范中強度標準值進行分析計算。該結構采用C50混凝土，普通鋼筋采用HRB335和HRB400，預應力筋采用1×7AS鋼絞線，錨板等錨固裝置在模型中不予考慮。材料基本參數如表1所示。

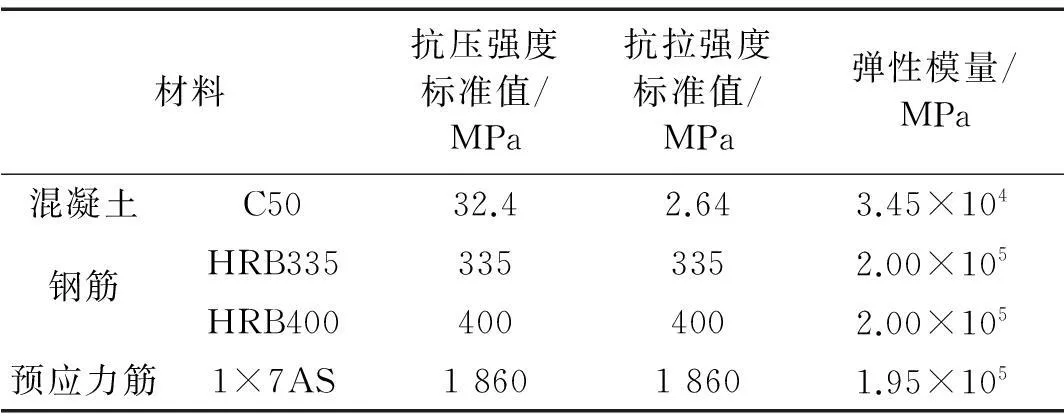
表1　材料基本參數

1.2　計算模型

本文采用同濟大學NOSACAD軟件進行分析并在后期導入到ABAQUS中。該軟件中針對梁柱桿單元采用三段變剛度模型[5]，即桿件兩端采用彈塑性單元，而桿件中部仍采用彈性單元，能有效地反映出桿件易在端部出鉸的狀況。梁單元彈塑性單元的彎矩-曲率骨架曲線采用三折線模型[6-7]，其滯回曲線如圖5所示，而框架柱中彈塑性單元由于受到軸力、彎矩的共同作用，采用纖維模型，其中混凝土的本構模型[8]如圖6所示，為簡化計算，構件中的鋼筋和鋼絞線均采用理想彈塑性的二折線模型，并考慮屈服強化，其中預應力的施加采用降溫法并在命令流中添加關鍵字進行實現。

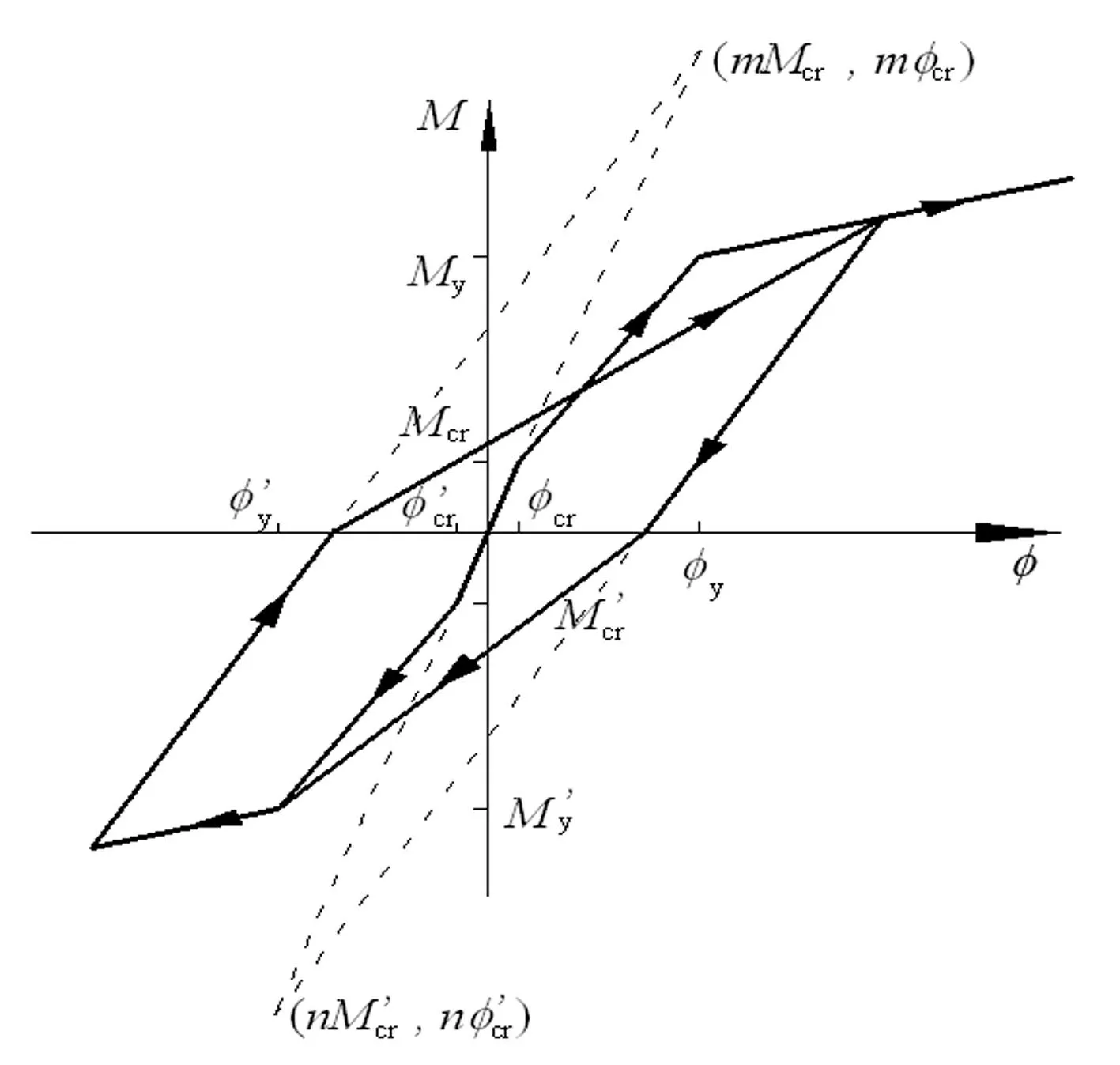
圖5　三折線彎矩-曲率滯回模型 Fig.5 Tri-linear moment curvature hysteretic model

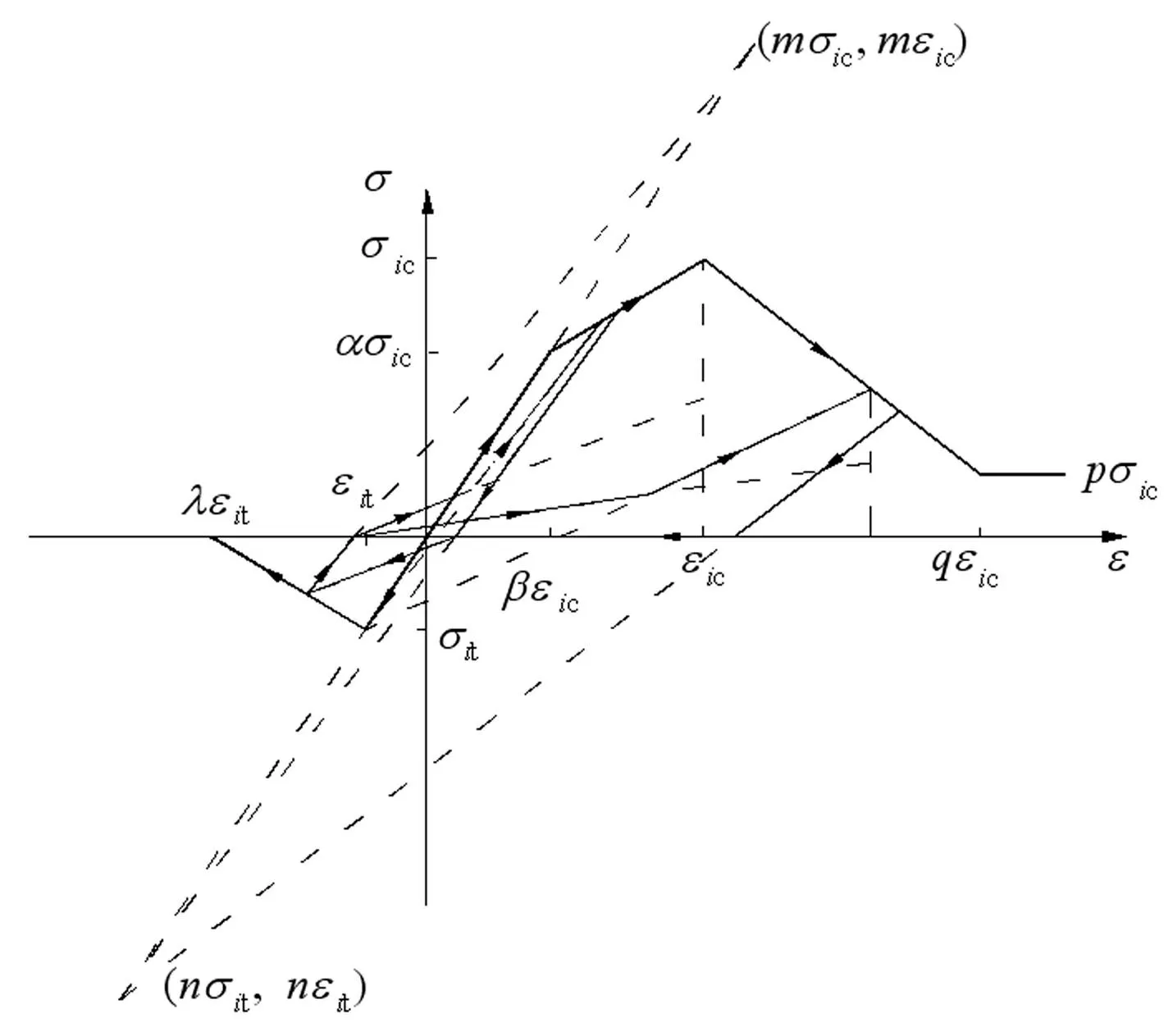
圖6　混凝土纖維本構模型 Fig.6 Concrete fiber constitutive model

1.3　結構整體模型

圖7為模型整體有限元模型示意圖，分析中采用桿單元來模擬結構中的框架梁柱，采用平面殼單元來模擬結構中的剪力墻，對樓板采用彈性材料，不考慮其塑性變化。由于考慮到模型較大，耗時較長，在非重點關注部位，僅需將墻單元網格劃分控制在2 m以內即可。

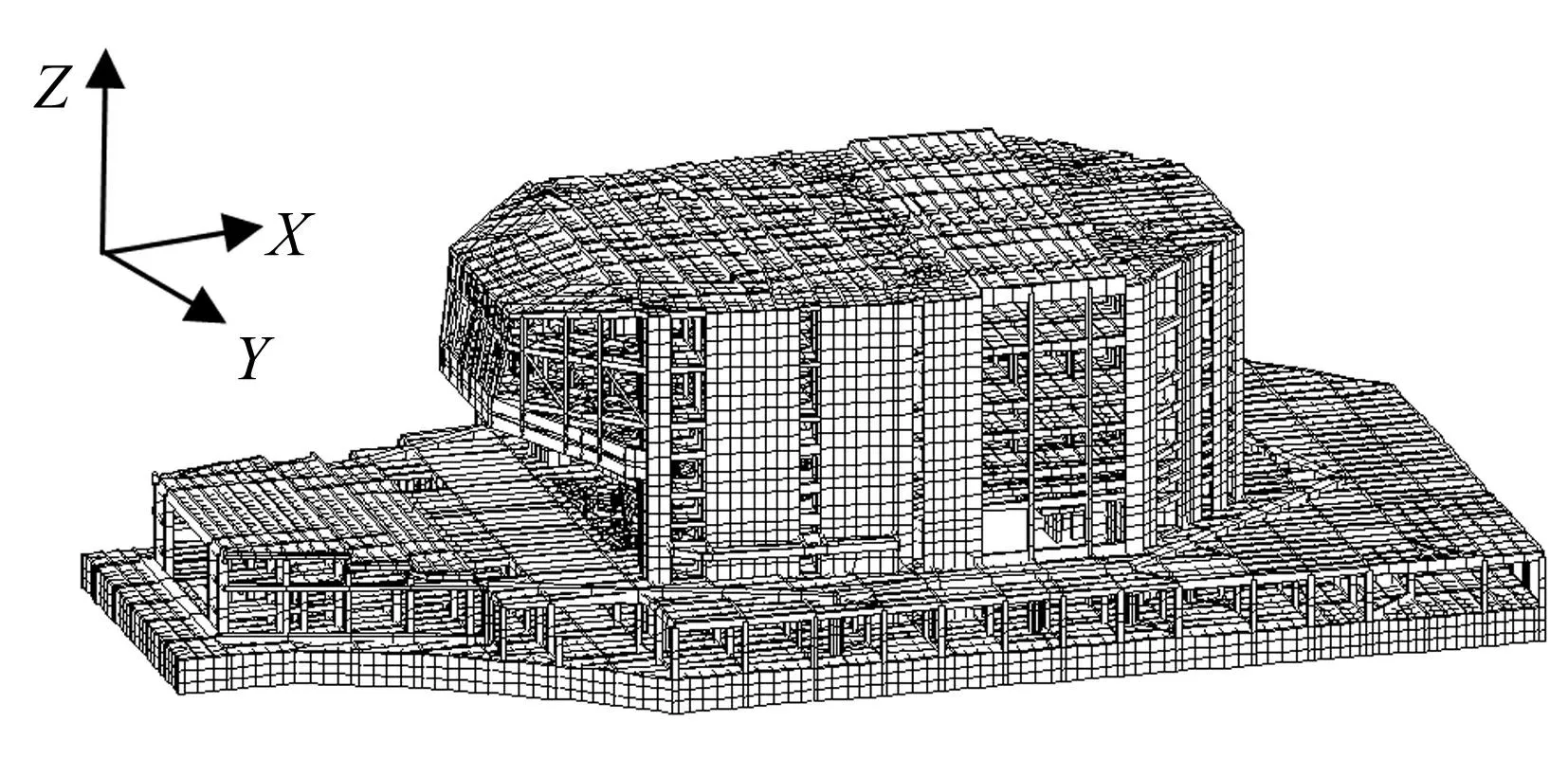
圖7　結構整體模型 Fig.7 Characteristic of whole structure

2彈塑性時程分析

2.1　自振特性

在對結構進行內力、位移等參數進行分析之前首先應對模型進行模態分析，由于該結構包含大懸挑、大跨度等特點，故要重點考慮豎向地震對結構的影響，在計算結構基本振型時要考慮豎向的整體與局部振型，需要將模型質量向X,Y,Z三向進行轉換。為了減少該結構中的局部振型，振型分析時采用了里茲向量法。計算了結構的前30階振型，結構的三向質量參與系數均達到90%，滿足計算要求。由于結構中大懸挑、大空間區域的存在，結構出現較多懸挑部分和大空間區域的局部豎向振型。圖8中(a)(b)(c)(d)所示為結構一階振型，其中(a)(b)為帶有頂部樓板局部振動的整體水平平動振型，(c)為屋頂大跨樓板的豎向局部振動，(d)為整體水平扭轉振型。

表2為NOSACAD和SATWE兩種軟件分析的結構自振周期結果，從表中結果可以看出：兩軟件計算結果存在較小誤差，是由于在SATWE中考慮了樓板剛性假定，導致結構整體較剛所致。該結構扭轉為主的第一階平動周期與以平動為主的第一自振周期之比小于規范規定的0.85,說明該結構的扭轉效應不明顯，滿足規范設計要求。

圖8　結構一階振型 Fig.8 Former four model shapes

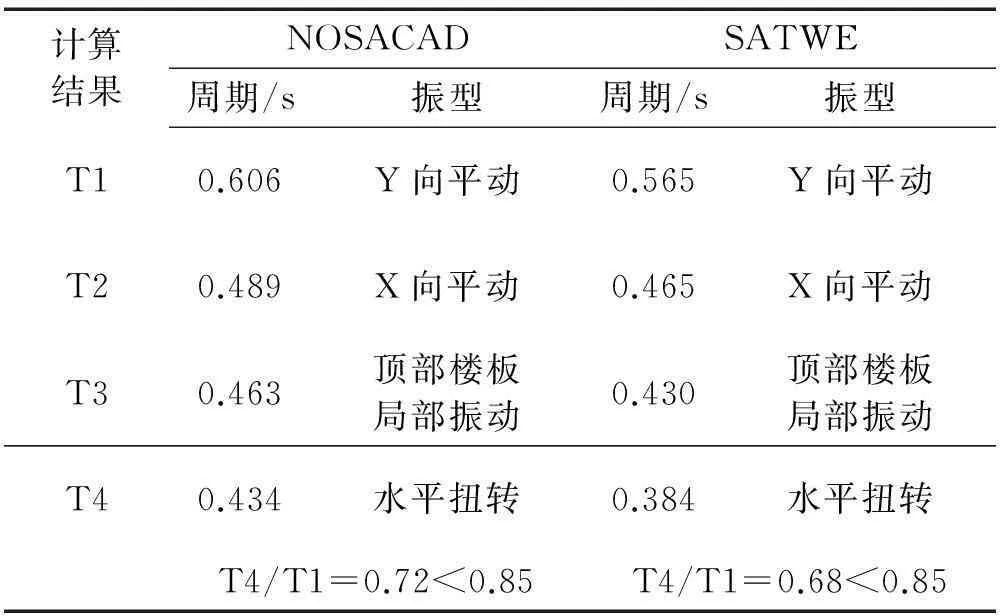
計算結果NOSACADSATWE周期/s振型周期/s振型T10.606Y向平動0.565Y向平動T20.489X向平動0.465X向平動T30.463頂部樓板局部振動0.430頂部樓板局部振動T40.434水平扭轉0.384水平扭轉T4/T1=0.72<0.85T4/T1=0.68<0.85

2.2　地震波輸入

該結構所處場地類別和設計地震分組(7度，0.10 g，Ⅱ類場地)選用兩條實際強震記錄和人工模擬地震波[9-11]進行輸入：①El-centro天然波；②Taft天然波；3)擬合設計反應譜的人工地震動SY波。其中SY人工波7度多遇水準下的加速度時程曲線和加速度反應譜分別如圖9、圖10所示。其中天然地震動按三向輸入，主方向峰值加速度為220 gal，兩水平方向和豎直方向峰值加速度峰值之比為1∶0.85∶0.65；人工波僅在水平雙向輸入，峰值加速度之比為1∶0.85。本結構中Y向側向剛度較小，故均以Y向為主方向進行輸入。

分析中的動力阻尼采用Rayleigh阻尼體系，Rayleigh阻尼包含質量阻尼α和剛度阻尼β，其與振型阻尼的換算關系如下式所示：

(1)

(2)

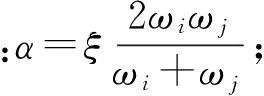
ωi,ωj為結構的圓頻率。通常情況下，ωi取結構的基頻，ωj在對結構動力反應有顯著貢獻的高階振型中選取。這種取值的結果是具有很高頻率(大于ωj)的振型反應將因其高阻尼比而被有效的消除。由于在ABAQUS中采用的是逐步積分的方法，當采用自定義材料時，不能考慮剛度阻尼，由于在本次分析中采用了自定義的混凝土本構模型，故只考慮質量阻尼。

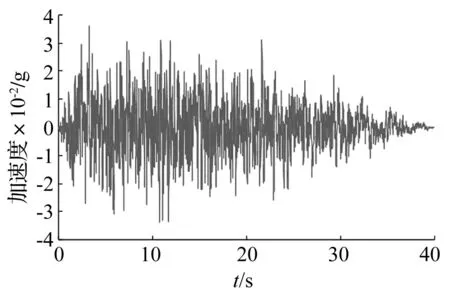
圖9　SY波加速度時程 Fig.9 Time history of acceleration of SY wave

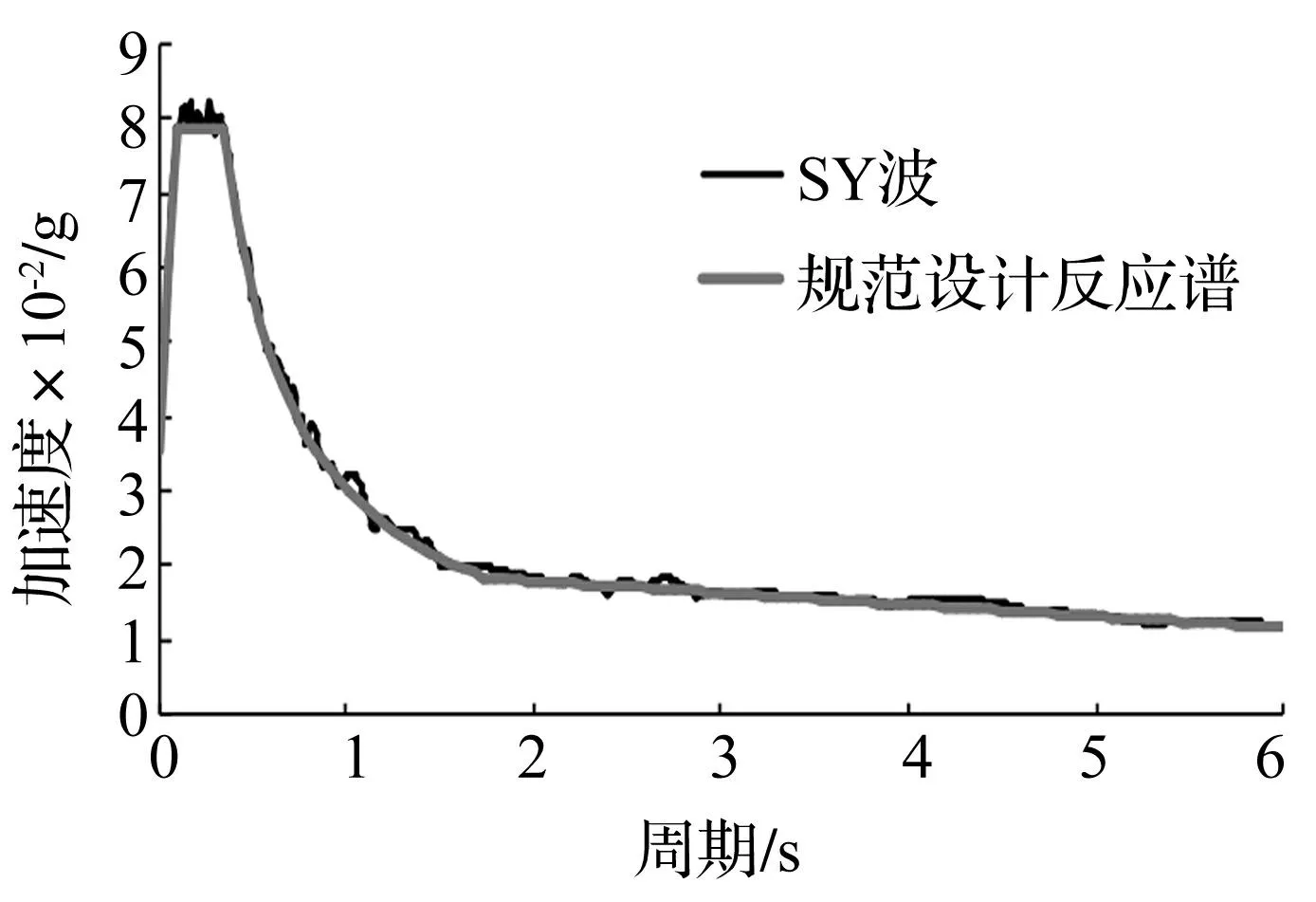
圖10　SY波加速度反應譜 Fig.10 Response spectrum of acceleration of SY wave

2.3　動力時程響應

2.3.1層間位移角響應

通過分析結構四個筒體的角點部位(見圖1)在彈性時程和彈塑性時程分析中的最大水平層間位移角來驗證結構的動力響應，以三條地震波中層間位移角響應最大的EL-centro波為例，圖11和圖12分別為7度多遇工況下和罕遇工況下的層間位移角包絡圖，其中由于N1和N3筒體靠近懸挑端，層間位移受到懸挑區域在水平方向的局部平動對剪力墻筒體產生影響。在7度多遇工況下，結構的最大彈性層間位移角為1/1026，小于規范[11]的限值1/800；在7度罕遇工況下，結構的最大彈塑性層間位移角為1/249，也小于規范的限值1/100。

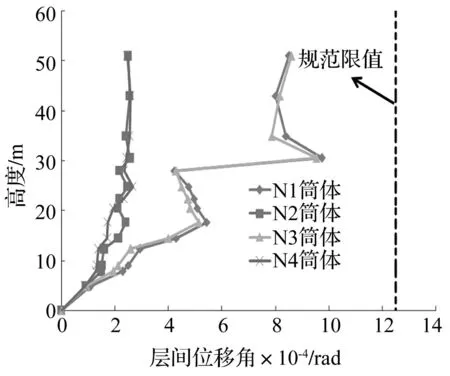
圖11　7度多遇烈度地震作用下筒體層間位移角包絡圖 Fig.11 Inter-story drift envelops of the tube under the frequent earthquake of magnitude of 7

圖12　7度罕遇烈度地震作用下筒體層間位移角包絡圖 Fig.12 Inter-story drift envelops of the tube under the rare earthquake of magnitude of 7

2.3.2懸挑端節點位移響應

對結構大懸挑端關鍵節點進行位移時程分析，圖13為懸挑端頂層的角部節點P(見圖14)在三種罕遇地震動激勵下的位移時程曲線。可以看出結構在三種峰值加速度相同的地震波作用下的水平位移響應存在較大差異，其中在Taft波激勵下的水平位移響應最小，在X和Y方向分別為34.1 mm和75.0 mm。在人工波激勵下的水平位移響應最大，在X和Y方向分別達到58.2 mm和92.0 mm。其中在EL-centro和Taft地震動激勵下的豎向位移響應也存在差別，最大豎向位移值分別為81.3 mm和63.3 mm，分別為懸挑跨度的1/185和1/237。

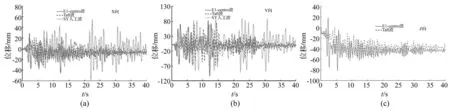
圖13　懸挑端關鍵節點位移時程圖 Fig.13 Displacement time history of corner node P

對懸挑端部的十個梁柱節點位置的位移響應進行分析(如圖14所示)，圖15為10個節點在三種地震激勵下的三向(圖中a,b,c分圖所示)位移包絡圖，可看出該十個節點在水平方向的位移值基本保持一致，懸挑頂層相對最大，在X、Y雙向分別達到61 mm，122 mm，懸挑底層最小，在X、Y雙向分別達到38 mm，61 mm；并在豎向的位移值呈現兩邊小中間大的特點形式：三個懸挑樓層位置的位移峰值相差不大，懸挑頂層峰值略大，約為115 mm，懸挑底端豎向位移約為112 mm。在豎向地震作用下，兩端的角部節點由于跟主樓的剪力墻筒體連接，約束剛度大，而中間部位節點的約

束較弱，故而在豎向激勵下的響應較大，整個懸挑部位在豎向地震的作用下呈現“拱形”的分布形態。

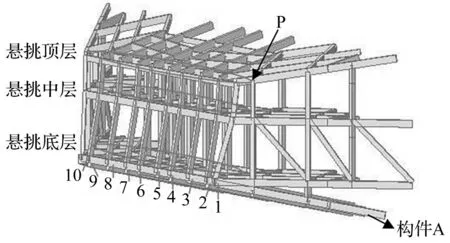
圖14　懸挑端節點示意圖 Fig.14 Sketch of cantilevered end points

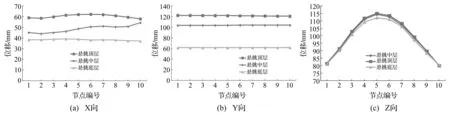
圖15　懸挑端節點位移時程包絡值 Fig.15 Displacement envelope curve of cantilevered end points

圖16給出了懸挑結構懸挑構件A(如圖14所示)在7度罕遇烈度下位移峰值隨距懸挑根部距離的變化圖，可以看出隨著距懸挑根部距離的增大，三向位移都呈現放大的趨勢：其中在水平X,Y方向懸挑末端的放大系數相對較小，分別為1.35和1.10，豎向最大位移為83.30 mm，為該構件跨度的1/181，其對應的放大系數值達到23.3。這也說明懸挑結構對豎向地震激勵的響應尤為明顯，在結構設計中應著重考慮豎向地震對懸挑部位的影響。

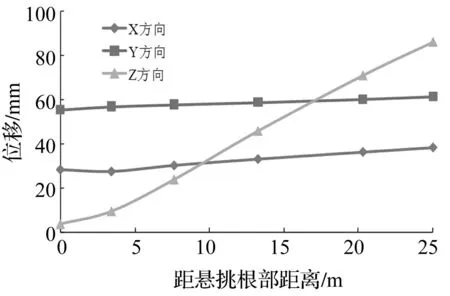
圖16　位移隨懸挑長度變化示意圖 Fig.16 Displacement-cantilever length curve of cantilevered beam A

2.3.3結構破壞形態

現對結構的損傷及破壞狀態進行分析，由于在三條地震波下結構的損傷和破壞較為類似，現以最典型的EL-centro波進行分析：由于該結構的剛度較大，在7度多遇地震作用下，結構并未出現明顯損傷情況，圖17為在7度罕遇工況中三向EL-centro波激勵下的結構破壞情況，從中可以看出，該結構中構件的塑性鉸主要出現在筒體墻片之間的連梁端部、懸挑部位的梁柱節點，屋頂大跨區域的梁端部、框架斜撐的端部，從破壞順序來看，首先是部分連梁端部出鉸，隨之結構的懸挑梁柱節點和斜撐的端部也出現塑性鉸，隨著豎向激勵越來越大，頂層大跨部位的梁端部位和懸挑區域的梁柱節點越來越多的出現塑性鉸，這也說明該部位對豎向地震的響應較為敏感。其中圖中紅色圓圈代表桿件中塑性鉸的出現。

圖18為剪力墻在三向EL-centro波激勵下7度罕遇下結構中的剪力墻出現的損傷云圖(DAMAGEC,DAMAGET分別為受壓和受拉損傷因子，介于0~1，0代表未出現損傷，1代表完全損傷)，從圖中可以看出，剪力墻的受壓損傷不明顯，僅內筒體未伸到頂部的剪力墻部位出現了受壓損傷，這也是由于四周剪力墻分布和受力均較為均勻，但在內筒體部位剪力墻布置較少，受力較為不利，且由于建筑需要，該處剪力墻未伸至結構頂層，處于一定的偏心受壓狀態所致；整體結構的剪力墻受拉損傷較為明顯，這也與后續分析中剪力墻部位的樓板向上隆起相吻合，墻體受拉損傷部位主要集中在剪力墻的底部和懸挑樓層，越靠近懸挑樓層，墻體的受拉損傷越嚴重，隨著地震的持續輸入，底部出現受拉損傷的區域不斷增加，損傷因子均大于0.7，懸挑樓層的剪力墻損傷因子已接近1，說明該部位的剪力墻已基本不能承受拉力，從而退出工作。

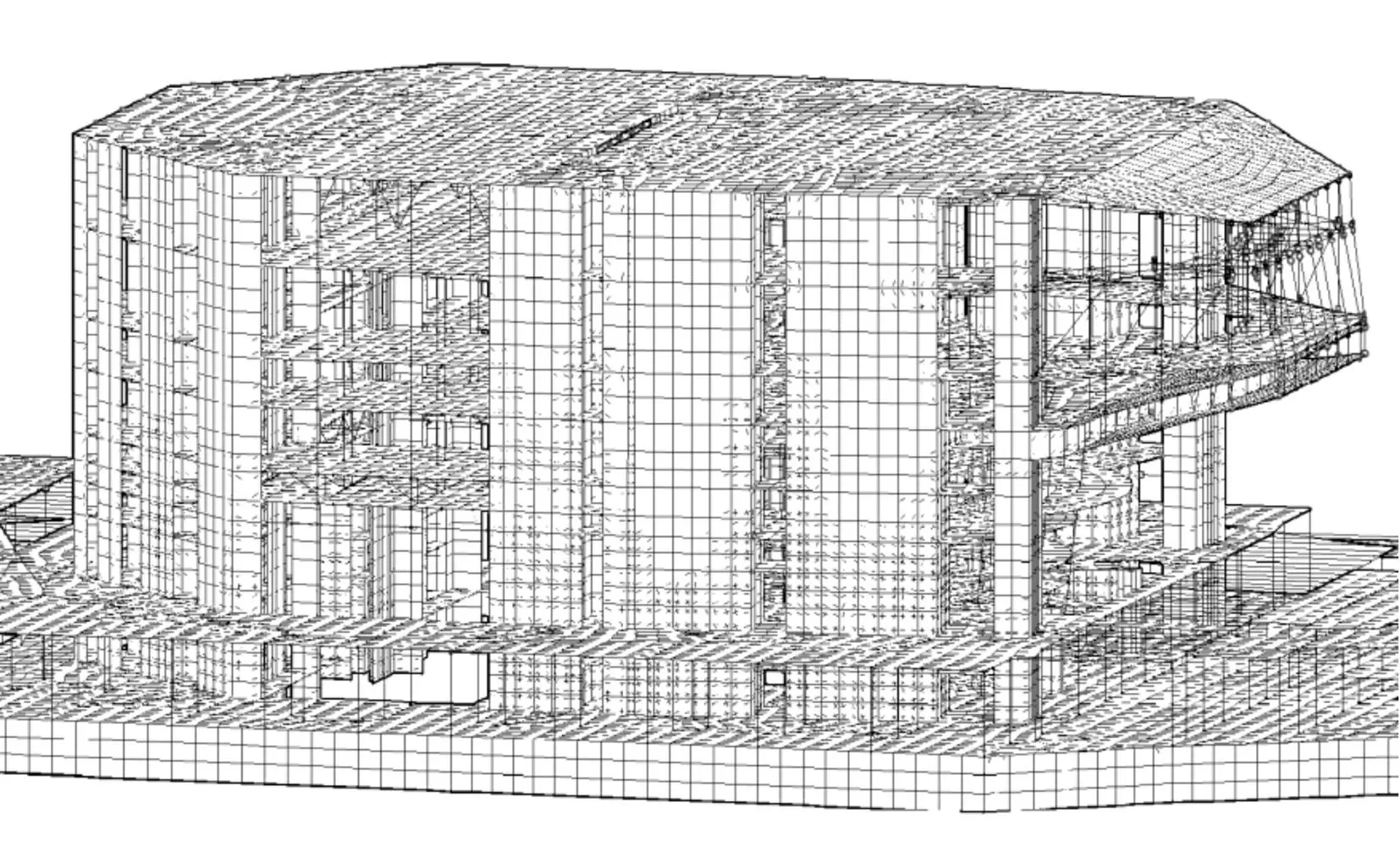
圖17　7度罕遇烈度地震作用下出鉸情況 Fig.17 Damage patterns under the rare earthquake of magnitude of 7

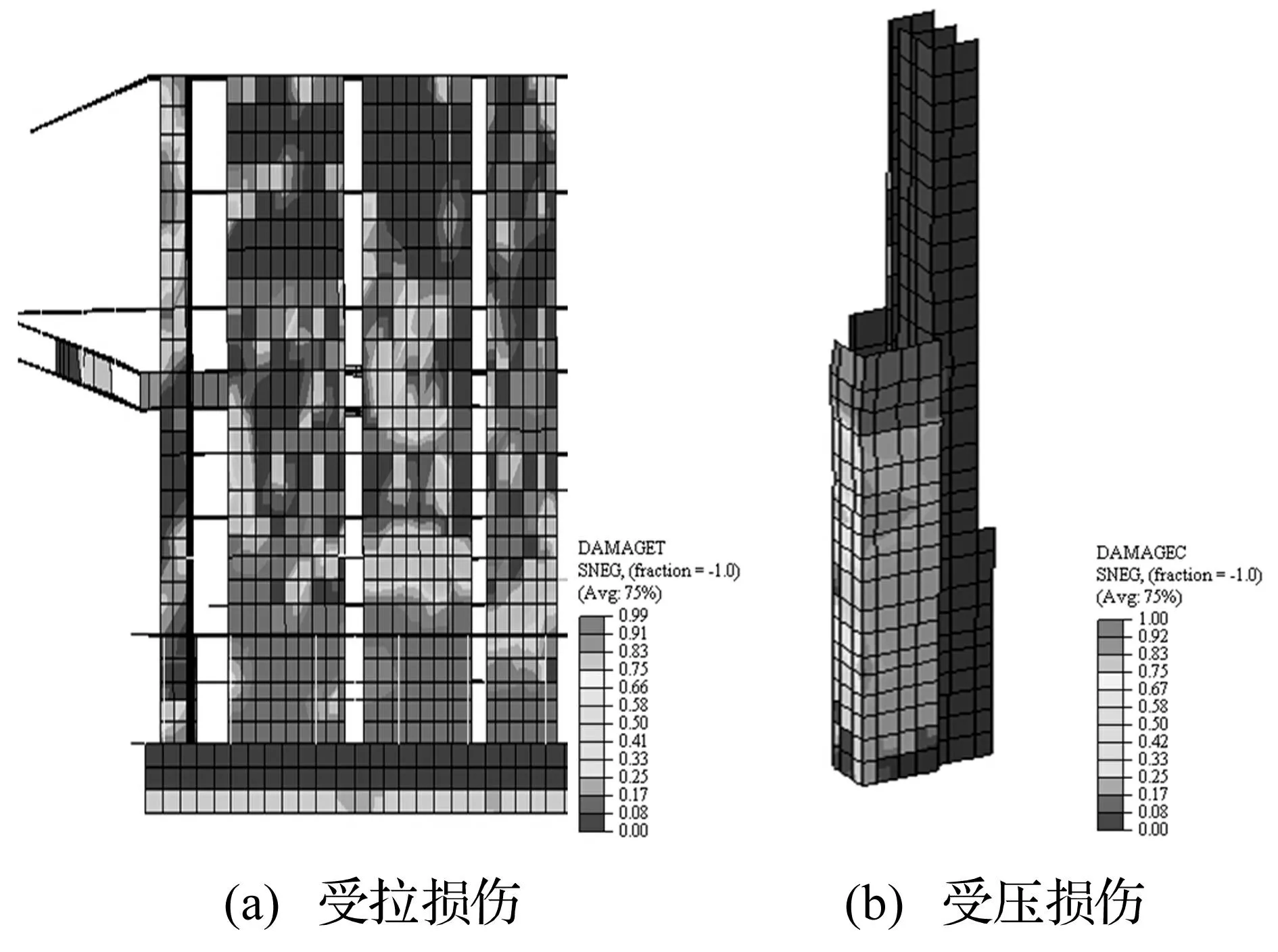
圖18　剪力墻筒體的最終損傷狀態 Fig.18 Final damage nephogram of shear-wall

2.3.4斜柱及斜撐分析

考察在7度EL-centro波罕遇工況下的斜柱應力狀態，在圖19為框架斜柱的軸向應力達到最大時的云圖，可以看出在地震過程中大部分斜柱基本均處于受壓狀態，且位于離對稱中心最近的兩斜柱軸向壓應力最大，柱底軸壓應力達到14.69 MPa，但未達到混凝土的破壞狀態，且該應力值隨著斜柱遠離對稱中心的距離增大而逐漸減小，在端部的兩斜柱出現輕微受拉。可以看出該結構中大部分豎向壓力由結構中的剪力墻筒體來承擔，框架柱在結構中分擔軸力較小，并在整個地震過程中保持安全工作狀態。

圖20為前述梁上斜撐的軸向應力云圖，該圖顯示出斜撐在整個地震輸入的過程中基本保持受壓狀態，受拉應力非常小，且該處斜撐的受力相對附近其他構件的受力較為不利，最大軸向壓應力約為20 MPa，小于所采用混凝土的抗壓強度標準值，并未達到破壞。

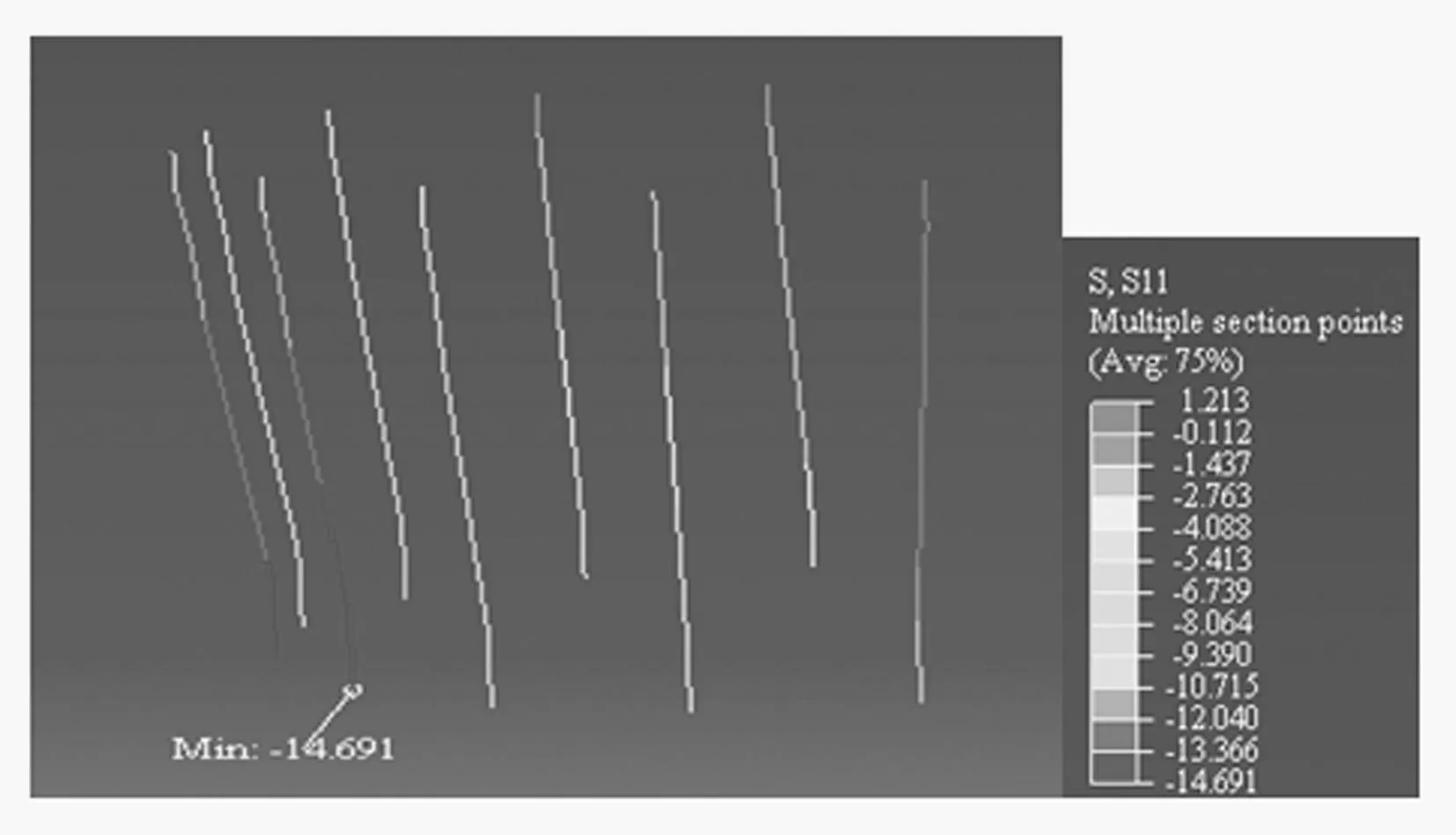
圖19　斜柱應力云圖(單位：MPa) Fig.19 Axial stress nephogram of inclining columns

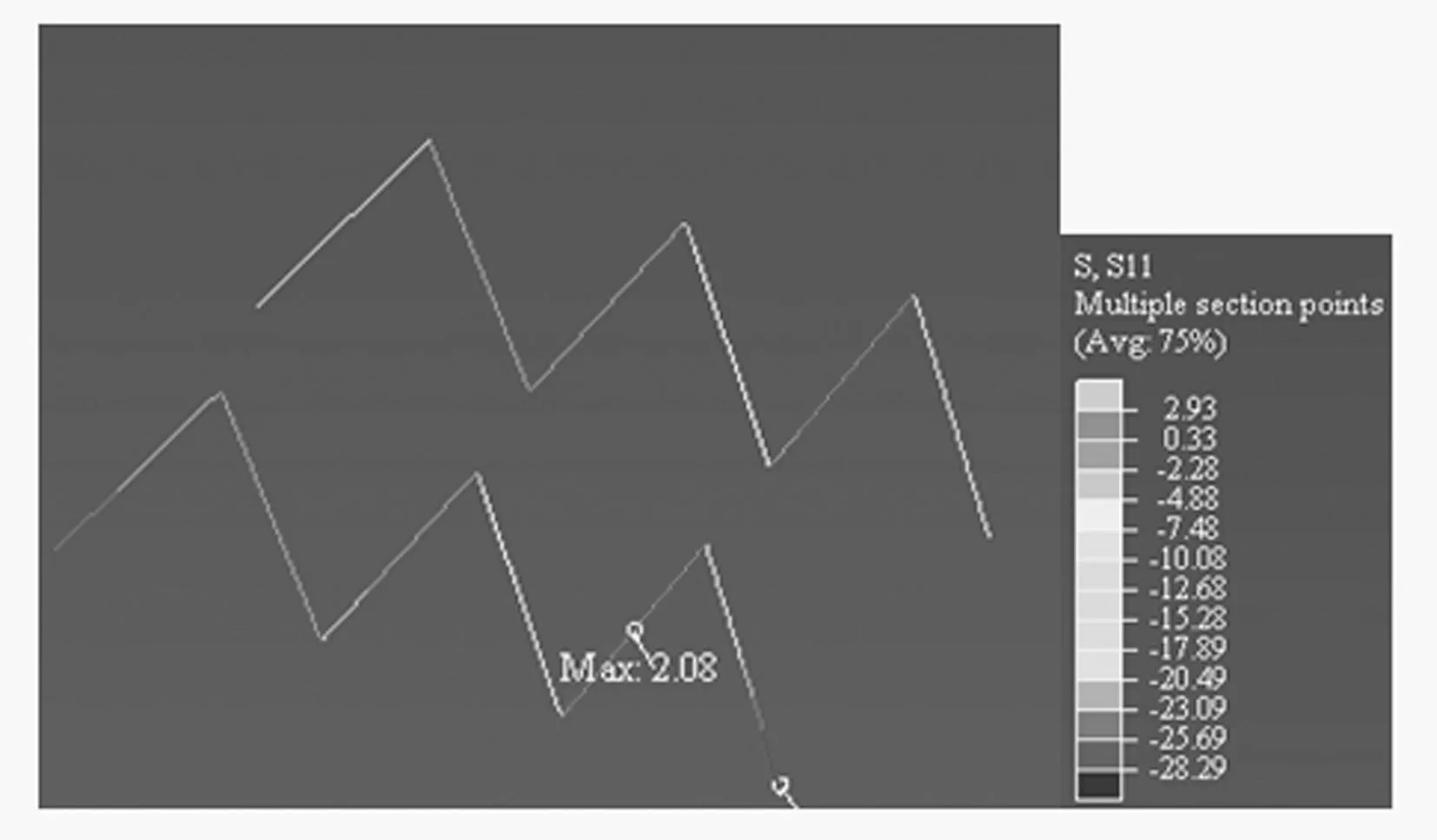
圖20　梁上斜撐軸向應力云圖(單位：MPa) Fig.20 Axial stress nephogram of diagonal brace on the beam

2.4　模型截斷設計

該結構因存在大懸挑、大空間、平面、立面均不規則等特點，擬對該結構進行振動臺模擬地震試驗以評估其抗震性能，但由于原型結構底盤尺寸較大，以及振動臺臺座的尺寸有限，在設計試驗模型時為了盡可能減小其縮尺比例來提高試驗的精度，對底盤裙房非主樓部位進行截斷；現對截斷前后的結構進行動力響應對比，從而來評價此截斷方法的合理性。

2.4.1位移響應

圖21為結構在截斷前后剪力墻N1筒體(見圖1)在三種地震波激勵下的最大樓層位移對比分析圖，從圖中可以看出截斷前后筒體最大樓層位移隨樓層高度的變化趨勢相同，且在結構X向曲線基本重合，在Y方向僅存在較小的數值差別。在結構頂層此差別達到最大：在EL-centro波激勵下頂層最大位移的差別為2.36%(X向)和5.32%(Y向)，在TAFT波激勵下頂層最大位移的差別為4.63%(X向)和9.90%(Y向)。

2.4.2加速度響應

圖22為截斷前后結構在對應7度罕遇地震波激勵下的樓層最大加速度對比圖，由于結構各筒體截斷前后加速度差異基本相同，現僅列出有代表性的靠近懸挑端的筒體N1的對比分析圖，從圖中可以發現樓層的加速度響應峰值基本相同，但結構Y向在標高20.00 m以下存在一定差別，是由于被截斷的裙房對裙房結構樓層以及與裙房相連的主樓結構存在一定的影響。但對裙房頂部標高以上的懸挑樓層影響較小，從而驗證了該截斷方法對于考察結構的大懸挑樓層動力響應的合理性。

2.4.3基底剪力響應

表3為三條地震波7度多遇和罕遇工況下結構截斷前后的基底最大剪力值和剪重比。截斷前后結構的重力荷載代表值分別為1.57×106kN和1.39×106kN，如表中所示，在7度多遇工況中，EL-centro波下的基底剪力響應最大，三條波下結構截斷前后的剪重比均滿足規范中的建議值；在截斷前后基底剪力變化幅度較小，這是由于基底剪力大部分均由剪力墻筒體來承擔，框架相應承擔比重較小，而所截斷的裙房均為框架結構，所以截斷部分承擔的基底剪力對總剪力的影響很小。罕遇地震作用下總基底剪力相對于多遇地震下的剪力有所放大，但對三條地震波激勵下的放大值并不相同，這也表明結構在三條地震波作用下達到的塑性狀態存在著差異。

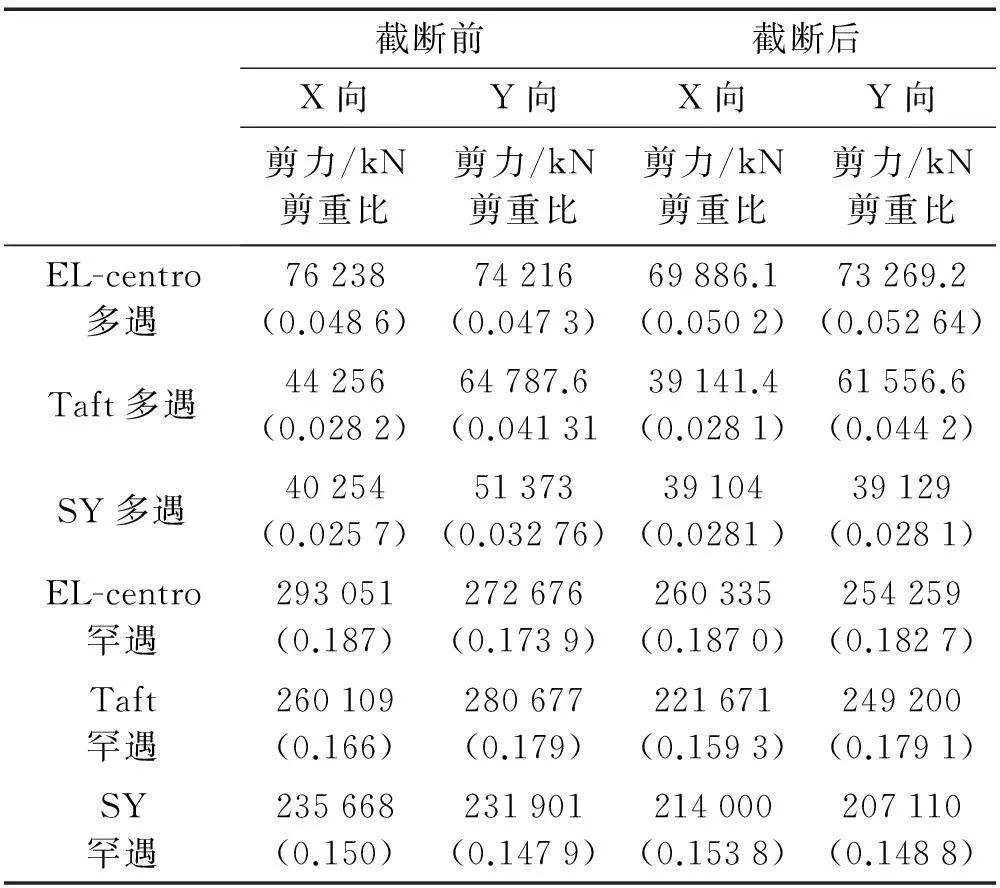
表3　結構基底剪力及剪重比

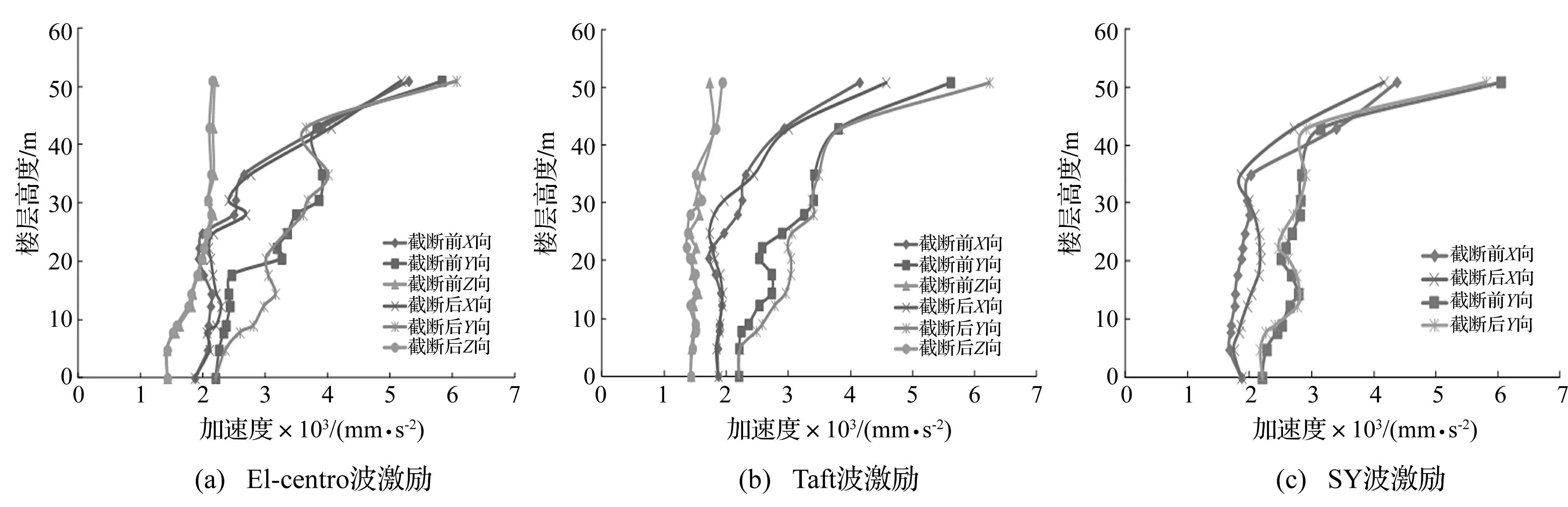
圖22　截斷前后結構樓層加速度對比 Fig.22 Comparison of acceleration before and after cutoff of the podium

2.4.4樓板變形

由于結構中存在大跨度、大懸挑樓板，現對結構頂層樓板變形進行分析，由于Elcentro波下的位移響應較大，取其進行分析：圖23為頂部樓板在7度罕遇EL-centro波激勵下的三向變形云圖，由于在ABAQUS中加速度時程是在解除底部支座某方向約束后施加加速度，所以后處理中的位移云圖需扣除支座位移引起的剛體平動。在圖中時刻X,Y,Z三向的支座位移分別為120.75 mm，174.94 mm，297.11 mm，故樓板在X向的最大位移為26.1 mm，出現在靠近懸挑端的剪力墻筒體區域；在Y向的最大位移為5.213 mm，出現在懸挑端部，這是由于懸挑端在Y方向缺少約束所致；樓板豎向的最大位移分別為35.45 mm(隆起),-127.673 mm(下陷)，可以看出，四周剪力墻區域附近的樓板出現了隆起，而懸挑末端和靠近懸挑端部的大跨區域的樓板均發生了較大的負向位移，這是由于懸挑部位和大跨部位對豎向地震激勵下的響應較為激烈。在結構設計中應考慮增加樓板的平面外剛度以控制樓板的豎向位移。

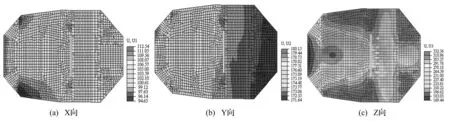
圖23　7度罕遇烈度EL-centro波作用下頂層樓板變形云圖(單位：mm) Fig.23 Floor deformation under rare intensity 7 EL-centro

3振動臺試驗驗證

該結構的模型地震振動臺試驗在同濟大學結構實驗室進行，試驗中采用的相似關系如表4所示；首先根據試驗設備條件和模型概況確定尺寸、強度、加速度三個主要物理量的相似關系，并通過量綱分析方法[12-13]推導出其他參數的相似關系。由于原型結構地下室頂板厚度小于180 mm，不足以作為結構的嵌固端，所以在模型中考慮地下室底板作為嵌固端。由于在上述分析中已驗證截斷裙房的合理性，在試驗中對截斷后的模型進行制作，并對建筑內部的部分樓板開洞進行了規則化處理，忽略對結構性能影響較小的洞口。經簡化后制作完成的試驗模型總高為1.697 m，模型自重為5.54 t，施加配重質量為5.66 t，模型總質量為11.2 t，施工完成后的模型圖如圖24所示。

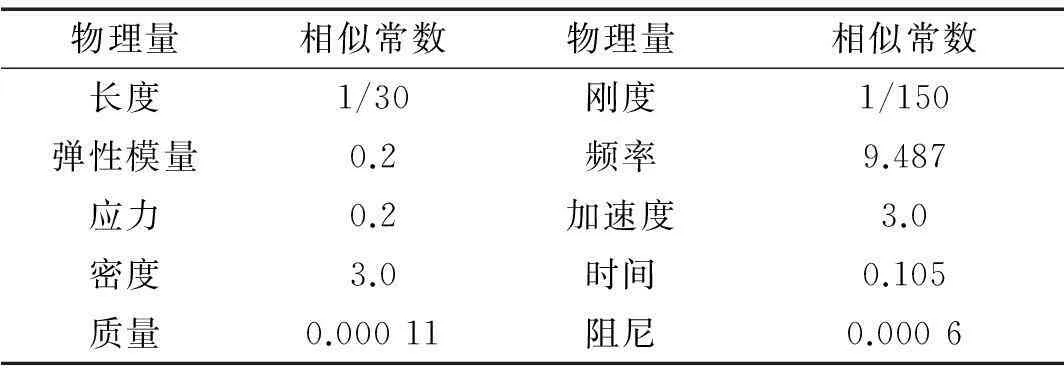
表4　模型相似關系

圖24　試驗模型圖 Fig.24 General view of the model

試驗模型結構中混凝土采用C10微粒混凝土進行模擬，梁柱中鋼筋和樓板中的鋼筋分別采用鍍鋅鐵絲和鐵絲網片進行模擬。

在模型和構件設計中，對正截面承載能力和斜截面承載能力的控制，分別依據抗彎能力等效和抗剪能力等效的原則進行設計。

為了模擬原結構中預應力鋼絞線的作用，試驗模型中采用了直徑為5 mm消除應力鋼絲模擬，錨具采用三孔或五孔的墩頭錨具，預應力的等效原則為有效預應力合力等效。在模型制作過程中，根據微粒混凝土強度較低的特點，在構造措施方面適當加強了預應力筋的張拉端和錨固端。

根據工程所處場地類別和設計地震分組(7度，0.10 g，Ⅱ類場地)選用上述兩條實際強震記錄和人工模擬的加速度時程曲線：①EL-centro天然波；②Taft天然波；③人工地震動SY波。7度設防水準地震作用下臺面激勵按照①~③時程曲線的順序進行輸入[14]，為了避免模型的結構的累積損傷，在中震水準下只輸入較為典型的EL-centro波進行激勵；輸入地震波加速度幅值按照動力相似關系進行放大，持續時間根據時間關系的相似比進行壓縮，三向輸入中的加速度幅值比例為1∶0.85∶0.65，在各水準地震作用前后均對結構進行白噪聲掃頻以或者模型結構動力特性。表5為型結構前3階振型的頻率及對應阻尼比。可以看出，7度罕遇烈度水準地震作用下，結構的頻率有所下降，對應

阻尼比增大，表明結構在7度罕遇烈度地震后已有損傷，7度半罕遇工況結束后，模型前兩階平動的自振頻率分別由試驗開始的19.75 Hz,21 Hz下降到16.75 Hz，18 Hz，阻尼比分別由6.09%和10.19%變化到12.85%，15.82%。根據相似關系推導出原型的前三階周期分別為0.482 s(水平平動),0.454 s(水平平動),0.389 s(水平扭轉),與有限元分析結果存在約15%左右的誤差，這是由于模型結構在施工中樓板無法做到精確等效后的4 mm，采用統一的1 cm板厚，造成模型的整體剛度偏大。

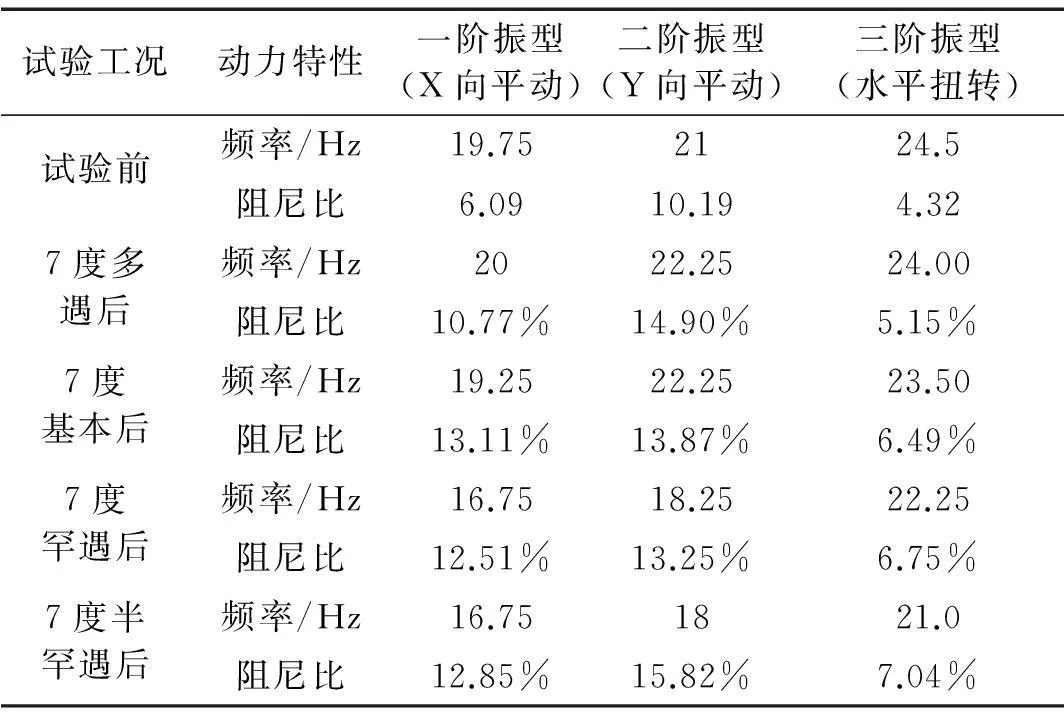
表5　模型動力特性

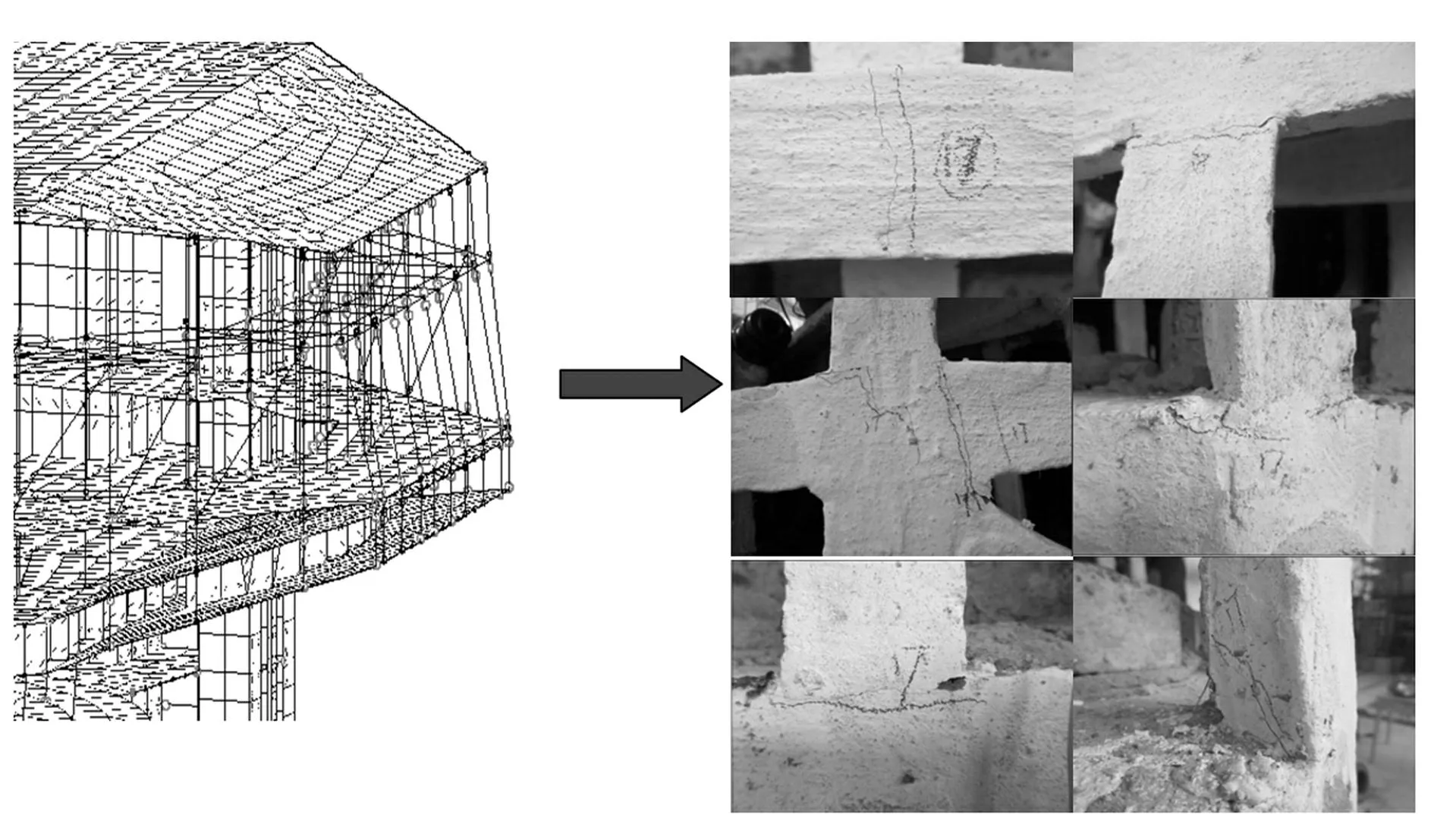
圖25　模型懸挑端破壞形態 Fig.25 Failure pattern of the cantilevered part of the model

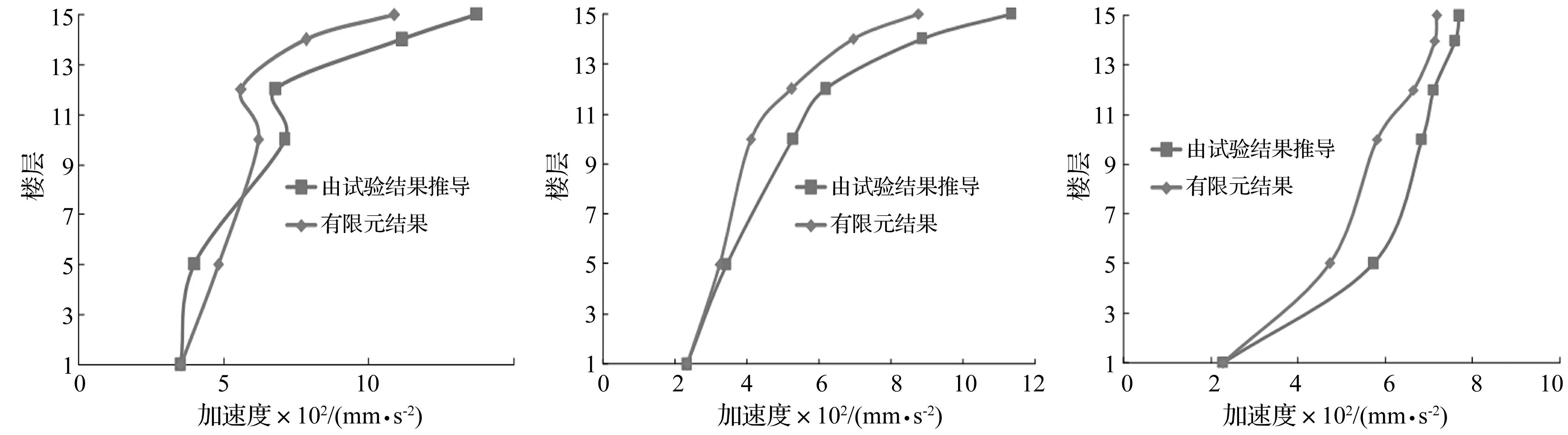
圖26　試驗結果與有限元分析加速度響應對比圖 Fig.26 Comparison of acceleration response

圖25為結構在7度罕遇工況結束后的破壞狀態，主要表現為懸挑端梁柱節點出現裂縫，這與有限元模型中的破壞形態相吻合。再考察彈性狀態下試驗結果和有限元模擬結果的對比情況，以加速度響應為例，圖26為對應7度多遇水準EL-centro波三向激勵下試驗模型結果和有限元計算結果的關鍵樓層加速度響應對比圖，從圖中可以看出兩者趨勢保持一致，僅在數值上存在較小的差別，這也是由于試驗模型剛度偏大、所用材料的參數與理論值存在一定的誤差以及試驗中的系統誤差對結果產生了一定的影響。通過對比可發現模型試驗結果可以與有限元模擬結果相互印證，此外也從模型自振特性、破壞形態、加速度響應等方面也驗證了在有限元分析中所采用計算模型的合理性。

4結論

通過對某大懸挑結構進行彈塑性時程分析，并經大縮尺整體模型模擬地震振動臺試驗，得到以下結論：

(1)結構在所選的7度多遇和7度罕遇抗震設防烈度對應加速度峰值的地震波作用下，最大層間位移角分別為1/1026和1/249，均滿足規范要求。

(2)結構懸挑端部在三向地震激勵下，端部節點水平位移響應基本相同，豎向位移則呈現兩端小，中間大的拱形分布形式。

(3)結構在7度罕遇抗震設防烈度對應的加速度峰值的地震波作用下，結構的塑性鉸主要出現在筒體墻片之間的連梁端部、懸挑部位的梁柱節點部位；結構中的斜柱，梁上斜撐等特殊構件未發生破壞，保持安全工作；剪力墻的受壓損傷較輕，集中出現在內筒體部位，受拉損傷較重，主要集中在底部墻體以及與懸挑部位相鄰的懸挑樓層剪力墻處；懸挑端樓板及頂部大跨部位樓板在豎向地震作用下撓度較大。

(4)對結構的裙房截斷來進行振動臺的模型設計，通過對截斷前后模型的動力響應進行對比，驗證了該設計方法在本試驗中的合理性。結構的振動臺試驗結果與有限元分析結果較好地互相印證，從而可以從多角度來分析結構模型在地震作用下的受力機理和破壞形態。

(5)相同烈度、相同水準的不同地震波作用下的結構各項反應有一定差異，分析中應選用一定數量且合理的地震波。

(6)建議結構設計時對原結構作如下改進：①可適當減小結構整體水平抗側剛度；②對懸挑端預應力梁柱節點重點設計；③加強屋頂大跨區域的樓板平面外剛度以減小豎向地震響應。

參考文獻

[1]徐培福. 復雜高層建筑結構設計[M]. 北京: 中國建筑工業出版社， 2005.

[2]Das S, Nau M.Seisimic design aspects of Vertical irregular reinforced concrete buildings[J]. Earthquake Spectra,2003, 19:455-477.

[3]JGJ 3-2010 高層建筑混凝土結構技術規程[S].北京:中國建筑工業出版社，2010.

[4]GB 50011-2010 建筑抗震設計規范[S].北京:中國建筑工業出版社，2010.

[5]顧祥林，孫飛飛.混凝土結構的計算機仿真[M].上海：同濟大學出版社，2002.

[6]呂西林.復雜高層建筑結構抗震理論與應用[M]. 北京：科學出版社，2007.

[7]呂西林，金國芳，吳曉涵.鋼筋混凝土非線性有限元理論與應用[M].上海：同濟大學出版社，2002.

[8]吳曉涵，呂西林.反復荷載下混凝土剪力墻非線性有限元分析[J].同濟大學學報， 1996,24(2): 117-123.

WU Xiao-han, Lü Xi-lin. Nonlinear finite element analysis of reinforced concrete slit shear wall under cyclic loading[J]. Journal of Tongji University, 1996,24(2): 117-123.

[9]楊溥，李英民，賴明. 結構時程分析法輸入地震波的選擇控制指標[J]. 土木工程學報，2000,6:33-37.

YANG pu, LI Ying-min, LAI Ming. A new method for selecting inputting waves for time-history analysis[J]. China Civil Engineering Journal,2000,6:33-37.

[10]楊紅,任小軍,徐海英. 雙向水平地震下時程分析法中輸入波的選擇[J]. 華南理工大學學報(自然科學版)，2010,11:40-46.

YANG Hong, REN Xiao-jun, XU Hai-ying.Selection of input waves in time-history analysis under bi-direction horizontal seimic action[J]. Journal of South China Univesity of Technology,2010,11:40-46.

[11]肖明葵,劉綱,白紹良. 基于能量反應的地震動輸入選擇方法討論[J]. 世界地震工程，2006,3:89-94.

XIAO Ming-kui, LIU Gang, BAI Shao-liang. Some methods of selecting earthquake wave based on energy response[J]. World Earthquake Engineering, 2006,3:89-94.

[12]姚振剛，劉祖華.結構抗震試驗[M]. 上海:同濟大學出版社，1996.

[13]周穎，盧文勝，呂西林. 模擬地震振動臺模型實用設計方法[J]. 結構工程師，2003, 19(3):30-33.

ZHOU Ying, LU Wen-sheng, LU Xilin, Practical model design method of shaking table tests[J]. Structural Engineers, 2003, 19(3):30-33.

[14]周穎，張翠強，呂西林. 振動臺試驗中地震動選擇及輸入順序研究[J]. 地震工程與工程振動， 2012,32(6): 32-37.

ZHOU Ying, ZHANG Cui-qiang, LU Xi-lin. Method of ground motion selection and input in shaking table tests[J]. Earthquake Engineering and Engineering Vibration, 2012,32(6): 32-37.