靈活選用 簡捷解題

李君

蘇科版八年級上冊第97頁中有這樣一道題：

在△ABC中，∠C=90°.

（1） 已知AC=5，BC=12，求AB;

（2） 已知AC=2，BC=3，求AB;

（3） 已知AB=25，AC=24，求AC.

本題是勾股定理的應用，即可以直接應用勾股定理的表達式a2+b2=c2來解決，但在上述解題過程中，我們應用了它的變式：c= ，b= .很明顯，這樣的解題過程更簡捷.因此，我們在解題時，要注意根據題目的具體特點來選擇勾股定理的表達式及其變式，以優化解題過程.下面舉例說明.

例1 ? 如圖1，矩形ABCD中，AB=3，AD=1，AB在數軸上，若以點A為圓心，對角線AC的長為半徑作弧交數軸的正半軸于M，則點M表示的數是（ ? ? ?）.

【點評】這是在數軸上尋找表示無理數的點，說明數軸上的點與實數是一一對應的，體現了數形結合的思想.

例2 ? 在Rt△ABC中，已知兩邊長分別是5和12，則其周長為________.

【分析】5和12可以是直角邊，也可以是一條斜邊和一條直角邊，分兩種情況用勾股定理表達式的變式求解較簡捷.

解：當5和12為直角邊時，由勾股定理表達式的變式可知，斜邊為 =13，此時Rt△ABC的周長為5+12+13=30;當12為斜邊時，5為直角邊，則由勾股定理表達式的變式可知，另一條直角邊為 ，此時Rt△ABC的周長為5+12+ .綜上，周長為30或17+ .

【點評】已知直角三角形兩邊長求第三邊，要注意分兩種情況思考：一是這兩邊為直角邊，二是這兩邊中較大邊為斜邊，較小邊為直角邊，要謹防漏解.

例3 ? （2015·江蘇泰州）如圖2，矩形ABCD中，AB=8，BC=6，P為AD上一點，將△ABP沿BP翻折至△EBP，PE與CD相交于點O，且OE=OD，則AP的長為_______.

【分析】設BE交CD于點G，由折疊的性質可知EP=AP，∠E=∠A=90°，BE=AB=8，由ASA可證明△ODP≌△OEG，得出OP=OG，PD=GE，設AP=EP=x，則PD=GE=6-x，DG=x，求出CG、BG，再由勾股定理的表達式列方程求解較簡捷.

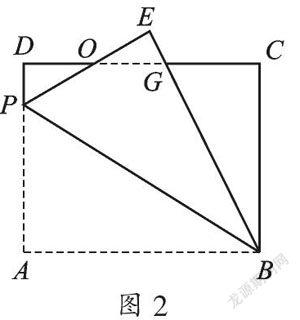
解：∵四邊形ABCD是矩形，∴∠D=∠A=∠C=90°，AD=BC=6，CD=AB=8，根據題意得△ABP≌△EBP，∴EP=AP，∠E=∠A=90°，BE=AB=8，又△ODP≌△OEG（ASA），∴OP=OG，PD=GE，∴DG=EP，設AP=EP=x，則PD=GE=6-x，DG=x，∴CG=8-x，BG=8-（6-x）=2+x，根據勾股定理得：BC2+CG2=BG2，即62+（8-x）2=（x+2）2，解得：x=4.8，∴AP=4.8.

【點評】熟練掌握翻折變換和矩形（長方形）的性質，借助AP=x，并用x表示出其他未知量，再利用勾股定理列出方程是解決問題的關鍵.

（作者單位：江蘇省興化市楚水初級中學）