知錯能改,善莫大焉
薛麗萍
勾股定理是幾何的一個基本定理,是解決幾何問題的重要工具之一,也是體現數形結合思想的紐帶.同學們在學習勾股定理時,往往會有一些錯誤的認識.現在我們一起來整理勾股定理易錯題型,找出錯因,在糾錯中學習勾股定理.
一、 定理理解不透徹,定勢思維來影響
同學們在勾股定理的理解上,往往會受思維定勢的影響,不認真審題,忽略其關鍵點,草率出手而出錯.
例1 ? 已知某直角三角形的三邊分別是3、4、x,則x2的值為_______.
【錯因分析】3、4、5是同學們最先接觸、印象最深的一組勾股數,當看到直角三角形兩邊是3和4時,受思維定勢的影響,自然而然地認為第三邊一定是5,故x2的值為25.實際上,在直角三角形中沒有明確哪邊是斜邊時,應分類討論考慮全面.
【正解】3不可能作為斜邊;當4是斜邊時,x2=7;當x是斜邊時,x2=25.故x2=7或25.
【感悟】勾股定理很容易,其中一角是直角;應用注意三條邊,分清哪條是斜邊;直角邊要平方和,斜邊平方等于它.
二、 一目十行,錯加條件留遺憾
數學解題時看到熟悉的圖形,很多同學往往粗略審題,忽略了題目的條件和與熟悉的圖形的細微差別,把未知的結論當已知條件直接使用,導致錯解.
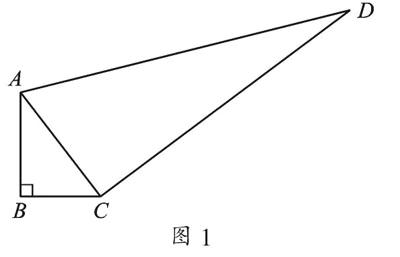
例2 ? 如圖1,在四邊形ABCD中,∠B=90°,AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,試求四邊形ABCD的面積.
【錯因分析】同學們在解決此題時,往往會有這樣的疑惑:我的答案是正確的,為什么不得分呢?那是因為本題中只知△ABC是直角三角形,大多數同學錯誤地理解為△ACD也是直角三角形,直接利用直角三角形的面積公式求解.而實際上△ACD的形狀需要根據其三邊長度之間的數量關系,利用勾股定理的逆定理作出判斷.
【正解】在Rt△ABC中,由勾股定理求得AC=5 cm,∵AC2+CD2=AD2,∴△ACD是直角三角形,且∠ACD是直角,∴四邊形ABCD的面積=4×3+×5×12=36.
【感悟】解題不能憑經驗,審清題意多留心,要證直角有方法,勾股定理逆定理!
三、 根據條件來作圖,考慮全面防漏解
在數學學習中,同學們處理常見的圖形和條件時,往往容易忽視非常規圖形,造成漏解,甚至解答錯誤.我們應排除定向思維產生的錯解,周密地考慮問題,用分類討論的思想方法來解決此類問題.
例3 ? 在△ABC中,AB=15,AC=20,BC邊上的高AD=12,求BC的長.
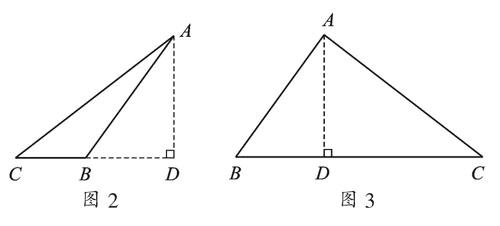
【錯因分析】本題沒有直接給出符合條件的示意圖,需要同學們先根據題意畫出符合要求的圖形再解答.在作出示意圖分析問題時,我們往往習慣性地將△ABC理解成銳角三角形,沒有全面判斷三角形的形狀,出現漏解情況.在畫示意圖的過程中,我們要根據條件,考慮所作點或線的呈現順序,如第一步由AB=15可確定線段AB,第二步由AC=20確定點C時,要考慮點C的位置.當位于AB的左側,形成的∠ABC為鈍角,如圖2;當位于AB的右側,形成的∠ABC為銳角,如圖3.
【正解】如圖2,當∠ABC為鈍角時,在Rt△ACD和Rt△ABD中,由勾股定理得CD2=AC2-AD2=256,BD2=AB2-AD2=81,∴CD=16,BD=9,故BC=7;如圖3,當∠ABC為銳角時,可求得BC=25.
【感悟】在勾股定理的學習中,要養成良好的審題習慣,重視知識的呈現過程,運用分類討論思想,突破思維定勢,避免漏解.
四、 直覺經驗有誤區,嚴謹計算現事實
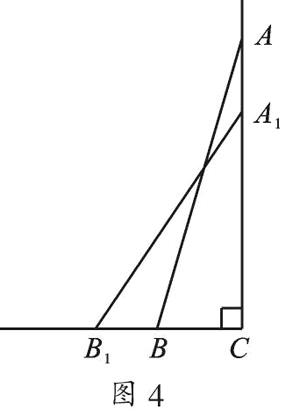
例4 ? 如圖4,一架長2.5米的梯子AB,斜靠在豎直的墻AC上,梯子的底部B到墻底端C的距離為0.7米,如果梯子的頂端沿墻下滑0.4米,那么梯子的底端也將向外移0.4米嗎?
【錯因分析】同學們沒有通過嚴謹的思考與計算,憑直覺會認為如果梯子的頂端沿墻下滑0.4米,而梯子的長度是不變的,那么梯子的底端肯定也要向外移0.4米.事實上,直覺往往會產生錯誤,我們需要運用數學知識,通過計算B1B的長度來判斷梯子的底端移動的距離.
【正解】在Rt△ABC中,由勾股定理得AC=2.4,∴A1C=2,Rt△A1B1C中,由勾股定理得B1C=1.5,∴B1B=0.8,∴梯子的底端應向外移0.8米.
【感悟】看似簡單的實際問題,不能光憑直覺,只有轉化為數學問題,利用勾股定理計算線段長度,才能呈現事實真相.
剖析解數學題的易錯點,對于培養數學的思維品質,提高解題能力具有重要意義,讓我們知錯能改,輕松應對勾股定理!
(作者單位:江蘇省常州市武進區湖塘實驗中學)

