聯(lián)手方程解難題

張萍

勾股定理是用代數(shù)思想解決幾何問題的重要工具，方程是解決數(shù)學問題的另一重要工具，兩者的有機結(jié)合，能輕松解決許多數(shù)學問題.下面，我們依舊利用前文中引用的教材例題，深入探討如何將勾股定理和方程聯(lián)手解題.

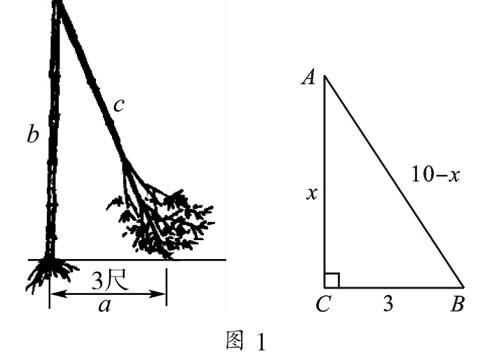
原題 ? （蘇科版教材八上第86頁例1）《九章算術(shù)》中有一道“折竹”問題：“今有竹高一丈，末折抵地，去本三尺，問折者高幾何？”題意是：一根竹子原高1丈（1丈=10尺），中部有一處折斷，竹梢觸地面處離竹根3尺，試問折斷處離地面多高？

【點評】勾股定理本身就是一個關于直角三角形三邊長的數(shù)學等式，我們又知道含有未知數(shù)的等式就是方程，故如果用變量表示出直角三角形邊長的話，就可利用勾股定理列出該變量的方程，從而解決相應問題.

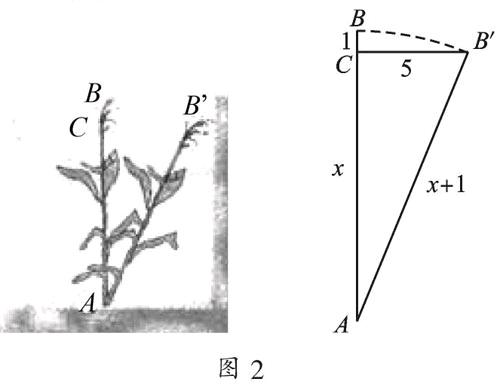
應用一：《九章算術(shù)》中有一道“引葭赴岸”問題：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，適與岸齊.問水深、葭長各幾何？”題意是：有一個池塘，寬10尺，一棵蘆葦生長在它的中央，高出水面1尺.如果把該蘆葦沿水池邊垂直的方向拉向岸邊，那么蘆葦?shù)捻敳壳『门龅桨哆?水深和蘆葦長各多少尺？

【分析】我們可以將其轉(zhuǎn)化為幾何圖形，如圖2所示，根據(jù)題意，可知B′C=5尺，可設水深AC=x尺，表示出蘆葦長AB′=（x+1）尺，根據(jù)勾股定理建立方程，求出方程的解，即可得到水深和蘆葦長.

解：設水深為x尺，則蘆葦長為（x+1）尺.由勾股定理得x2+52=（x+1）2，解得x=12，所以水深12尺，蘆葦長13尺.

【點評】利用勾股定理解決生活中的實際問題，重要的是將實際問題轉(zhuǎn)化成數(shù)學模型（直角三角形模型），將實際問題轉(zhuǎn)化為定理中的“形”，再轉(zhuǎn)化為“數(shù)”.當已知直角三角形一邊長度以及另外兩邊間的關系時，可根據(jù)兩邊間關系設出未知量，從而表示出兩邊，再由勾股定理列方程求解.

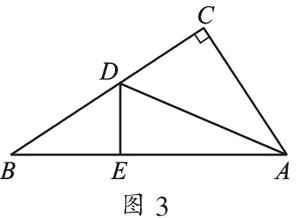
應用二：如圖3，有一張直角三角形紙片ABC，兩直角邊AC=6 cm，BC=8 cm，現(xiàn)將直角邊AC沿直線AD折疊，使它落在斜邊AB上，且與AE重合，你能求出CD的長嗎？

【分析】由折疊的性質(zhì)知CD=DE，AC=AE.根據(jù)題意，在Rt△BDE中運用勾股定理列方程，從而求出DE.

解：設CD=x cm，由題意知DE=x cm，

BD=（8-x） cm，AE=AC=6 cm.

在Rt△ABC中，由勾股定理得：

AB2=AC2+BC2=100 cm2，所以AB=10 cm，

于是BE=10-6=4 cm.

在Rt△BDE中，由勾股定理得：42+x2=（8-x）2，解得x=3.

所以CD的長為3 cm.

【點評】本題有兩個難點，一是折疊前后的三角形之間對應邊的轉(zhuǎn)化，二是在Rt△BDE中用勾股定理時必須用方程思想，勾股定理聯(lián)手方程在折疊問題中有廣泛的應用.

變式 ? 如圖4，在矩形ABCD中，AB=8，BC=4，將矩形沿對角線AC折疊，點D落在D′處，求重疊部分△AFC的面積.

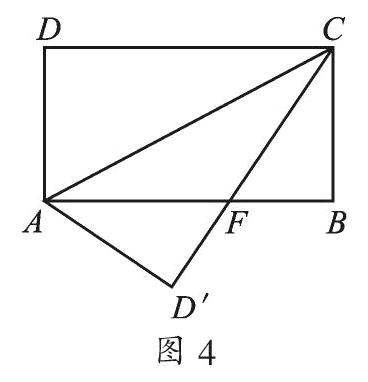
【分析】矩形翻折后易知AF=FC，利用直角三角形BFC，用勾股定理求出CF的長，也就是AF的長，繼而利用三角形面積公式求△AFC的面積.

解：設AF=x，

根據(jù)題意，矩形沿對角線AC對折后有，

∠D′=∠B=90°，∠AFD′=∠CFB，BC=AD′，

∴△AD′F≌△CBF，

∴CF=AF=x，∴BF=8-x，

在Rt△BCF中有：BC2+BF2=FC2，

即42+（8-x）2=x2，

解得：x=5.

【點評】折疊問題是中考中常出現(xiàn)的問題，可鎖定一個直角三角形，找出折疊前后相等的量，再設出未知量，表示出三邊，勾股定理與方程再度完美聯(lián)手.

應用三：如圖5，△ABC中，AB=13，AC=15，BC=14，求△ABC的面積.

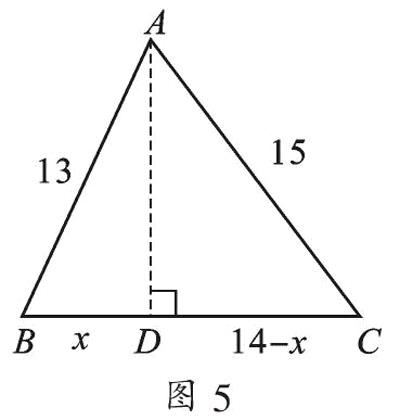
【分析】要求△ABC的面積，可過點A作BC邊上的高，那么就有兩個直角三角形△ABD和△ACD，AD是這兩個直角三角形的公共邊，可設BD長為x，分別在△ABD和△ACD中用勾股定理表示出AD的長，列出方程，求得BD的長，再根據(jù)勾股定理求得AD的長，從而求出三角形的面積.

解：作BC邊上的高AD.

設BD=x，則CD=14-x.

在Rt△ABD中，由勾股定理得，

AD2=AB2-BD2=132-x2.

在Rt△ACD中，由勾股定理得，

AD2=AC2-CD2=152-（14-x）2，

可得132-x2=152-（14-x）2，解得x=5，

則AD2=132-x2=144，所以AD=12

【點評】△ABC不是一個直角三角形，求三角形的面積就要先求出三角形的高，而高可以把這個三角形分成兩個直角三角形.兩個三角形中都有兩個未知量，并且未知量不能用同一個未知數(shù)表示，所以必須兩次應用勾股定理列出兩個關系式，從而求得三角形的高和面積.解決本題的關鍵是利用兩個直角三角形的公共邊建立方程.

方程思想是數(shù)學中的一種重要思想，而勾股定理反映的直角三角形三邊的關系正是構(gòu)建方程的基礎，故與勾股定理有關的許多問題的解決都要跟方程相組合.所以我們在平時的學習過程中，要注重培養(yǎng)這方面的技能、思想.

（作者單位：江蘇省常州市蘭陵中學）