函數的間斷點及其分類

黃玉蘭

摘 ?要：本文通過舉例的形式介紹了間斷點的不同類型，用圖表歸納的形式對間斷點的分類進行了總結，并分情況概況了判斷初等函數和分段函數間斷點及其分類的方法步驟。

關鍵詞：間斷點;分類;判斷方法

由函數的定義可知，引發函數在某點間斷的原因有多種，如何判斷函數間斷點的類型是學生學習的一個重點和難點，本文通過例題并結合圖形介紹間斷點的分類，并用歸納總結的方式對間斷點的分類和如何判斷間斷點進行了介紹。

一、函數間斷點的定義

根據函數在連續的定義，函數f（x）在x=x0處連續需滿足三個條件：（1）f（x）在x0及其領域有定義。（2） f（x）存在。（3）

f（x）=f（x0）。上述條件中，若至少有一個不滿足，則稱f（x）在x0處間斷，即不連續;為的間斷點。由函數的定義可知，引發函數在某點間斷的原因有多種，如何判斷函數間斷點的類型是學習的一個重點和難點，接下來結合圖形介紹間斷點的分類，并歸納總結如何判斷間斷點的方法.

二、間斷點的分類

造成函數f（x）在x0處間斷的原因有多種，由于 f（x）存在的充要條件是f（x0+0）、f（x0-0）都存在且相等，下面通過舉例從左右極限的角度出發對間斷點進行分類：

例1、 討論函數 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 在x=0處的連續性

分析：函數圖像如下圖1所示

圖1

解：在x=1處：f（1+0）=f（1-0）=1，左右極限都存在而且相等，可知 f（x）=1，但f（1）=1≠ f（x）=1，所以x=1為函數的間斷點。

左右極限都存在且相等的間斷點稱為可去間斷點.可去間斷點在圖形上的特點是：相當于連續的曲線去掉了這一點，或者說只要定義這點的函數值等于極限值，則函數在該點連續。

例2、 討論函數 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?在x=1處的連續性

分析：函數圖形如下圖2所示

圖2

解：在x=1處：f（1+0）=2，f（1-0）=1左右極限都存但是不相等，可知 f（x）=1不存在，所以為函數的間斷點。左右極限都存在但不相等的間斷點稱為跳躍間斷點.跳躍間斷點在圖形上的特點是：由于左右極限存在但是不相等，曲線軌跡在這點發生了一個跳躍性的改變。可去間斷點和跳躍間斷點的共同特點是左右極限都存在，這兩類間斷點統稱為第一類間斷點。相對應的，若左右極限至少有一個不存在的間斷點統稱為第二類間斷點，在第二類間斷點里，我們來熟悉一下以下兩種間斷點：

例3、 分析函數f（x） 的連續性。解：函數在x=0處沒有定義，所以x=0為函數的間斷點，在x=0處 f（x）=∞，可知x=0為第二類間斷點。在數學上我們把極限為無窮大的間斷點稱為無窮間斷點。

例4、 分析函數f（x）sin 的連續性。解：函數在x=0處沒有定義，所以x=0為函數的間斷點，在x=0處左右極限都不存在，可知x=0為第二類間斷點.當趨近于0時，函數在-1和1之間取值，這樣的間斷點稱為振蕩間斷點

無窮間斷點和振蕩間斷點都屬于第二類間斷點.

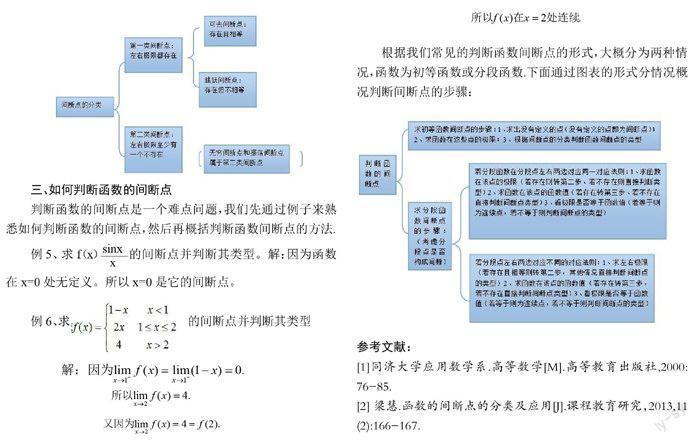
便于理解和記憶，間斷點的分類概括如下：

三、如何判斷函數的間斷點

判斷函數的間斷點是一個難點問題，我們先通過例子來熟悉如何判斷函數的間斷點，然后再概括判斷函數間斷點的方法.

例5、 求f（x） 的間斷點并判斷其類型。解：因為函數在x=0處無定義。所以x=0是它的間斷點。

例6、求 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?的間斷點并判斷其類型

根據我們常見的判斷函數間斷點的形式，大概分為兩種情況，函數為初等函數或分段函數.下面通過圖表的形式分情況概況判斷間斷點的步驟：

參考文獻：

[1]同濟大學應用數學系.高等數學[M].高等教育出版社，2000：76-85.

[2] 梁慧.函數的間斷點的分類及應用[J].課程教育研究，2013，11（2）：166-167.