工科矩陣分析課程教學(xué)實踐與探討

路利軍+曹麗娜

摘要：矩陣分析是數(shù)學(xué)的一個重要分支，理論嚴謹、方法獨特，可以培養(yǎng)學(xué)生的抽象思維能力、邏輯論證能力和理論的實際應(yīng)用能力。本文考慮到專業(yè)發(fā)展的需要，調(diào)整了教學(xué)模式、教學(xué)手段和課堂教學(xué)方式，以期能激發(fā)學(xué)生學(xué)習(xí)熱情，提高當(dāng)前教學(xué)效果，實現(xiàn)教學(xué)相長。

關(guān)鍵詞：矩陣分析;教學(xué)模式;教學(xué)手段;課堂教學(xué)形式

中圖分類號：G642.41 ? ? 文獻標志碼：A ? ? 文章編號：1674-9324（2015）23-0146-02

一、引言

目前，作為大學(xué)數(shù)學(xué)重要分支的“矩陣分析”，其理論和方法表達簡潔、刻畫透徹，是工科必須掌握的數(shù)學(xué)理論之一。所以，許多高校都將其設(shè)置為高年級本科生或研究生的公共基礎(chǔ)課程。然而，“矩陣分析”本身是一門發(fā)展完善、理論嚴謹、方法獨特的基礎(chǔ)課，目前工科矩陣分析理論性太強，過分強調(diào)抽象思維能力，而忽略工程應(yīng)用介紹，使學(xué)生難以理解，在教學(xué)中很難激發(fā)學(xué)生興趣。矩陣公式推演和邏輯證明——抽象的符號表達并進行相應(yīng)的“運算”，讓學(xué)生感到這一切像是在玩數(shù)字游戲，很多時候甚至無法理解所遵循的游戲規(guī)則。任課教師也常常感到學(xué)生數(shù)學(xué)功底不夠厚實，不會靈活地利用所學(xué)過的知識理解遇到的問題，聯(lián)系實際解決問題的能力更是薄弱。這些問題的突出存在，不僅影響了后續(xù)課程的學(xué)習(xí)，也不利于高素質(zhì)創(chuàng)新型人才的培養(yǎng)。因此，考慮到專業(yè)發(fā)展的需要，筆者調(diào)整了教學(xué)模式、教學(xué)手段和教學(xué)方式并且注重工程應(yīng)用，激發(fā)學(xué)生對于矩陣分析課程的興趣，希望能提高當(dāng)前的教學(xué)質(zhì)量，實現(xiàn)教學(xué)相長。

二、積極調(diào)整教學(xué)模式

在現(xiàn)代教學(xué)中，比較有代表性的教學(xué)模式是“傳授—接受”模式。教師講解定量、推導(dǎo)公式，學(xué)生被動地聽講，無暇顧及整體并進行思考。直接后果就是，學(xué)有余力的同學(xué)會浪費寶貴的課堂時間;而學(xué)習(xí)能力較弱的同學(xué)則無法緊隨教學(xué)進度。這樣很難激發(fā)學(xué)生的學(xué)習(xí)興趣，教學(xué)效率也不高，也影響整體教學(xué)效果。宋代理學(xué)家程頤總結(jié)孔子的教育思想時就已經(jīng)指出：孔子教人，各因其材。儒學(xué)集大成者朱熹，一生為學(xué)，窮理及致其知，反躬以踐其實，更明確地指出：圣賢施教，各因其材;小以成小，大以成大，無棄人也。于是，人們應(yīng)考慮分層次教學(xué)，可以制定根據(jù)學(xué)生低年級時對高等數(shù)學(xué)和線性代數(shù)的掌握程度結(jié)合興趣愛好和專業(yè)特點，制定一個標準，大致分成A、B和C三個等級，分別制定不同的教學(xué)進度計劃、教學(xué)內(nèi)容、教學(xué)目標和學(xué)時數(shù)。這樣，對于自學(xué)能力強的A班同學(xué)，基礎(chǔ)知識可以給予更深、更廣的講解。同時，引導(dǎo)同學(xué)們接觸實踐教學(xué)環(huán)節(jié)，培養(yǎng)其運用所學(xué)知識分析和解決實際問題的能力，在這個過程中，如果能發(fā)現(xiàn)問題，建立模型并較為準確地解決該問題，潛移默化中學(xué)生就發(fā)生了質(zhì)的飛躍。而對于C班學(xué)生，可以適當(dāng)放慢教學(xué)進度，降低教學(xué)要求，在基本知識掌握之后鼓勵其多學(xué)習(xí)一些計算軟件，比如Matlab、Mathematics等，在應(yīng)用軟件的過程中，領(lǐng)會所學(xué)知識點，并初步具有一定的基本技能。

三、有效改進教學(xué)手段

在矩陣分析的教學(xué)過程中，最大的忌諱莫過于照本宣科，這樣做學(xué)生們無法體會所學(xué)知識的本質(zhì)。但是，一本教科書、一支粉筆和一塊黑板的傳統(tǒng)教學(xué)手段非常適合重點、難點內(nèi)容的“精講”和“細講”。一次好課，教師通過啟發(fā)與講授，循序漸進，將重點和難點講透、講到點子上、講到要害處，不僅能夠使學(xué)生抓住問題的本質(zhì)、得到要領(lǐng)，而且能夠引發(fā)學(xué)生進一步的思考和聯(lián)想，從而提高學(xué)生的創(chuàng)新思維能力。教師可以將一些板書難于表達、學(xué)生難于理解和接受的復(fù)雜和抽象的內(nèi)容通過多媒體演示。如在講解“矩陣分解”時，可以將矩陣分解的幾何意義結(jié)合起來。這樣，教師不僅在有限的時間內(nèi)傳達了較多的信息，提高了課堂的教學(xué)效率，而且激發(fā)了學(xué)生學(xué)習(xí)的熱情。然而，現(xiàn)代化教學(xué)手段的使用對于培養(yǎng)學(xué)生的技能及思維能力有其不足。因此，傳統(tǒng)教學(xué)手段與現(xiàn)代化教學(xué)手段各有優(yōu)點和不足，我們將二者結(jié)合，根據(jù)教學(xué)的目標和授課的任務(wù)，對于特定的內(nèi)容，分別側(cè)重使用現(xiàn)代化教學(xué)手段或傳統(tǒng)教學(xué)手段。傳統(tǒng)板書與現(xiàn)代多媒體結(jié)合，交相輝映，突出教學(xué)的重點。

四、合理安排課堂教學(xué)組織模式

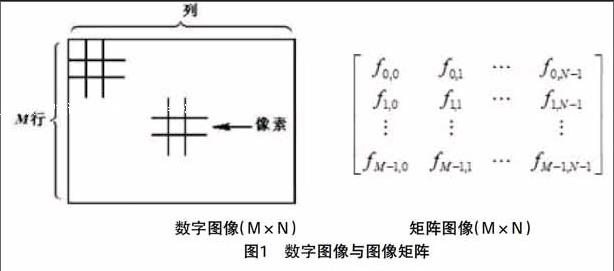
1.以問題切入知識點。一個矩陣可以表示一幅數(shù)字圖像，因此數(shù)字圖像可以采用矩陣分析理論及相應(yīng)算法進行分析。最為直觀的例子是一幅灰度圖像，如圖1所示。矩陣中的每一個單一元素即對應(yīng)于數(shù)字圖像的像素，矩陣元素的值表示該像素點的灰度值，一般取值在[0，255]。顯然，這是一個M×N的矩陣，成像模型可以表示成一個線性方程組：

f=Hu+ε （1）

式中，f、u、ε∈R■（L=M×N是圖像像素點個數(shù)）分別是觀測數(shù)據(jù)、原始圖像和加性噪聲（按列展開得到的向量）;H是退化因子。

數(shù)字圖像處理中最廣泛的圖像重建問題就是已知觀察數(shù)據(jù)f，根據(jù)式（1）估計出圖像u，及求解方程組（1）的問題。顯然，這是一個直接的矩陣計算問題。比如：方程（1）通常是一個病態(tài)問題，因此在求解時就必須考慮方程組的“病態(tài)性”問題，涉及到矩陣分析中矩陣的擾動性分析、主成分分析等;其次在求解病態(tài)方程時，涉及到最小二乘法的求解問題等相關(guān)內(nèi)容;更深入地需要考慮病態(tài)方程的解的唯一性、穩(wěn)定性，又涉及到矩陣分析中廣義逆等。

2.理論分析后給出實例。給定一個矩陣M是一個m×n階矩陣，其全部元素屬于域K，即實數(shù)域或復(fù)數(shù)域。這樣，則有如下分解：

M=UΣV*

其中Σ表示半正定的m×n階對角矩陣;U表示m×n階酉矩陣;而V*表示V的共軛轉(zhuǎn)置，同樣也是n×n階酉矩陣。此分解我們稱作M的奇異值分解。M的奇異值就是Σ對角線上的元素Σi，i。最廣泛采用的方法是奇異值由大而小進行排列。這樣Σ便能由矩陣M唯一確定了。（盡管U和V仍然不能確定。）為了讓學(xué)生明確奇異值分解的意義，可以拿一實例圖像壓縮問題示范。假定一幅圖像有n×n個像素點，一起傳送時整個矩陣的維數(shù)太高，數(shù)據(jù)太大。因此，傳輸要求只傳送比較少的數(shù)據(jù)，在接受終端利用比較少的數(shù)據(jù)重構(gòu)復(fù)原圖像。在此種思路下，如果用n×n矩陣M表示要傳送的n×n個像素。那么對矩陣M首先采用奇異值分解，即得到M=UΣV*，奇異值按照由大到小排序，若從中選擇k個最大的奇異值以及與之相對應(yīng)的左、右奇異向量逼近原圖像，這時，共用了k（2n+1）個數(shù)值代替原來的n×n個圖像像素數(shù)據(jù)。這k（2n+1）個被選擇的新數(shù)據(jù)是矩陣M的前k個奇異值、左奇異向量矩陣U的前k行和右奇異向量矩陣V*的前k列的元素。顯然，對于絕大多數(shù)圖像，通常含有較多的小奇異值時，采用此種方法可以極大降低傳輸量。

五、結(jié)語

矩陣分析教學(xué)過程中涉及到的方面非常多，而具體到每個方面都需要進行深入研究。它在數(shù)字圖像處理及信號分析等工程應(yīng)用中發(fā)揮著極其重要的作用。我們的目標是提高教學(xué)質(zhì)量，使學(xué)生積極主動地掌握本專業(yè)所需的矩陣分析方法，同時培養(yǎng)學(xué)生邏輯能力、推理能力，學(xué)到一種理性的思維模式，以及獨立獲取知識的能力。

參考文獻：

[1]張寶環(huán).論大學(xué)數(shù)學(xué)教育改革[J].教育與職業(yè)，2007，（15）：141-142.

[2]李剛，張新敬.普通高校大學(xué)數(shù)學(xué)分層次教學(xué)探討[J].中州大學(xué)學(xué)報，2009，26（5）：98-99.

[3]劉明月.淺談大學(xué)數(shù)學(xué)的教學(xué)[J].學(xué)理論，2013，（36）：251-252.

[4]謝鳳英，趙丹培.Visual C++數(shù)字圖像處理[M].北京：電子工業(yè)出版社，2008.

[5]高峰修，張春元，馬智，等.工科研究生“矩陣論”課程教學(xué)研究[A].見：中國電子教育學(xué)會高教分會論文集[C].西安：中國電子教育學(xué)會高等教育分會，2012：90-92.endprint