數學類課程中“二三四”創新性教學模式初探

臧鴻雁

摘??要：在創新性人才培養的需求下，本文針對數學類課程，提出在課堂教學中挖掘知識產生過程，帶領學生重走前人創新之路，以及引領學生將所學知識延伸到專業領域的重要性。并以“概率論與數理統計”課程中的概率公理化定義和“信息理論基礎”課程中的事件信息量定義為例，闡述如何在課堂教學中引導學生挖掘數學定義產生過程，并以開放性作業為輔助和延伸，培養學生創新能力。經過三年的教學實踐，從學生的反饋來看，該方法在實踐中達到了良好的教學效果，尤其適合小班教學。

關鍵詞：數學類課程;創新性人才;概率公理化定義;信息量;開放性作業

2005年錢學森提出了一個令人深省的疑問：為什么我們的學校總是培養不出杰出人才？這一疑問，不僅成為社會各界對我國高等教育的疑問，而且成為建設創新型國家必須面對的疑問，更成為整個教育界及教育工作者對如何正確培養創新性人才的疑問。隨著“錢學森之問”在社會上引起的廣泛關注與討論，很多專家、學者分別在不同場合闡述了如何培養創新性人才的觀點。各高校特別是一些研究型高校，在創新性人才培養模式、理念等方面已經做出了努力，取得了顯著的成效。

高校教師在創新性人才成長中起著重要的作用，教師的教學理念和教學模式，將直接影響到創新性人才的培養質量。所以，積極探索創新性人才培養模式具有重要的意義。

一、數學類課程對創新性人才培養的重要性

基礎課程教學質量對創新性人才培養起著重要的作用。耶魯大學校長理查德·雷文在《美國大學是經濟發展的動力》演講中提出一個重要觀點：“基礎研究沒有明確的而實用的商業目的，而是完全以對知識的認識和探求為動力的。但基礎研究最終是具有商業導向的應用研究的和開發的源泉。時下正在進行的創新性商業產品的開發可能是依賴于10年、20?年或50年前基礎研究成果，而當時并不知道那些研究會有什么實用性結果。”?由于電子計算機的出現及飛速發展，作為基礎課程的數學類課程，正在以空前的廣度和深度向更多領域滲透。以數學為工具解決實際問題的模式如圖1所示。

圖1??數學解決實際問題模式

所以，數學類課程的教學改革對提高高校人才培養質量產生重要影響。

以考試為導向的傳統數學教學模式是課上注重知識點的講解，課下做大量習題鞏固知識點，這樣有助于培養知識儲備型人才，學生學過課程之后，會儲備豐富的該領域的知識。但是學生在數學課的學習中也表現出一些問題：知識點學習得很快，但考完試遺忘得也很快;課程的知識結構和研究思路不清晰;習慣跟著習題和試卷學習知識，不問知識產生的過程和意義;應試能力很強，特別在意分數，但研究問題能力有待提高;習慣照著做，不習慣問為什么這么做;習慣有人指導著做，不習慣主動去做;習慣一個人做，不習慣討論和合作。

基于以上問題，本文提出了數學類課程挖掘知識產生過程、構建數學知識、變知識傳承為思想傳承的教學理念。筆者在多年教學實踐中總結了一些具體措施和方法，并給出了一些具體的教學實施方案和教學效果的評價。

二、兩個對話

1.與創造知識的人對話

與創造知識的人對話，體現在課前備課階段。數學類課程歷史厚重，思想深刻。教材中往往匯集了幾百年來該學科發展過程中得到的重要理論和知識。比如很多數學定義本身是數學建模的過程，一個定義本身就是當時的重大創新成果。由于課堂學時受限，又有應試需求，所以絕大多數教材及課堂教學中對這些知識的產生過程沒有做出深入的挖掘，所以大多數學生對該課程中的一些重要知識的認識處于“只知其然而不知其所以然”的狀態。這樣，會導致在這門課程結束考試之后，知識的遺忘速度很快，在實際應用領域，又不知道如何學以致用。更重要的是因為知識產生過程的缺失，使得這樣培養的學生在該領域很難具有創造有價值的新知識的能力。所以，在備課的時候要對知識點產生過程進行研究，并且將其精華展現在課堂上，帶領學生重走前人創新之路，激發學生進一步研究的興趣，將進一步的深入研究引申到課外。這樣，有助于將數學課程的教學從知識傳承向思想傳承轉變。

挖掘知識產生的過程，對數學類課程的意義尤為重要。如果把獲得創新性的研究成果比喻成摘到果子，那么帶領同學們挖掘知識產生的過程，就猶如帶領同學們重現前人摘到果子的過程，重現在當時的條件下，前人如何克服困難找到解決問題的辦法，最后如何摘到了果子。如果在教學過程中，忽視這個環節，就相當于教師只是告訴學生這個果子是什么樣的，有多大，有多甜，如何食用。而在當今時代，也許果子更大，更紅，也更高了，而摘取果子所用的工具也更先進了，學習和借鑒前人解決問題的方法，才能在當前的環境下更好地解決現在的問題，獲得創新性的研究成果。

2.與學生對話

這部分屬于講授技巧的范疇，體現在課上及課后。一個優質的課堂必然是有感染力的，一個能吸引學生的教師必然是有親和力的。那么，感染力和親和力從哪里來呢？首先就是課堂內容的把握，邏輯嚴謹，有深度;其次就是教學環節的精心設計，用精美的課件把優秀的內容表現出來。如果以上兩點做得好，教師本身就會有強烈的想講的欲望，表現出來就是課堂的激情，這樣的課堂也就有了感染力。當然，課堂的主體是學生，交流和互動是非常重要的，如果這一點教學設計到位，教師做得好，教師就有了親和力。

另外，每位教師的授課都有自己的風格，這是由教師的性格決定的。有的和藹親切，有的不茍言笑，有的風趣幽默，有的言簡意賅，保持自己的風格并將之做到極致就是最好的。

三、三個境界

美國教育家肯·貝恩說過：僅僅憑借優雅的儀表、良好的愿望、悅耳洪亮的嗓音、熱情的目光交流——無論他們多么有用，還沒有達到教學的巔峰。大師級的老師不單單是優秀的講演家或討論的領導者;從根本上來講，他們應該是特殊類型的學者和思想家，引領自己和學生鉆研學問，享受智慧人生。對學生的關愛使他們注意表演的細節，他們的焦點定位在學習的本質和過程，而不是教師的表演[1]。

作為大學教師，對教學效果的追求是永無止境的，以下三個境界可以作為大學教師衡量自身教學能力的尺子。

1.優秀的講演家

教師首先就是要成為一個優秀的講演家，針對教學內容表達清晰，語言有感染力等，這是一個教師最起碼的能力。

2.優秀的組織者

教學過程畢竟不是講演，學生是課堂主體，所以教師要有效地調動學生思考，調動學生參與教學內容。這需要教師課前精心地進行課堂設計，課上有效地組織和調動學生。

3.優秀的思想家

教學過程不僅僅是傳授知識，教師也不僅僅擔負傳授知識的使命，還要傳承思想和方法。所以正如美國教育家肯·貝恩說的那樣，最優秀的教師應該是個學者和思想家。

四、四個問題

1.講什么

這部分的主要問題是課堂上如何利用有限的學時，簡短地呈現出所講知識點的精華部分。這部分重要的是要在課堂上構建知識，而不是灌輸知識。

傳統的數學類課程的教學模式，在課堂上重視知識點本身的講解，重視鞏固知識點的習題講解，這對培養知識儲備型人才是重要的。但這對培養創新性人才是遠遠不夠的。在課堂上對知識點產生的問題驅動及產生過程的研究以及知識點在應用領域的引申和研究都是重要的教學內容，對培養知識創新型人才和知識應用型人才具有重要意義。這些教學內容和人才培養類型之間的關系如圖2所示。

圖2??教學內容和人才培養類型之間的關系

2.怎么講

如何才能做到課堂上呈現精華，又如何引導學生重現前人創新過程，如何引導學生研究知識點在應用領域的延伸和提升呢？下面以“概率論與數理統計”課程中的概率公理化定義和“信息理論基礎”課程中的事件的信息量定義為例，闡述如何挖掘數學定義產生過程，從而培養學生創新能力。

（1）概率的公理化定義[2，3]

設E是隨機試驗，S是它的樣本空間，對于E的每一個事件A賦予一個實數，記為P（A），稱為事件A的概率，滿足下列條件：

對于這個定義，只要學生記住這三條，并且學會證明在此基礎上建立起的其他概率性質，會利用公理化的三條及其性質解題，知識層面的教學要求就基本達到了，學生的應試需求也就滿足了。但是，如果想還原當時的數學家的思想及解決問題的方法就必須澄清兩個問題：為什么要給這個公理化定義？公理化定義為什么是這樣三條？只有帶著這樣兩個問題去研究，才能將知識的傳承向思想和方法的傳承方面轉變。那么，在課堂教學中，就要簡短地介紹前人關于概率各種定義的嘗試，這些嘗試的意義及存在的問題。

①古典概率定義如下：

幾何概率19世紀被人們廣泛接受，直到1899年，法國數學家提出“貝特朗悖論”，使得該定義出現了邏輯上的自相矛盾。

③概率的統計定義：

在不變條件下，重復n次試驗，事件A發生的頻率穩定地在某一常數P?附近擺動，且一般說，n越大，擺動幅度越小，稱常數P為事件A?發生的概率，記P（A）。

統計定義只是描述性的，它刻畫了概率的存在性，無法用于進一步的計算和證明。

進一步分析，頻率穩定于概率并不能簡單地用極限式

來描述，而應該為

該式是用概率定義概率，在邏輯上是矛盾的。

基于上述原因，概率論需要完善自身的理論基礎。19世紀末，數學的其他分支，比如代數、幾何廣泛流行公理化熱潮，公理化是把基本概念性質假定成公理，其他結論由它們演繹導出。

1900年希爾伯特在巴黎國際數學家大會上的呼吁：把概率論公理化。由此，概率論公理化成為當時數學及整個自然科學的最迫切的問題之一。直到1933年，科爾莫戈羅夫出版了他的著作《概率論基礎》，給出了公理化概率論的一系列基本概念。

因為課堂學時受限，在概率公理化定義的講解過程中，不可能面面俱到，將其發展過程詳細講解，課上主要的任務是激發學生的研究興趣，很多詳盡的研究可以作為開放性的作業延伸到課堂之外。比如貝特朗悖論的內容是什么？比如在科爾莫戈羅夫提出現在被廣泛接受的公理化定義之前，其他數學家做過什么樣的嘗試？嘗試失敗的原因是什么？如果課堂上有了適當的引導和激發，學生的研究興趣還是很高的。

如果學生在研究的過程中遇到困難，教師需要適當引導和輔導。這對教師自身的能力要求是比較高的。

（2）事件的信息量的定義[4]

事件xi發生的概率為p（xi）

定義為xi的信息量。

該定義是1948年，信息論的創始人香農給出的，該定義是信息論這門學科的基礎。至于這個定義為什么是這樣一種形式，多數教材中并未提及，而這個定義的給出是當時的重大創新工作。因此，引導學生挖掘該定義的產生過程，對培養學生的創新能力有著重要意義。

首先，對于比較抽象的概念，要有直觀的感受，從心理學認知角度來講，信息是有大小之分，一個很少發生的事情當突然發生時，給人的沖擊是很大的;反之，經常發生的事情則給人的印象是很淡的。這點很容易理解，比如人們總是津津樂道于小概率事件，小概率事件的發生通常都有大量原因的積累，而小概率事件背后一定有大量的新聞。還有一點也很直觀，就是如果兩個事件相互獨立，那么它們的積事件所包含的信息量應該是各自所包含的信息量之和。認識到這兩點，就可以建立事件的信息量的數學模型了。建立數學模型是希望能找到一個關于概率的函數，滿足非負性、單調性、可加性、連續性。數學上可以證明，滿足以上四個條件的函數是唯一存在的，那就是

香農給的信息量的定義也就順理成章地被推出來了。這樣，這個知識就被構建出來了。當然，證明過程詳盡的研究可以延伸到課堂之外，由開放性作業的形式加以補充。

以上僅以兩例闡述如何引導學生挖掘數學定義產生過程，重走前人創新之路。另外，引導學生將知識點在應用領域進行提升也很重要。在這兩個過程中，會遇到如下問題：一是還原思想歷程有時是困難的。經過幾百年以后，后代的數學家就都把前人的理論詮釋修改，變成了一系列的定理、公理、推論，有時完全看不出前人當時的思想歷程。二是應用領域的提升知識點對教師的實際科學研究經歷要求較高。直接講解知識相對比較容易，只有站得高才能真正靈活駕馭知識點。

這部分課堂上呈現知識點的產生過程和應用領域的提升要盡可能地簡短。課堂上的主要任務是提出一些具有啟發性的問題，激發學生進一步研究的興趣，布置開放性作業，將進一步的研究延伸到課外。

3.怎么學

學生的學習方法要與教師的教學方法相匹配，做到相互配合，以達到提高數學思維方法、提高應用數學解決實際問題能力的目的。學生以問題為導向的研究型學習方法為主，以試卷為導向的應試學習方法為輔。對課后習題，放棄習題解答，習慣獨立思考獨立解決問題。與習題的正確答案相比，探索正確答案的過程中積累的經驗和教訓更重要。另外學生要重視開放性作業的研究，這樣教師的教學方法才能產生效果。

4.怎么考

學生對分數還是相當重視的，因為分數直接影響學生以后的去向。所以，在考核環節，要加強試卷以外的過程成績的管理，尤其是開放性作業的成績評定。要想調動學生研究開放性作業的積極性，就必須研究如何公平合理地給出開放性作業的成績。

關于開放性作業，有以下幾個環節需要考慮。

（1）開放性作業題目的選擇。開放性作業的內容基本上是無法落實在考試卷上的研究性題目，作為提高學生綜合素質、提高解決實際問題能力的有益補充。比如課上知識點補充、引申思考問題或證明、知識點產生過程的挖掘、知識點在應用領域的延伸和提升等。選擇題目的時候要注意難易適中，太難的題目容易打擊學生的研究積極性。另外，允許學生在一定范圍內選擇自己感興趣的題目。

（2）開放性作業所占分數比例。開放性作業成績所占總成績的比例要適當。開放性作業成績所占總成績的比例不能太低，太低不能充分調動學生投入的積極性。因為教師難以掌握學生開放性作業細節問題，做到十分公正地給出成績，所以如果開放性作業成績所占比例太高，容易引起學生的不滿。筆者的經驗是：10%的比例不能引起學生的充分重視，20%的比例開放性作業質量明顯提升。

（3）開放性作業完成小組人數。開放性作業通常工作量比較大，比較適合幾位同學組成小組，合作完成。同時，小組成員合作完成開放性作業的形式也有助于培養學生的團隊合作能力。小組人數太多，容易任務不清，出現互相推諉等問題。筆者的經驗是：小組人數不要超過3人。

（4）開放性作業打分和反饋交流。開放性作業的反饋交流是比較困難的一個環節，主要是因為通常數學類課程課堂人數比較多，開放性作業的反饋和交流就要占用很多的時間，尤其是針對研究生考試必考的科目，比如概率論與數理統計，開放性作業的交流占用很多的時間是不現實的。如果僅僅是開放性作業的匯報則相對容易一些，可以給每個小組固定的時間，展示一下自己的作業成果。

比較客觀地給出開放性作業的分數也很重要。困難在于組內成員的分數有時難以評定，教師很難全面了解組內的分工和組內成員的實際貢獻。如果有充分的時間與每組進行充分的交流，交流的過程中能夠看出小組各位同學的貢獻。但是，如果學生人數太多，教師要做到與每組都有充分交流是十分困難的事情。如果教師做不到與每組都有充分交流，就要求學生開放性作業的報告中寫清楚組內各成員的分工情況，并要求組內的同學互相打分，作為教師給分的主要參考。

五、學生反饋

1.學生抽樣調查結果

對2013—2014年第一學期會計專業112位學生進行了抽樣調查，共回收有效問卷96份，覺得開放性作業收獲很大的占33/96，收獲較大47/96，收獲一般的占15/96，沒什么收獲的占1/96。

在開放性作業所占比例環節，有64/96贊成開放性作業所占比例由10%增加至20%，有18/96反對，14/96認為無所謂。

2.學生滿意度分析

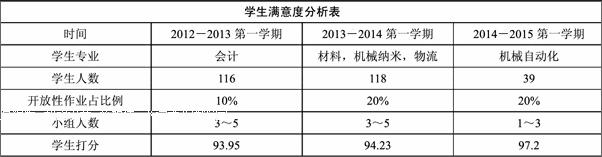
針對概率論與數理統計課程，筆者連續3年按照前面所述的教學理念和措施進行教學實踐。面對不同專業，不同的講臺人數，選取不同的開放性作業比例，學生對教師滿意度情況見下表。

學生滿意度分析表

由上表的結果可見，當學生人數較少，相應的開放性作業小組人數也較少時，這種教學方式能夠得到學生更高程度的認可。

參考文獻：

[1]?[美]肯·貝恩.?如何成為卓越的大學教師[M].?北京：北京大學出版社，2007.

[2]?蘇淳.?概率論[M].?北京：科學出版社，2004.

[3]?陳希儒.?概率統計學簡史[M].?長沙：湖南教育出版社，1998.

[4]?C.?E.?Shannon.?A?Mathematical?Theory?of?Communication[J].?The?Bell?System?Technical?Journal，?1948（27）：379-423，?623-656.

[本文為北京市人才培養共建項目-教育教學項目-教育教學改革項目（GJ201415）和北京科技大學2013青年教學骨干人才項目（06200016）階段性成果]

[責任編輯：余大品]